FIR滤波器基本网络结构 G则是整个系统归一化的增益。 可以看出,这个函数是适用于IIR系统的,因为 它同时把分子分母都进行了因式分解。使用于 FIR系统时,只要把a用1代入即可。 例如键入:[sos,G]=tf2sos([0.9622.81.5],1),得到 s0s=1.0000 0.8333 0 1.0000 0 0 1.0000 1.2500 1.8750 1.0000 0 0 G=0.9600 系统函数与前面手工计算的结果相同。为: H(z)=0.961+0.8333z1)1+1.25z1+1.875z2) 26
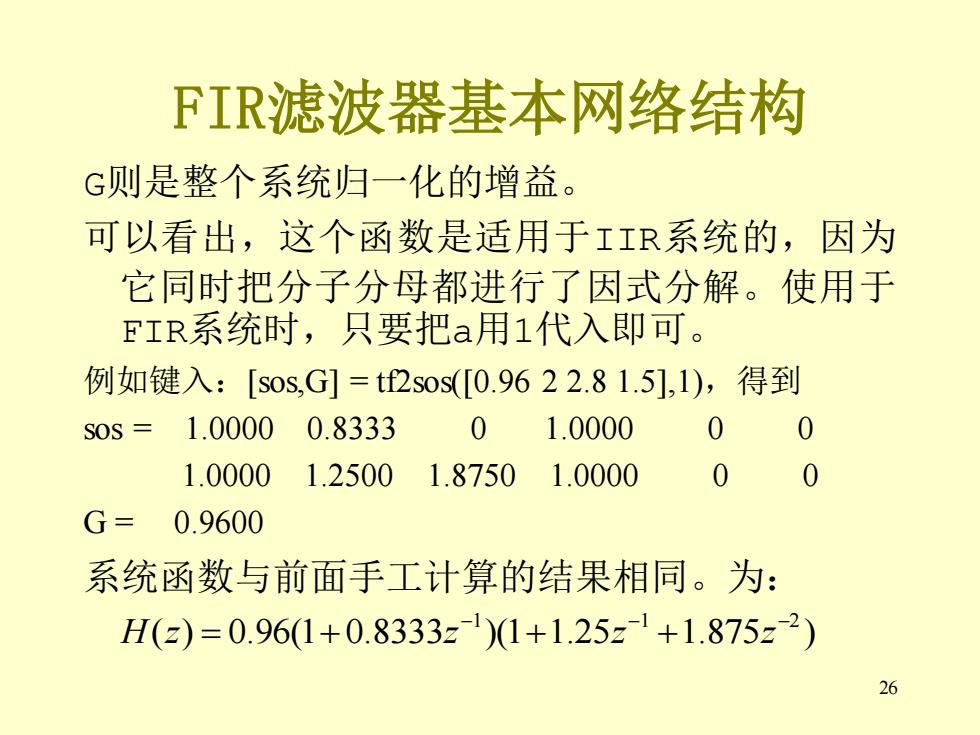
26 FIR滤波器基本网络结构 G则是整个系统归一化的增益。 可以看出,这个函数是适用于IIR系统的,因为 它同时把分子分母都进行了因式分解。使用于 FIR系统时,只要把a用1代入即可。 例如键入:[sos,G] = tf2sos([0.96 2 2.8 1.5],1),得到 sos = 1.0000 0.8333 0 1.0000 0 0 1.0000 1.2500 1.8750 1.0000 0 0 G = 0.9600 系统函数与前面手工计算的结果相同。为: 1 1 2 H z z z z ( ) 0.96(1 0.8333 )(1 1.25 1.875 ) − − − = + + +

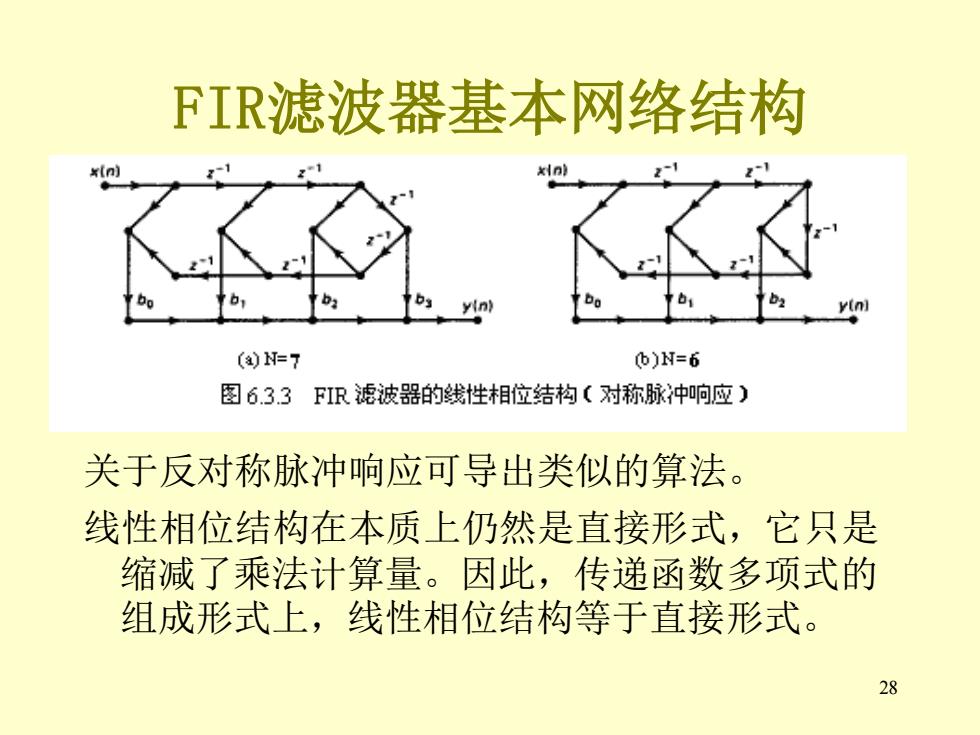
FIR滤波器基本网络结构 线性相位结构:上章指出,线性相位滤波器的脉 冲响应序列,因而其系数应当具有对称性。可 以是对称结构,也可以是反对称结构。 若差分方程具有(6.3.10)中的对称脉冲响应。 可以将对称项结合,共用系数,得到 y(n)=box(n)+b1x(n-1)+...+bN=1x(n-N+1) =bo[x(n)+x(n-N+1]+b[x(n-1)+x(n-N+2]+… 图6.3.3表示了N为奇数和偶数两种情况下实现上 述方程的方框图。系数和乘法都减少一半 27
27 FIR滤波器基本网络结构 线性相位结构:上章指出,线性相位滤波器的脉 冲响应序列,因而其系数应当具有对称性。可 以是对称结构,也可以是反对称结构。 若差分方程具有(6.3.10)中的对称脉冲响应。 可以将对称项结合,共用系数,得到 图6.3.3表示了N为奇数和偶数两种情况下实现上 述方程的方框图。系数和乘法都减少一半 = + − + + − + − + + = + − + + − − + [ ( ) ( 1)] [ ( 1) ( 2)] ( ) ( ) ( 1) ( 1) 0 1 0 1 1 b x n x n N b x n x n N y n b x n b x n b N x n N
FIR滤波器基本网络结构 ()N=7 b)W=6 图6.3.3FIR滤波器的线性相位结构(对称脉冲响应) 关于反对称脉冲响应可导出类似的算法。 线性相位结构在本质上仍然是直接形式,它只是 缩减了乘法计算量。因此,传递函数多项式的 组成形式上,线性相位结构等于直接形式。 28
28 FIR滤波器基本网络结构 关于反对称脉冲响应可导出类似的算法。 线性相位结构在本质上仍然是直接形式,它只是 缩减了乘法计算量。因此,传递函数多项式的 组成形式上,线性相位结构等于直接形式

FIR滤波器基本网络结构 例6.3.2设FR滤波器由下列系统函数给定 H(z)=1+16.0625z4+z-8 求出并画出它的直接形式、线性相位形式和级联 形式结构。 解:a.直接形式:差分方程可写为: y(n)=x(n)+16.0625x(n-4)+x(n-8) 直接形式结构如图6.3.4(a)所示。 29
29 FIR滤波器基本网络结构 例6.3.2 设FIR滤波器由下列系统函数给定 求出并画出它的直接形式、线性相位形式和级联 形式结构。 解:a. 直接形式:差分方程可写为: 直接形式结构如图6.3.4(a)所示。 4 8 ( ) 1 16.0625 − − H z = + z + z y(n) = x(n) +16.0625x(n − 4) + x(n − 8)

FIR滤波器基本网络结构 b.线性相位形式:差分方程可写为: y(n)=[x(n)+x(n-8)]+16.0625x(n-4) 所得结构如图6.3.4(b)所示。 C.级联形式:用MATLAB协助,键入 b=[1,0,0,0,16.0625,0,0,0,1]: [sos,G]=tf2sos(b,1) 程序运行的结果为: 30
30 FIR滤波器基本网络结构 b. 线性相位形式:差分方程可写为: 所得结构如图6.3.4(b)所示。 c. .级联形式:用MATLAB协助,键入 b=[1,0,0,0,16.0625,0,0,0,1]; [sos,G]=tf2sos(b,1) 程序运行的结果为: y(n) = [x(n) + x(n − 8)] +16.0625x(n − 4)