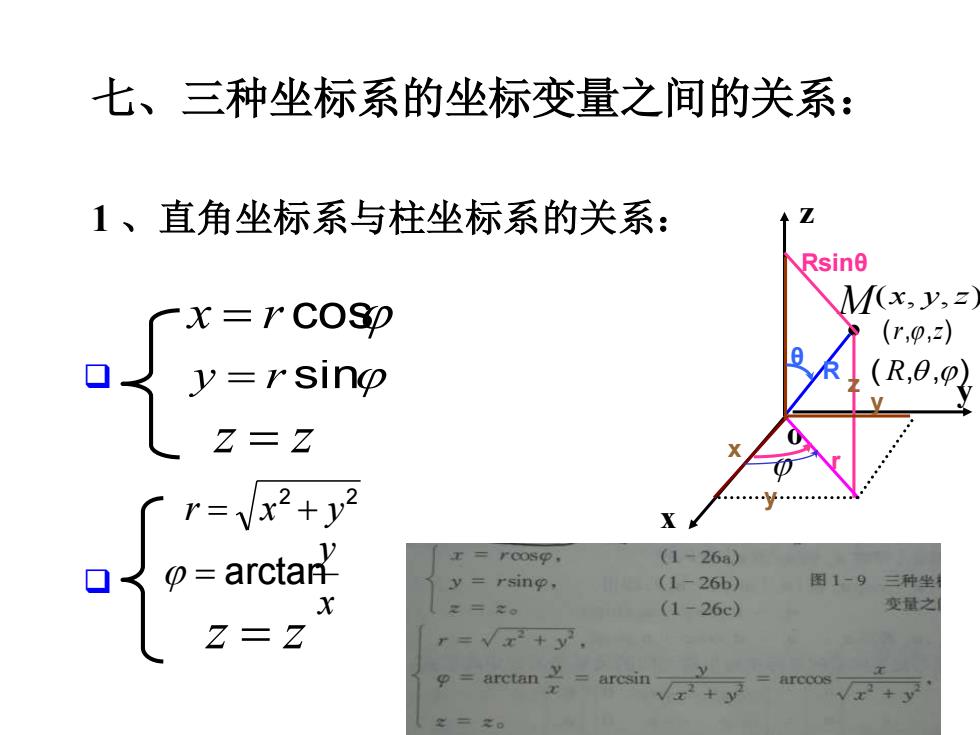
七、三种坐标系的坐标变量之间的关系:Z1、直角坐标系与柱坐标系的关系:RsineM(x, y,z)x=rcosD(r,p,z)(R,0,p)口y=rsinpZ=Z(1-268)rCosβ= arctan口图1-9三种坐(1-26b)=rsingx变量之(1-26c)z=z++
( , , ) x y z 七、三种坐标系的坐标变量之间的关系: 1 、直角坐标系与柱坐标系的关系: y = r sin x = r cos z = z ❑ ❑ 2 2 r = x + y x y = arctan z = z y ( R, ,) x o M (r,,z) r R θ x y z Rsinθ z y
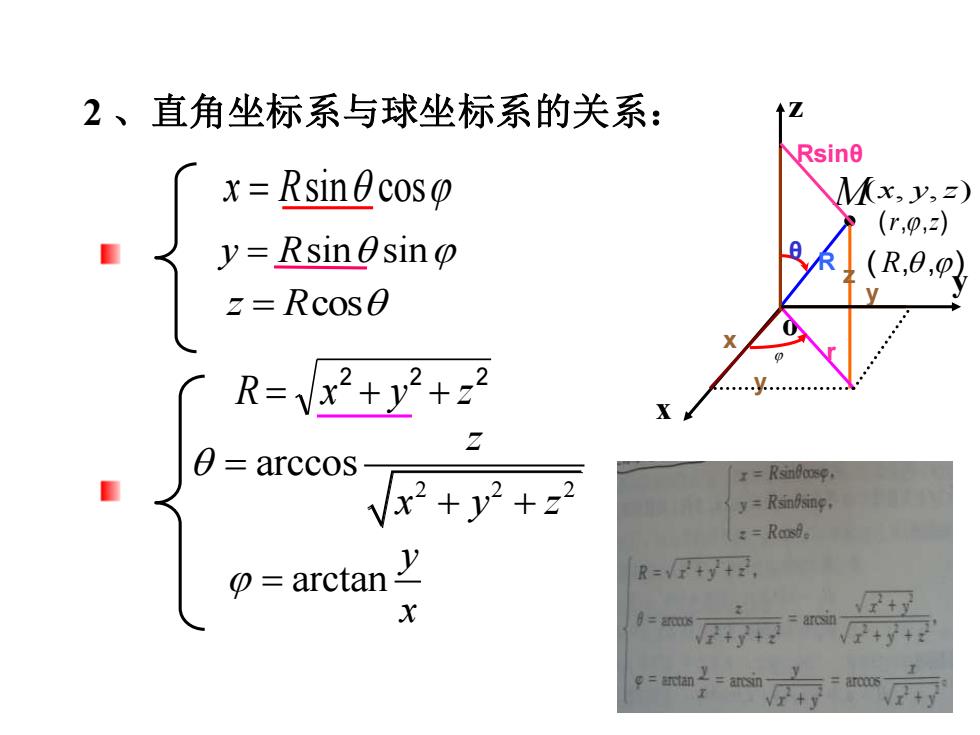
2、直角坐标系与球坐标系的关系:12Rsinex = RsincospMx, y,z)(r,p,z)y=Rsinsin@(R,0,p)Vz= Rcos022Z1=arccos1=Rsinfoosey=RsinBsing,2=RonsfeyR=/P+y+?@ = arctan +xP+V+2NI+++?三atar=arcooVP+V十
2 2 2 R = x + y + z arctan y x = 2 2 2 arccos z x y z = + + 2 、直角坐标系与球坐标系的关系: y ( , , ) x y z y ( R, ,) x o M (r,,z) r R θ x y z Rsinθ z y R = sin sin x R = sin cos z R= cos
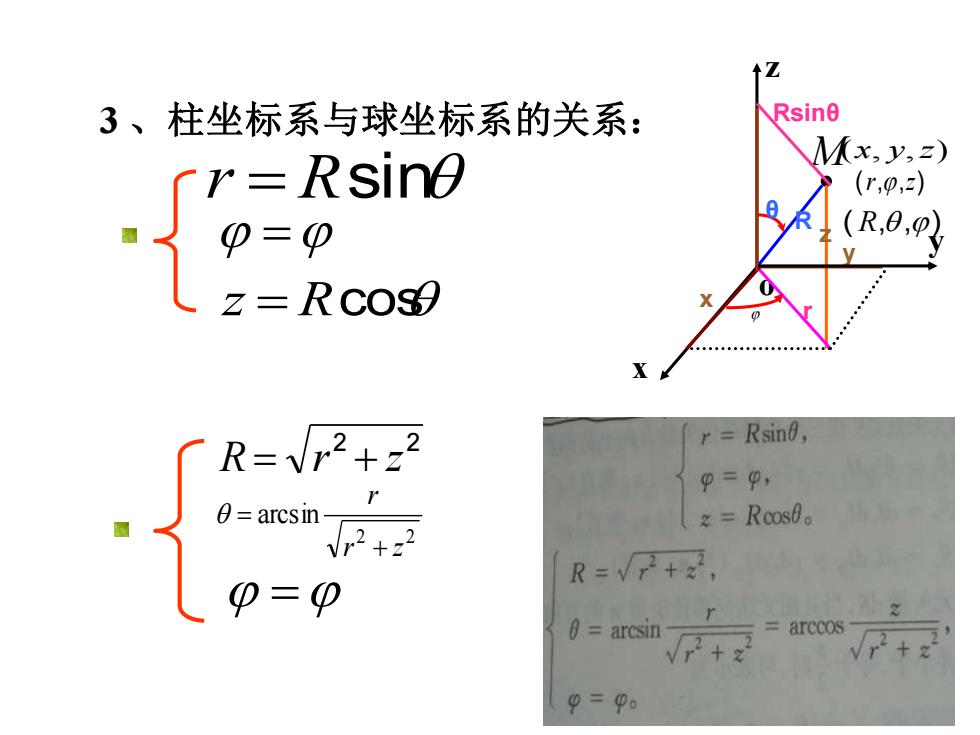
1zRsine3、柱坐标系与球坐标系的关系:Mx,y,z)r = Rsino(r,p,z2)D(R,0,p)=Φz = Rco$r=Rsing,2R=9=,72=Rcos。0= arcsinVr.2+z2R=V2+2,Φ=@@=arcsinarccos2+89=9
r = Rsin = z = Rcos 2 2 arcsin r z r + = 2 2 R = r + z = 3 、柱坐标系与球坐标系的关系: ( , , ) x y z y ( R, ,) x o M (r,,z) r R θ x y z Rsinθ z
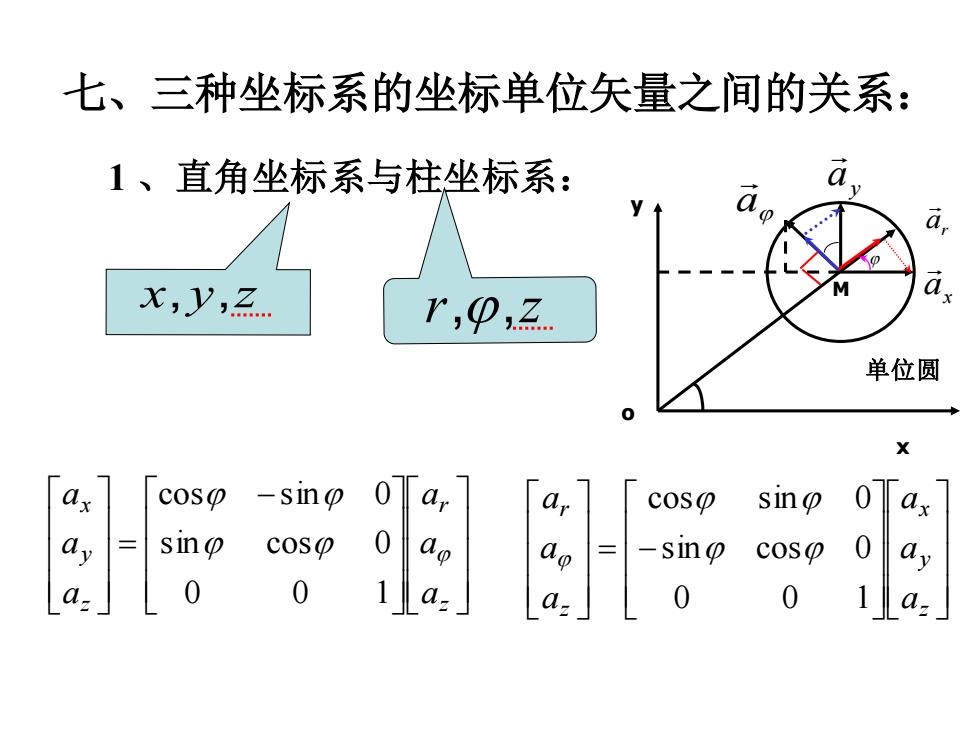
七、三种坐标系的坐标单位矢量之间的关系:a1、直角坐标系与柱坐标系:aa.a2X,y,z.r,O,z.单位圆x0cosp-sinparasinp0cos@ar?0sing0cos@ayapsin@cos@aoay0000aa.a.a
七、三种坐标系的坐标单位矢量之间的关系: 1 、直角坐标系与柱坐标系: r,,z x, y,z x M o y 单位圆 ax ar ay a − = z r z y x a a a a a a 0 0 1 sin cos 0 cos sin 0 = − z y x z r a a a a a a 0 0 1 sin cos 0 cos sin 0

2、柱坐标系与球坐标系的关系:00singcos0sin0cos0ara,aRaR0010apcos-sinaeapae二0cose-sino100Lazlaz3、直角坐标系与球坐标系:aRcosOsincosp sinsinpaxcosocosp cososinp-sinoagay/0-sindcospapazsingcospcosacosp-sin0axaRsindsinpcosasin pcosayao0cosO-sindapaz
2 、柱坐标系与球坐标系的关系: 3、 直角坐标系与球坐标系: − = a a a a a a R z r cos sin 0 0 0 1 sin cos 0 = − z R r a a a a a a 0 1 0 cos 0 sin sin 0 cos − = − z y R x a a a a a a sin cos 0 cos cos cos sin sin sin cos sin sin cos − − = a a a a a a R z y x cos sin 0 sin sin cos sin cos sin cos cos cos sin