《电磁场与电磁能》课程PPT教学课件（马冰然版）第二章 静电场 2.5 泊松方程和拉普拉斯方程

第二章2.52.5泊松方程和拉普拉斯方程牛 静电巧的基本方程：线性、均匀、各向同性电介质fE.di -0无旋：积C分fD.ds =q有散V×E=0微分V.D=p本构关系D==,=+P2025/6/11

2025/6/11 第二章 2.5 1 2.5 泊松方程和拉普拉斯方程 静电场的基本方程: 线性、均匀、各向同性 电介质     =  = s c D ds q E dl     0 积 分 无旋： 有散  =   = D E   0 微 分 本构关系： D E r E E P      =  =  0  =  0 +

第二章2.5泊松方程和拉普拉斯方程：正泊松方程：X：静电场为无旋场，故可引入Φ标量电位来描述之。而V.D=p将D= 及 E=-VΦ 代入上式中V.sE=pV.E-P即8d泊松方程V.Ve=-P8(2-5-1)P822025/6/11

2025/6/11 第二章 2.5 2 泊松方程和拉普拉斯方程： ❖ 泊松方程： ∵ 静电场为无旋场，故可引入一标量电位  来描述之。 而  D =   将 D = E 及 E = − 代入上式中    即            = −  = −  =  = 2 E E   （2-5-1）  的泊松方程

第二章2.5拉普拉斯方程X若静电场中无电荷分布时，即β=0D的拉普拉斯方程2Φ=0V2则泊松方程为：(2-5-2)拉普拉斯算符√2：XV?=V.V标量算符32025/6/11

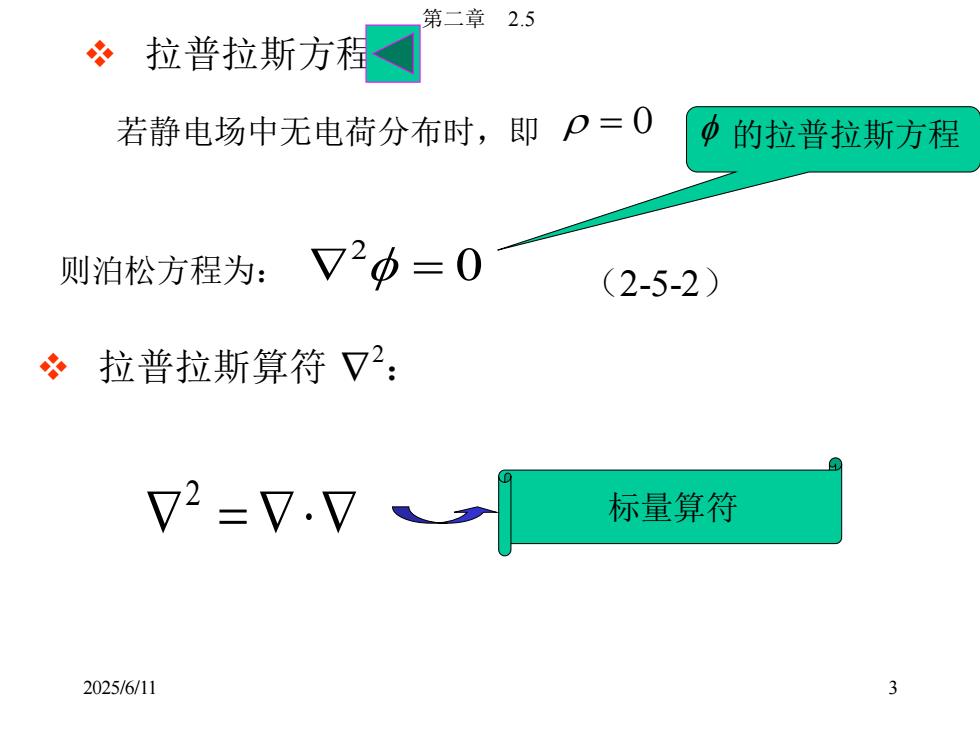
2025/6/11 第二章 2.5 3 ❖ 拉普拉斯方程： 若静电场中无电荷分布时，即  = 0 则泊松方程为： 0 2   = （2-5-2）  的拉普拉斯方程 ❖ 拉普拉斯算符  2 ：  =  2 标量算符

第二章25拉普拉斯算符在各坐标系中的表示式：a?aa?p直角坐标系：Oy2Qz2Ox?柱坐标系：1 aaa~dOrQz2aor OrF球坐标系：1a1adadadCsinaOrOra0sin?0 p4sin00042025/6/11

2025/6/11 第二章 2.5 4 ❖ 拉普拉斯算符在各坐标系中的表示式： 直角坐标系： 2 2 2 2 2 2 2 x y z  +   +    =     柱坐标系： 2 2 2 2 2 2 1 ( ) 1 r r z r r r   +   +      =      球坐标系： 2 2 2 2 2 2 2 2 1 1 1 ( ) (sin ) sin sin r r r r r r                 = + +     

第二章2.5求解泊松方程（或拉普拉X斯方程）：Φ=E给定电荷分布，求解其方程得(:E=-VΦ)若已知E、D→ p2025/6/11

2025/6/11 第二章 2.5 5 ❖ 求解泊松方程（或拉普拉 斯方程）： 给定电荷分布，求解其方程得 E    若已知 E D 、   （ ） E = −