
悬链线(The Catenary) 假设悬线自由悬挂,只考虑自身重量,此时曲线的形状: y=cosha(x+C)+C:= a(xC)te-a(xCi) +C2 a 2a 提示: V(x+△)-()=Y:△,人、H为张力的垂直分量和水平分量, H(x+△x)=H(x), y为单位长细线所受重力。由中值定理并令△x→0得到V(x)=ys, 利用y'(x)= 得到(ye-r)=y盘=W+0 ds H(x) 考虑到H(x)=H 04f P y元+6T=ai+07 y(x)=,(x2)=2 y=y(x)
悬链线(The Catenary) 1 1 ( 1 2 ) ( ) 2 1 cosh ( : 2 ) a x C a x C y a x C C e e C a a 假设悬线自由悬挂,只考虑自身重量,此时曲线的形状: 2 0 2 2 1 1 2 0 2 ( ) ( ) 1 ( ) ( ) 1 ( ) ( ) ( ) ( ), 0 ( ) , ( ) ( ( ) 1 ( ) ( ) , ( ) ( ) ) ( ) x H x y x y x H x H y y y y x y V x x V x s V H H x x H x x V x s V x ds y x V x H x dx x y a H y , 提示: , 、 为张力的垂直分量和水平分量, 为单位长细线所受重力。由中值定理并令 得到 利用 得到 考虑到
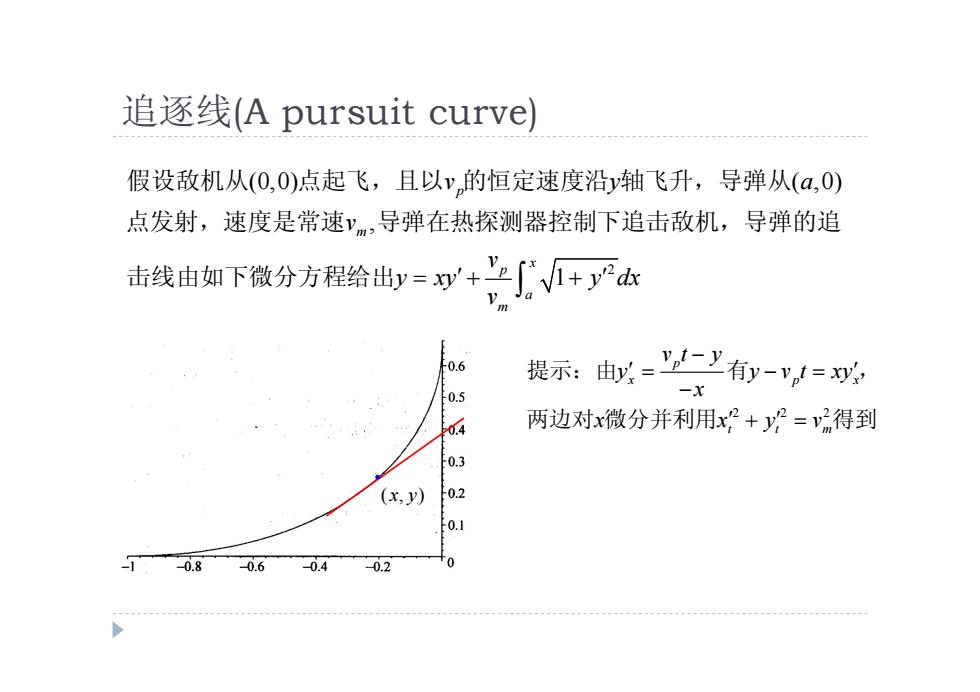
追逐线(A pursuit curve) 假设敌机从(0,0)点起飞,且以y,的恒定速度沿轴飞升,导弹从(a,0) 点发射,速度是常速ym,导弹在热探测器控制下追击敌机,导弹的追 击线由如下微分方程给出y=+∫+少 0.6 提示:y='二y有y-v= 0.5 -x 04 两边对x微分并利用x+2=v2得到 0.3 (x,y) 0.2 0.1 -0.8 0.6 -0.4 0.2 0
追逐线(A pursuit curve) 2 (0,0) ( ,0) , 1 p m x p a m v y a v v y xy y dx v 假设敌机从 点起飞,且以 的恒定速度沿 轴飞升,导弹从 点发射,速度是常速 导弹在热探测器控制下追击敌机,导弹的追 击线由如下微分方程给出 2 2 2 p x p x t t m v t y y y v t xy x x x y v 提示:由 有 , 两边对 微分并利用 得到 ( , ) x y
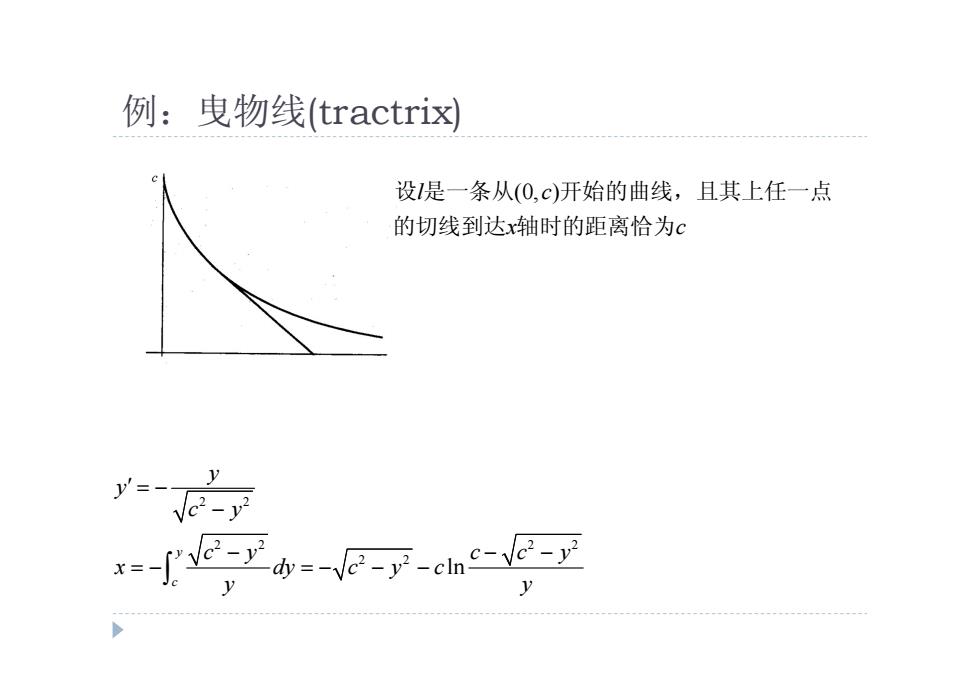
例:曳物线(tractrix) 设是一条从(0,c)开始的曲线,且其上任一点 的切线到达x轴时的距离恰为c y--Je-y x小=e-y-ch-y
例:曳物线(tractrix) 2 2 2 2 2 2 2 2 ln y c y y c y c y c c y x dy c y c y y l c (0, ) x c 设 是一条从 开始的曲线,且其上任一点 的切线到达 轴时的距离恰为
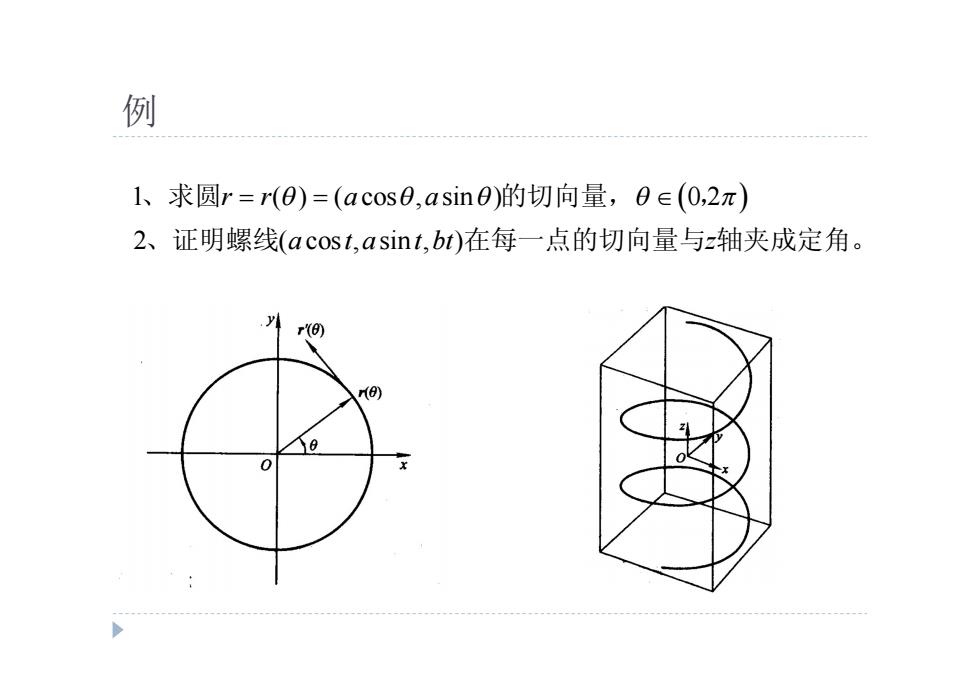
例 1、求圆r=r(0)=(acos0,asin0)的切向量,0∈(0,2π) 2、证明螺线(acost,.asint,,bt)在每一点的切向量与z轴夹成定角。 r(e) re)
例 1 ( ) ( cos , sin ) 0 2 2 ( cos , sin , ) r r a a a t a t bt z 、求圆 的切向量, , 、证明螺线 在每一点的切向量与 轴夹成定角
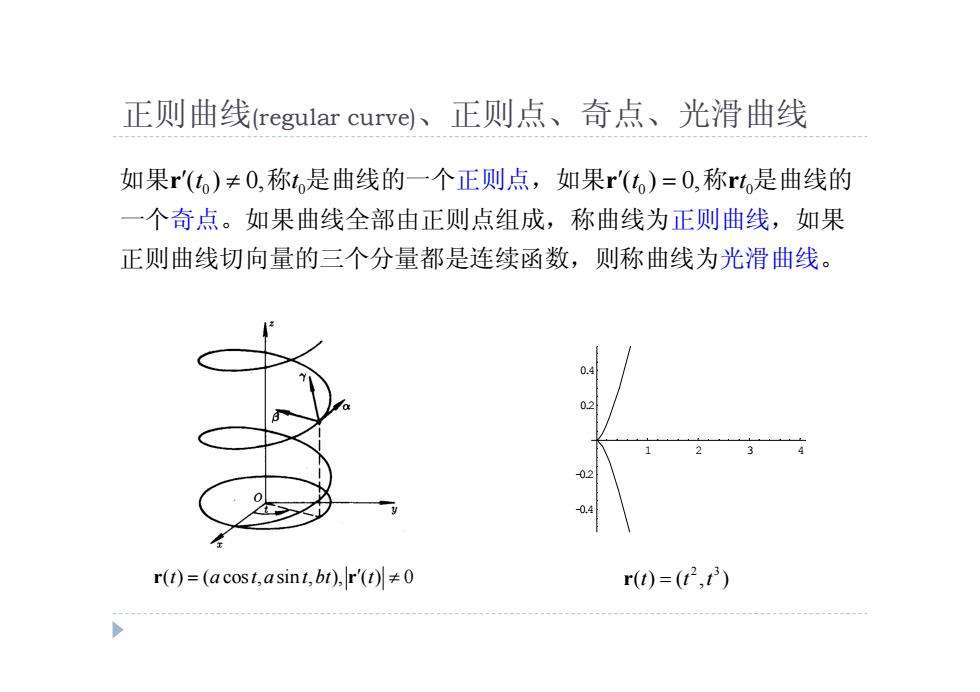
正则曲线regular curve)、正则点、奇点、光滑曲线 如果r'(t)≠0,称t,是曲线的一个正则点,如果r'(t)=0,称rt,是曲线的 一个奇点。如果曲线全部由正则点组成,称曲线为正则曲线,如果 正则曲线切向量的三个分量都是连续函数,则称曲线为光滑曲线。 0.4 02 0 r(t)=(acost,asint,bt),r'(t)0 r)=(t2,t)
正则曲线(regular curve)、正则点、奇点、光滑曲线 0 0 0 0 如果r r r ( ) 0, ( ) 0, t t t t 称 是曲线的一个 ,如果 称 是曲线的 一个 。如果曲线全部由正则点组成,称曲线为 ,如果 正则曲线切向量的三个分量都是连续函数,则称 正则点 奇点 正 曲线为 则曲线 光滑曲线。 1 2 3 4 -0.4 -0.2 0.2 0.4 2 3 r r ( ) ( cos , sin , ), ( ) 0 t a t a t bt t r( ) ( , ) t t t