函数的积分
函数的积分
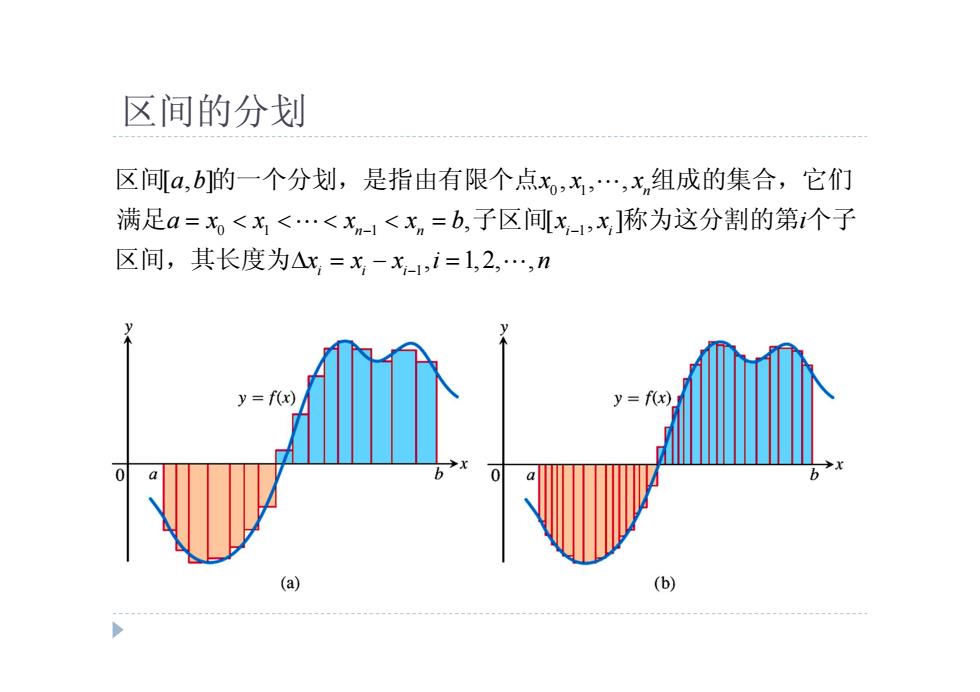
区间的分划 区间[a,b的一个分划,是指由有限个点x,x,…,x,组成的集合,它们 满足a=x<x<<x-1<,=b,子区间[x-1,x]称为这分割的第个子 区间,其长度为△x,=x,-x-,i=1,2,…,n y=f(x) y=f(x) 0 b 0 b (a) (b)
区间的分划 0 1 0 1 1 1 1 [ , ] , , , , [ , ] , 1, 2, , n n n i i i i i a b x x x a x x x x b x x i x x x i n 区间 的一个分划,是指由有限个点 组成的集合,它们 满足 子区间 称为这分割的第 个子 区间,其长度为
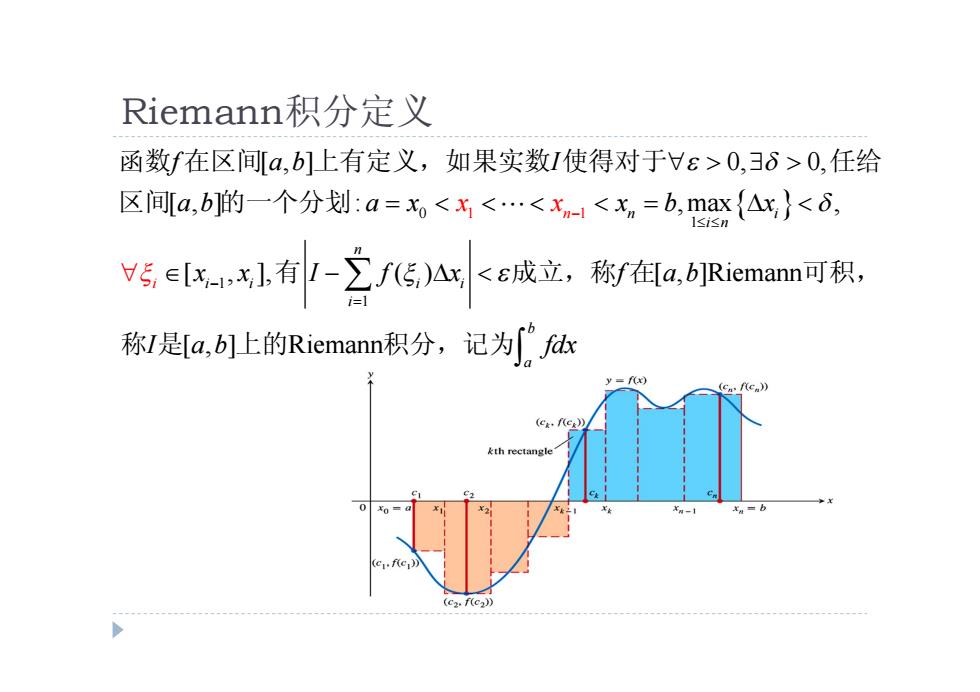
Riemann积分定义 函数f在区间[a,b]上有定义,如果实数I使得对于Vε>0,δ>0,任给 区间[a,b]的一个分划:a=x<x<…<xn-1<x,=b,max{Ax}<d, V发ck1有-立GA<e成立,称.Riemamt可积, 称I是[a,b]上的Riemann积分,记为fr =x c.(C kth rectangl (cfc2》
Riemann积分定义 0 1 1 1 1 1 [ , ] 0, 0, [ , ] : ,max , [ , ], ( ) [ , ]Riemann [ , ] Riemann n i i n n i i i i i i b a n f a b I a b a x x b x x x I f x f a b I a dx x x b f 函数 在区间 上有定义,如果实数 使得对于 任给 区间 的一个分划 有 成立,称 在 可积, 称 是 上的 积分,记为

可积函数的有界性 f在[a,b]可积,则f在[a,b]有界 取=l,存在分划△:a=x<x<<x-1<xn=b,5,∈[xX,] 满足:1-立A<1,即它八A<川+L进而有 sX<+1+2G数G+1+空G 固定5,i=2,3,,n,立即得到f在[x,x]区间上的有界性,同理可得 在[x-x,](i=2,3,…,n)区间上的有界性,从而得到f的有界性
可积函数的有界性 f a b f a b 在[ , ] [ , ] 可积,则 在 有界 0 1 1 1 1 1 1 1 1 2 2 1 0 1 1 =1 , [ , ], ( ) 1 ( ) 1, 1 ( ) 1 ( ) , ( ) 1 ( ) , , 2,3, , , [ , ] [ , n n i i i n n i i i i i i n n i i i i i i i i i a x x x x b x x I f x f x I f x I f x f I f x x i n f x x f x x 取 ,存在分划 : 满足: ,即 进而有 故 固定 立即得到 在 区间上的有界性,同理可得 在 ] 2,3, , i n f 区间上的有界性,从而得到 的有界性

函数的振幅、Darboux上和、下和 给定区间[a,b]和定义在其上的有界函数f(x),f在[a,b]上的上下确界分别 为M,m,令o=M-m称为f在[a,b]区间上的振幅 给定区间[a,b的一个分割△:a=x。<x<…<xn1<xn=b,在每个子区间 [x-,x]上f的上下确界分别记为M,m,并令o,=M,-m,称之为f在子区间 [xx止的振幅,定义5=∑MAx,S=∑mAx 份别称为f关于分割△ 的Darboux.上和Darboux下和
函数的振幅、Darboux上和、下和 0 1 1 1 1 1 1 [ , ] ( ) [ , ] , , [ , ] [ , ] , [ , ] , , [ , ] , n n i i i i i n n i i i i i i i i i i a b f x f a b M m f a b a b a x x x x b x x f M m M m f x M m x f S M x S m x 给定区间 和定义在其上的有界函数 , 在 上的上下确界分别 为 令 称为 在 区间上的振幅 给定区间 的一个分割 : 在每个子区间 上 的上下确界分别记为 并令 称之为 在子区间 上的振幅,定义 分别称为 关于 Darboux Darboux 分割 的 上和 下和