例 求解常微分方程: y 1 =y2+ (Riccati) dx y0x=2+12/2 令 代入方程得到 SolutionEul y Step size:D.1 会1 Plot color:Red ntial condtions 0=093932 =1.370 得到通解 Plot solution // Solve equation y=1 /y121-ta12iog+12℃ 1
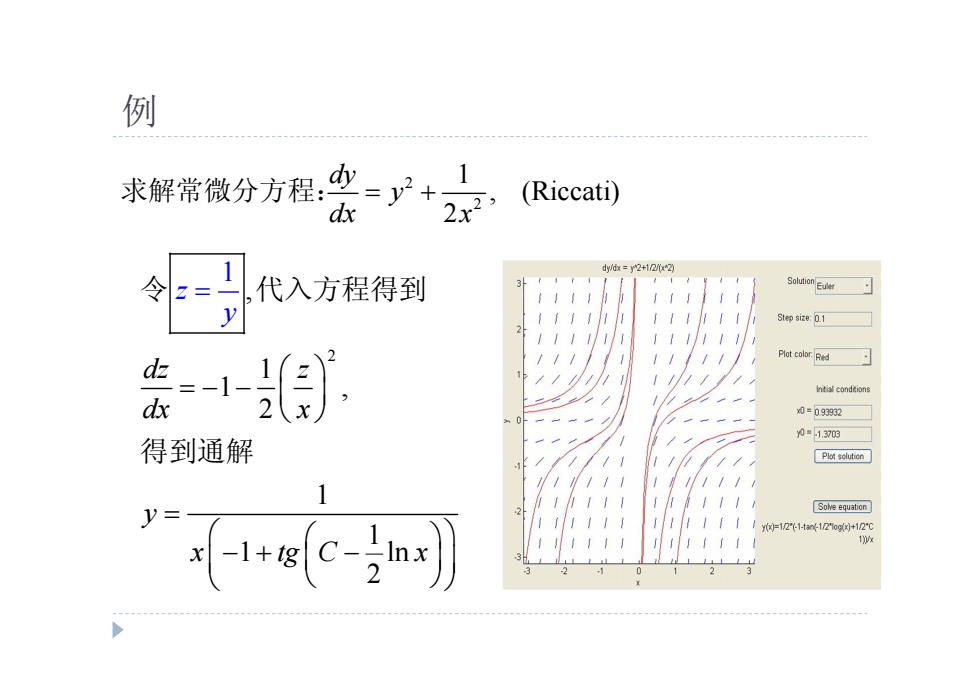
例 2 2 1 , (Riccati) 2 dy y dx x 求解常微分方程: 2 , 1 1 , 2 1 1 1 ln 2 1 dz z dx x z y y x tg C x 令 代入方程得到 得到通解
例 求解常微分方程: =y2+x2 dx dv/dx =x2+2 Solution Euler Step size:0.1 Piot color Red nitial condition ×0=0.02368 y0=0.014578 Plot solution Solve equation] y00=(C1b0sse3/4,12x2+地 ssely(3/4.1/2*x2))x/(C1"b "x2)
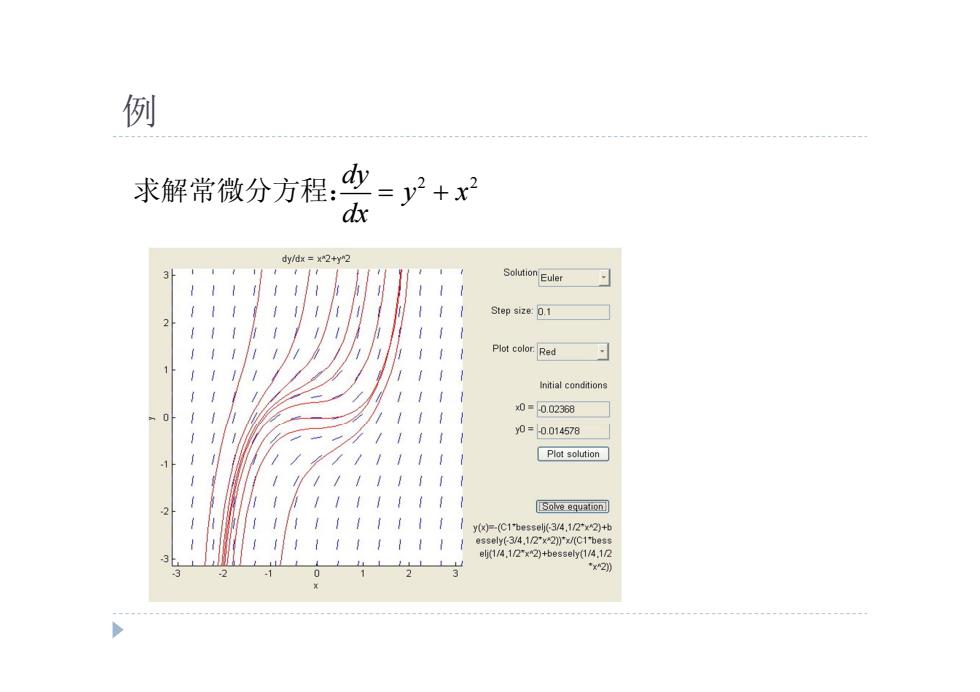
例 dy 2 2 y x dx 求解常微分方程:
空间曲线和空间曲线上的向量场 r(t)=x(t)i+y(t)j+z(t)k,(a≤t≤b)为一空间曲线的参数化形式,从几何 的观点看,此曲线由点{(x(),y),()a≤t≤b}组成 考虑一个任意向量场F(x,y,z),并将其限制在我们的空间曲线上,即向 量F(x(t),yt),z(t) 空间曲线Y
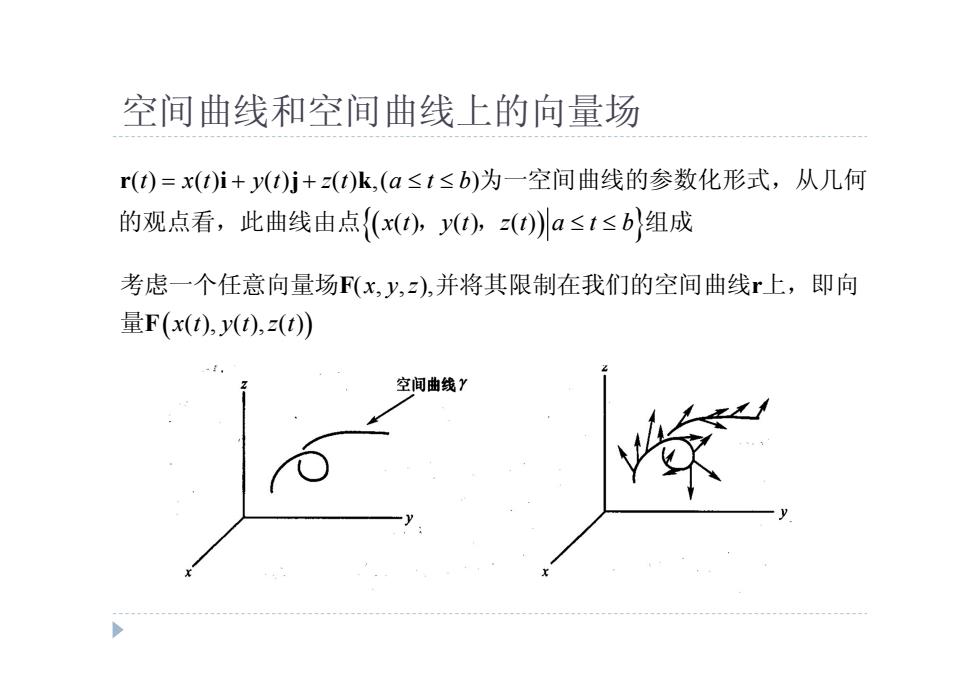
空间曲线和空间曲线上的向量场 ( ) ( ) ( ) ( ) ,( ) ( ) ( ) ( ) t x t y t z t a t b x t y t z t a t b r i j k 为一空间曲线的参数化形式,从几何 的观点看,此曲线由点 , , 组成 ( , , ), ( ), ( ), ( ) x y z x t y t z t F r F 考虑一个任意向量场 并将其限制在我们的空间曲线 上,即向 量
曲线的参数方程、参数曲线的切向量和切线 r(t)=x(t)i+y(t)j+z(t)k 切向量:r'(t)=lim r(t+△t)-r(t) △1-0 △t 切线方程:X()=r(t)+ur'(t) r'(t) t r(t+△t)
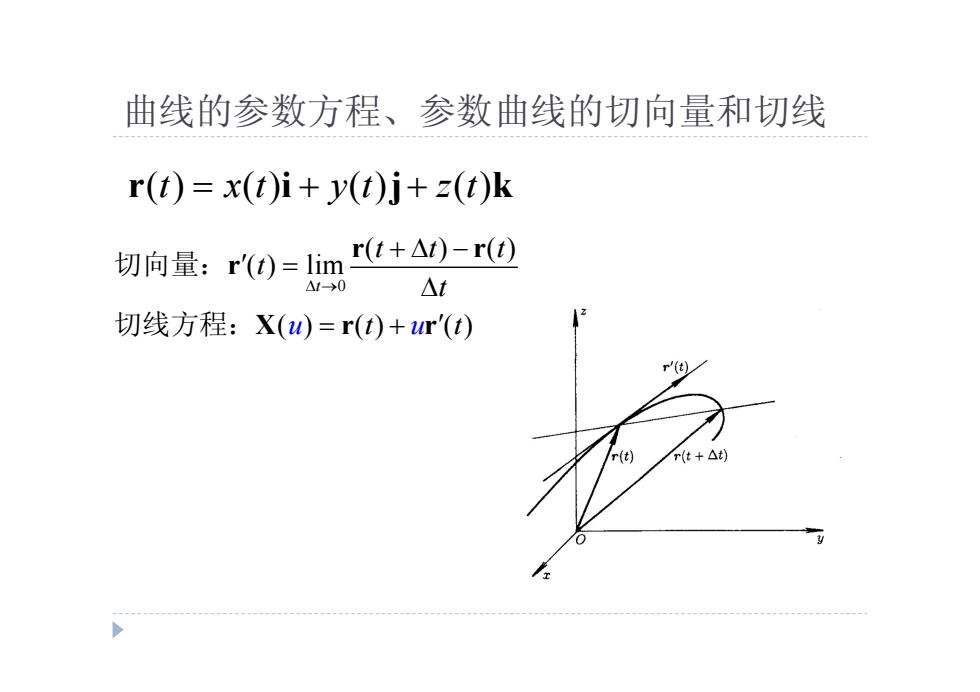
曲线的参数方程、参数曲线的切向量和切线 r i j k ( ) ( ) ( ) ( ) t x t y t z t 0 ( ) ( ) ( ) lim ( ) ( ) ( ) t u u t t t t t t t r r r X r r 切向量: 切线方程:
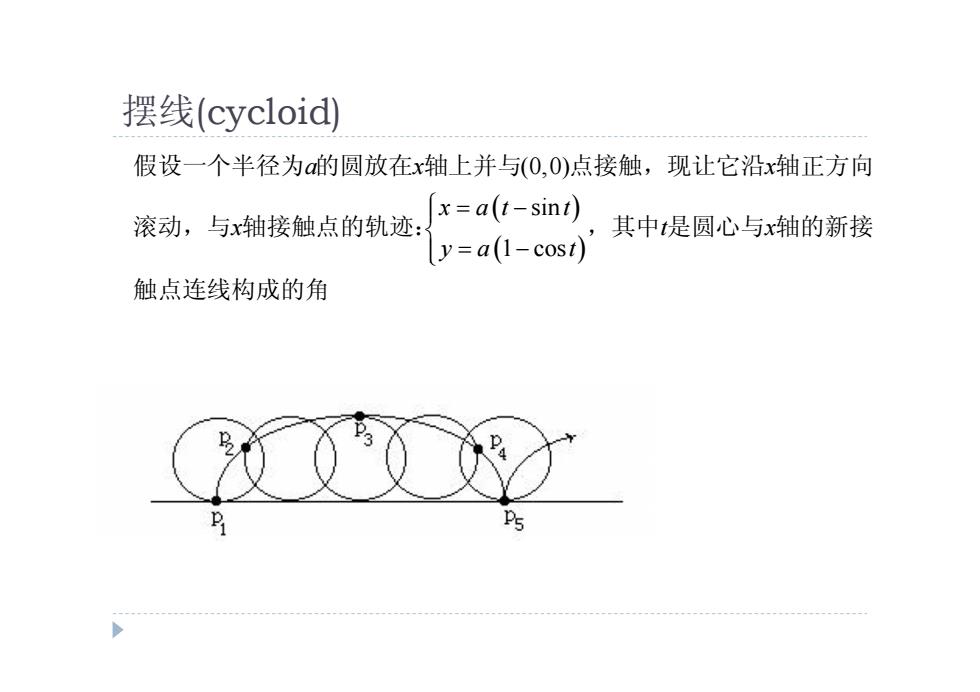
摆线(cycloid) 假设一个半径为的圆放在x轴上并与(0,0)点接触,现让它沿x轴正方向 x=a(t-sint) 滚动,与x轴接触点的轨迹: 其中是圆心与x轴的新接 y=a(1-cost) 触点连线构成的角
(0,0) sin 1 cos a x x x a t t x t x y a t 假设一个半径为 的圆放在 轴上并与 点接触,现让它沿 轴正方向 滚动,与 轴接触点的轨迹: ,其中 是圆心与 轴的新接 触点连线构成的角 摆线(cycloid)