
注:一阶线性非齐次方程初值问题的解 dy +p(x)y=g(x) dx y(xo)=yo y=yenat+goenods
注:一阶线性非齐次方程初值问题的解 0 0 ( ) ( ) 0 0 0 ( ) ( ) ) ) ( ( x x x s p t dt x p t dt x dy p x y q x dx y y x y y e q s e ds

例 求解常微分方程:少=f(x+) dx 构造变换u=x+y,上述方程变形为 d-1+f0
例 ( ) dy f x y dx 求解常微分方程: , 1 ( ) du f u d u y x x 构造变换 上述方程变形为
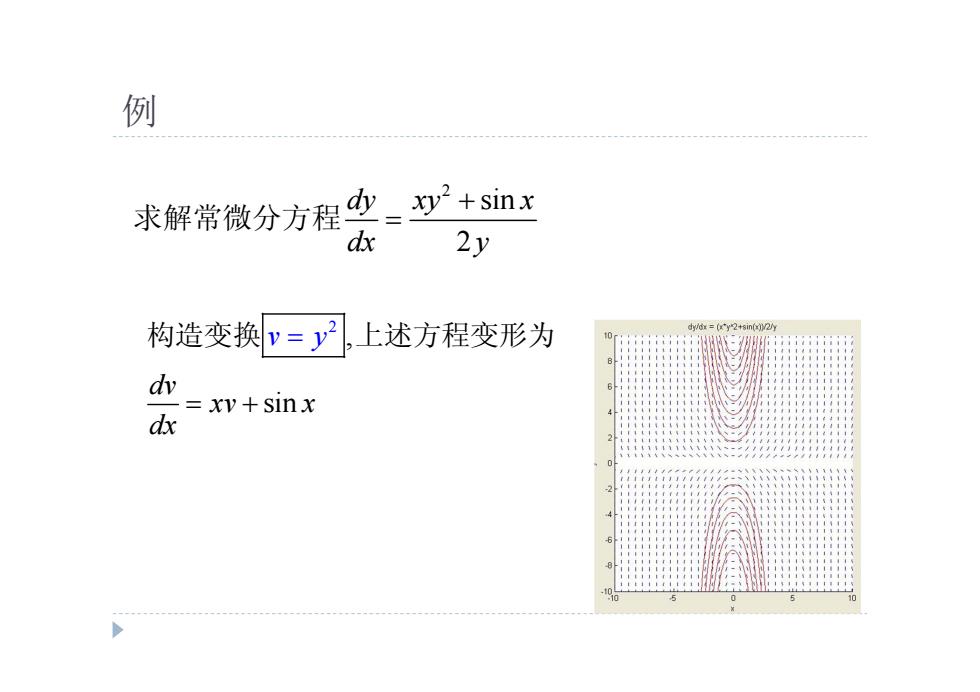
例 求解常微分方程少=y+sinx dx 2y 构造变换v=y,上述方程变形为 dv =xv+sinx dx
例 2 sin 2 dy xy x dx y 求解常微分方程 2 , sin dv xv v x dx y 构造变换 上述方程变形为
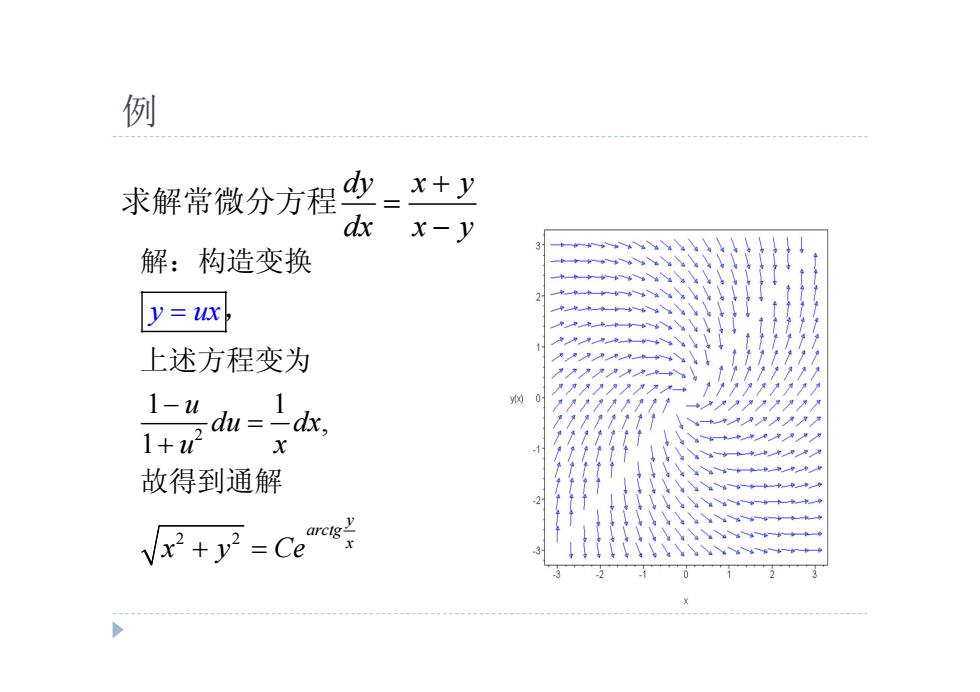
例 求解常微分方程 少_ x+y d x-y 解:构造变换 y=ux 上述方程变为 1-"d=1ak, 1+u2 故得到通解 vx2+y2=Ce
例 dy x y dx x y 求解常微分方程 2 2 2 1 1 , 1 y arctg x u du dx u x x y y Ce ux 解:构造变换 , 上述方程变为 故得到通解

例 求解常微分方程: =y+ (Bernoulli) dx y 方程两边乘以x,并构造变换u=y,方程变形为 d=2u+2x2 u=Ce2x-x2-x-
例 2 (Bernoulli) dy x y dx y 求解常微分方程: 2 2 2 2 , , 2 2 1 2 x x du u x dx u Ce x u y x 方程两边乘以 并构造变换 方程变形为