北京化工大学：《微积分》课程授课教案（专题讲稿）工科数学分析专题——曲线积分曲面积分

梯度向量场的判别 单连通区域上v=P(x,y,z)i+Q(x,y,2j+R(x,y,z)k是梯度向量场 k → 0 =0 Ox ay 0z P Q R 证明： （充分性)构造函数 x,y)=P(x2k+旷0xy+∫ R(xo2 Yo2)d 验证知v= 水 j+

梯度向量场的判别 ( , , ) ( , , ) ( , , ) 0 P x y z Q x y z R x y z x y z P Q R            v i j k i j k 单连通区域上 是梯度向量场 0 0 0 0 0 0 ( , , ) ( , , ) ( , , ) ( , , ) x y z x y z x y z P x y z dx Q x y z dy R x y z d x y z   z               v i j k 证明：（充分性）构造函数 ， 验证知

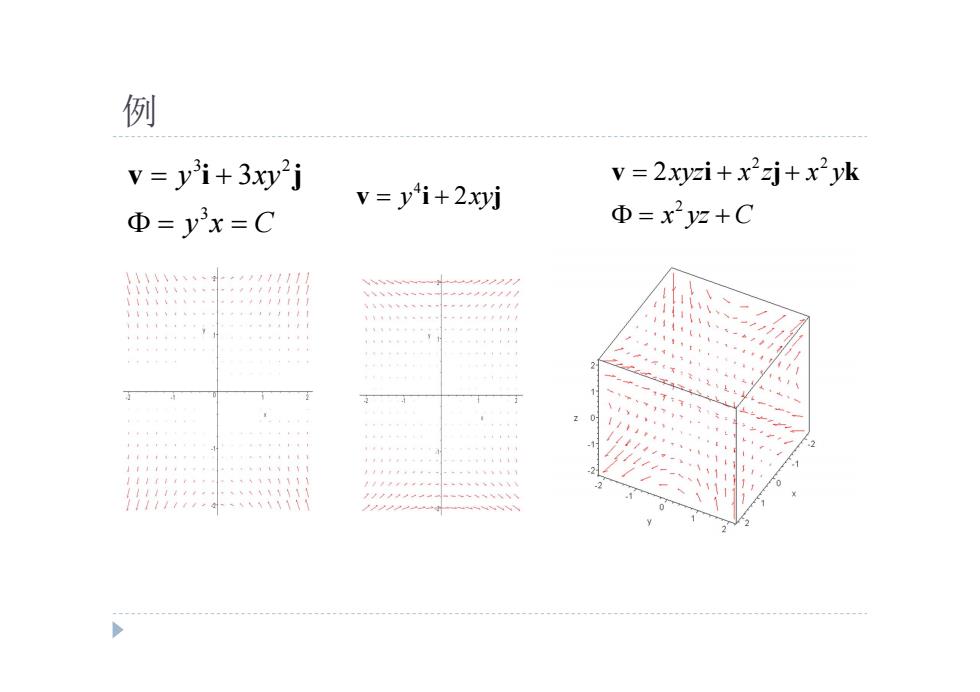
例 v=yi+3xy"j v=2xyzi+x2zj+x2yk v=yi+2xyj Φ=y3x=C Φ=x2yz+C -→→一 年年产产 人大→

例 3 2 3 y xy 3 y x C      v i j 4 v i j   y xy 2 2 2 2 2xyz x z x y x yz C       v i j k

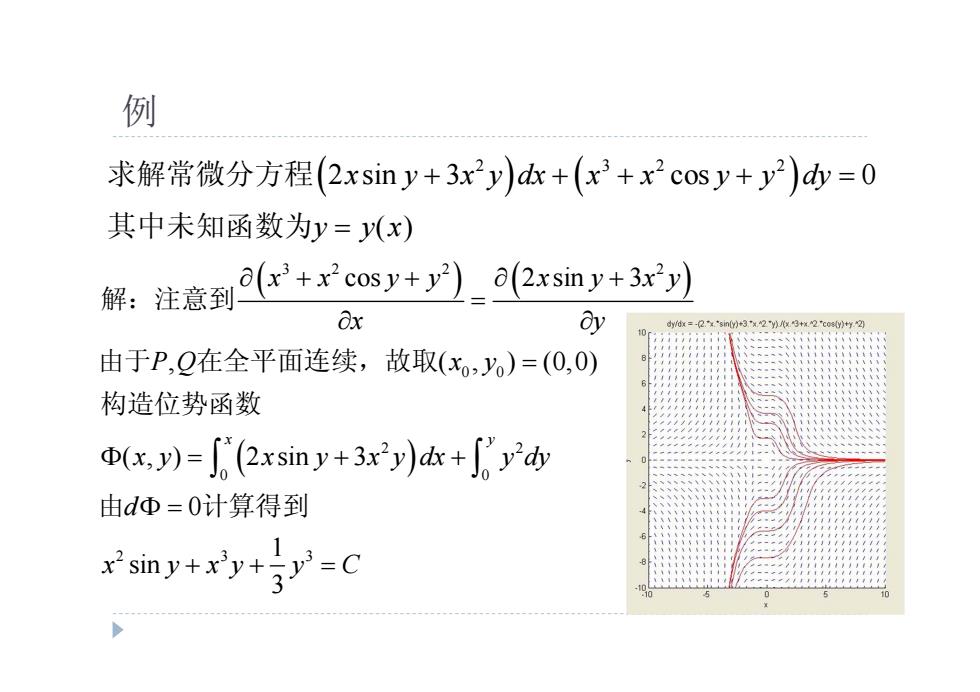
例 求解常微分方程(2 xsiny+3x2y)c+(x3+x2cosy+y2)=0 其中未知函数为y=y(x) 解：注意到'+coy+y）_a2xsny+3x) Ox 8y 2 由于P,Q在全平面连续，故取(x,)=(0,0) 构造位势函数 Φ(x,y)=(2 xsin y+3xy)c+6y少 由dΦ=0计算得到 y+xy+=C

例     2 3 2 2 2 sin 3 cos 0 ( ) x y x y dx x x y y dy y y x       求解常微分方程 其中未知函数为       3 2 2 2 0 0 2 2 0 0 2 3 3 cos 2 sin 3 , ( , ) (0,0) ( , ) 2 sin 3 0 1 sin 3 x y x x y y x y x y x y P Q x y x y x y x y dx y dy d x y x y y C                     解：注意到 由于 在全平面连续，故取 构造位势函数 由 计算得到

例 求解常微分方程：(x2+1)(y2-1)c+灯=0 其中未知量y=y(x) 两边除以(y2-)x得到 +l本+y=0,两边积分 2-19 为=1+c 其中C为任意常数 以及特解x=0

例    2 2 1 1 0 ( ) x y dx xydy y y x      求解常微分方程： 其中未知量   2 2 2 2 2 2 1 0 1 1 0 1 , x y x x y dx d e y C x x y x y C          两边除以 ，得到 ，两边积分 通解为： 其中 为任意常数 以及特解

例 求解常微分方程： +上=x,(x≠0)，未知函数y=(x) dx x 解：两边乘(=e上=H,(x≠0) y=5+(*0)

例   3 0 ( ) dy y x x y y x dx x 求解常微分方程：     ， ，未知函数     1 4 ( ) , 0 1 , 0 5 dx x x e x x C y x x x         解：两边乘