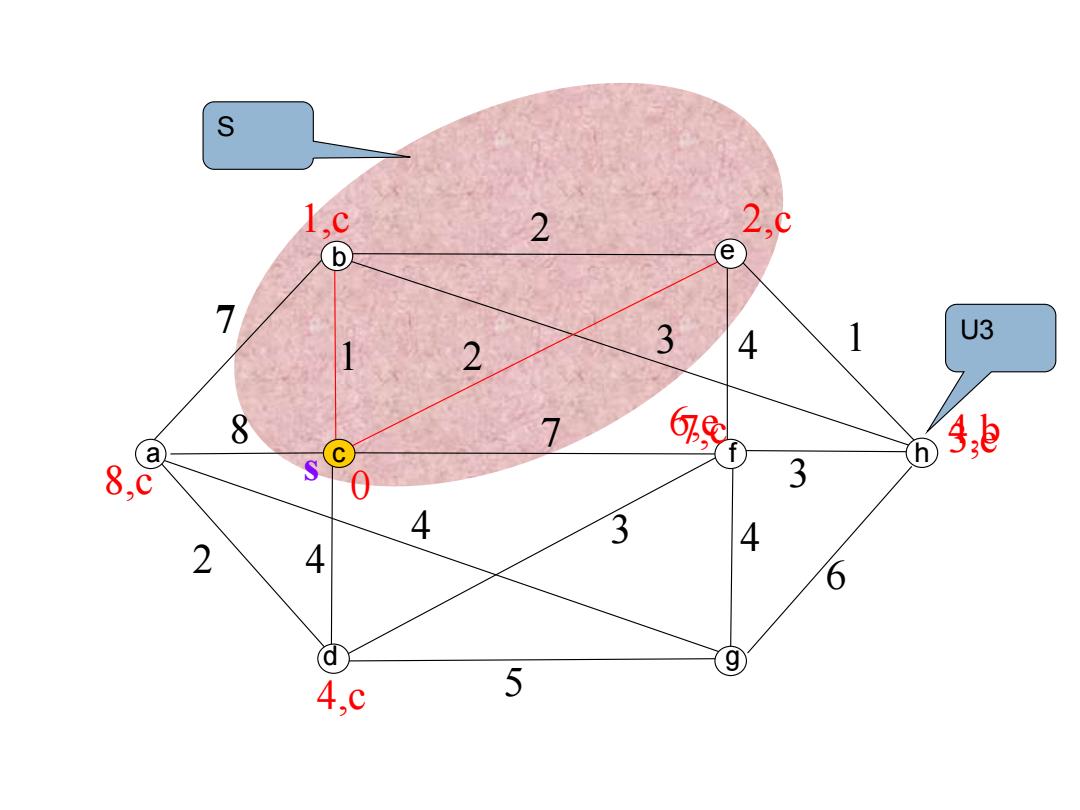
S 2 2,C b e 7 3 4 1 U3 1 2 8 5,e 8,c 3 4 3 4 2 4 6 9 4,C 5
s 7 7 2 1 2 4 1 2 4 4 8 3 5 3 4 6 3 0 1,c 2,c 8,c 7,c 4,c U3 b a cd efg h 4,b S 3,e 6,e
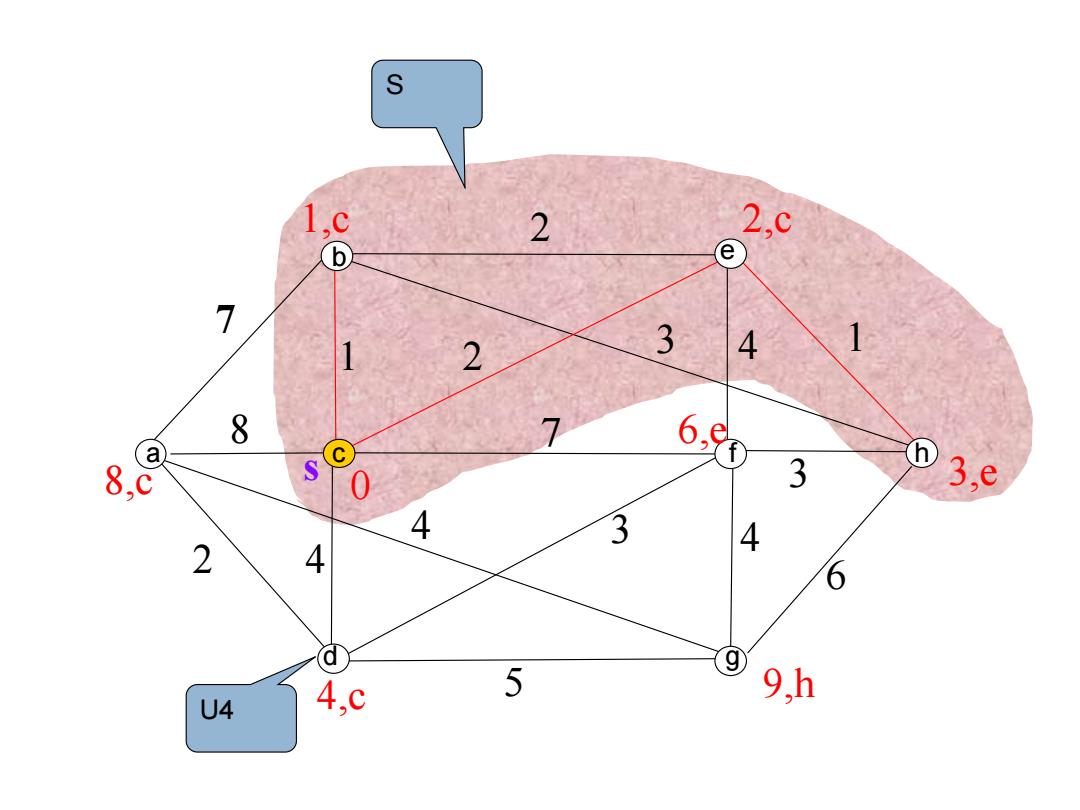
S 1 2 2,c 6 e 7 1 2 3 4 1 8 el 8,c S 3 3,e 4 3 4 2 4 6 AC 5 ⑨ 9,h U4
s 7 7 2 1 2 4 1 2 4 4 8 3 5 3 4 6 3 0 1,c 2,c 8,c 6,e 4,cb a cd efg h U4 3,e 9,h S
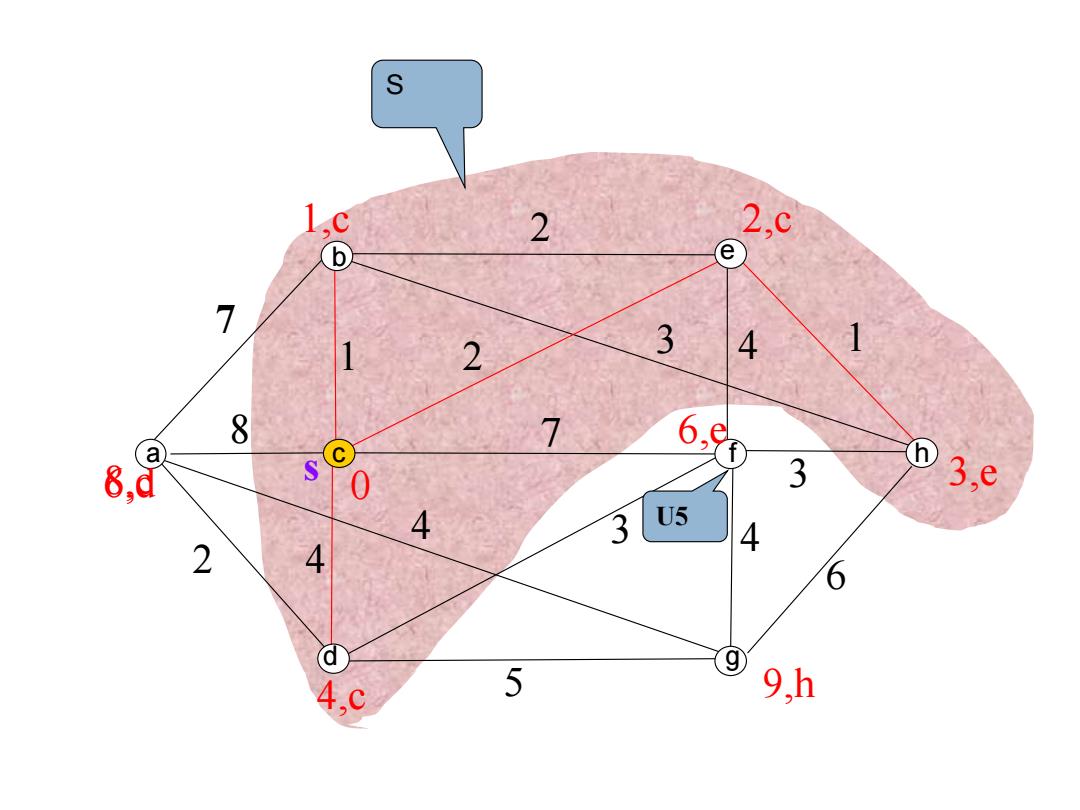
S 2 2,c b e 7 1 2 3 4 1 8 6,e 8,d ) 3 3,e 4 3 U5 4 2 4 6 9 49 5 9,h
s 7 7 2 1 2 4 1 2 4 4 8 3 5 3 4 6 3 0 1,c 2,c 8,c 6,e 4,cb a cd efg h U5 3,e 9,h S 6,d

2 2 1 3 5 8 7 6 6 0 3 4 3 2 2 2 以 3 4 5 8 b 0 2 4 4 1 2 2 5 9 7 4 2 5 3 8 7 6 3 6 0 3 4 3 2 4 4 6 5 9
s 7 7 2 1 2 3 1 2 4 4 8 3 5 3 4 6 5 01 2 6 6 4 3 9 s 7 7 2 1 2 3 1 2 4 4 8 3 5 3 4 6 5 01 2 6 6 3 9 s 7 7 2 1 2 5 1 2 4 4 8 3 5 3 4 6 3 0 1 2 6 4 9 6

Dijkstra算法的分析 口可终止性 口计数控制 ▣正确性 需证明当算法终止时 ▣L()=d(S,)对一切y成立。 口由标记中的诸确定的路径是一条最短路径 (这里s,)是s到v的最短路径长度,即距离。) 口复杂性 口O():每次迭代可能需要更新所有点(S?中的点) oO(E]Ig V):通过binaty heap
可终止性 计数控制 正确性 需证明当算法终止时 L(v)=d(s, v)对一切v成立。 由标记中的诸ui确定的路径是一条最短路径 (这里d(s,v)是s到v的最短路径长度,即距离。) 复杂性 O(n2 ):每次迭代可能需要更新所有点(S’中的点) O(|E| lg |V|):通过binary heap Dijkstra算法的分析