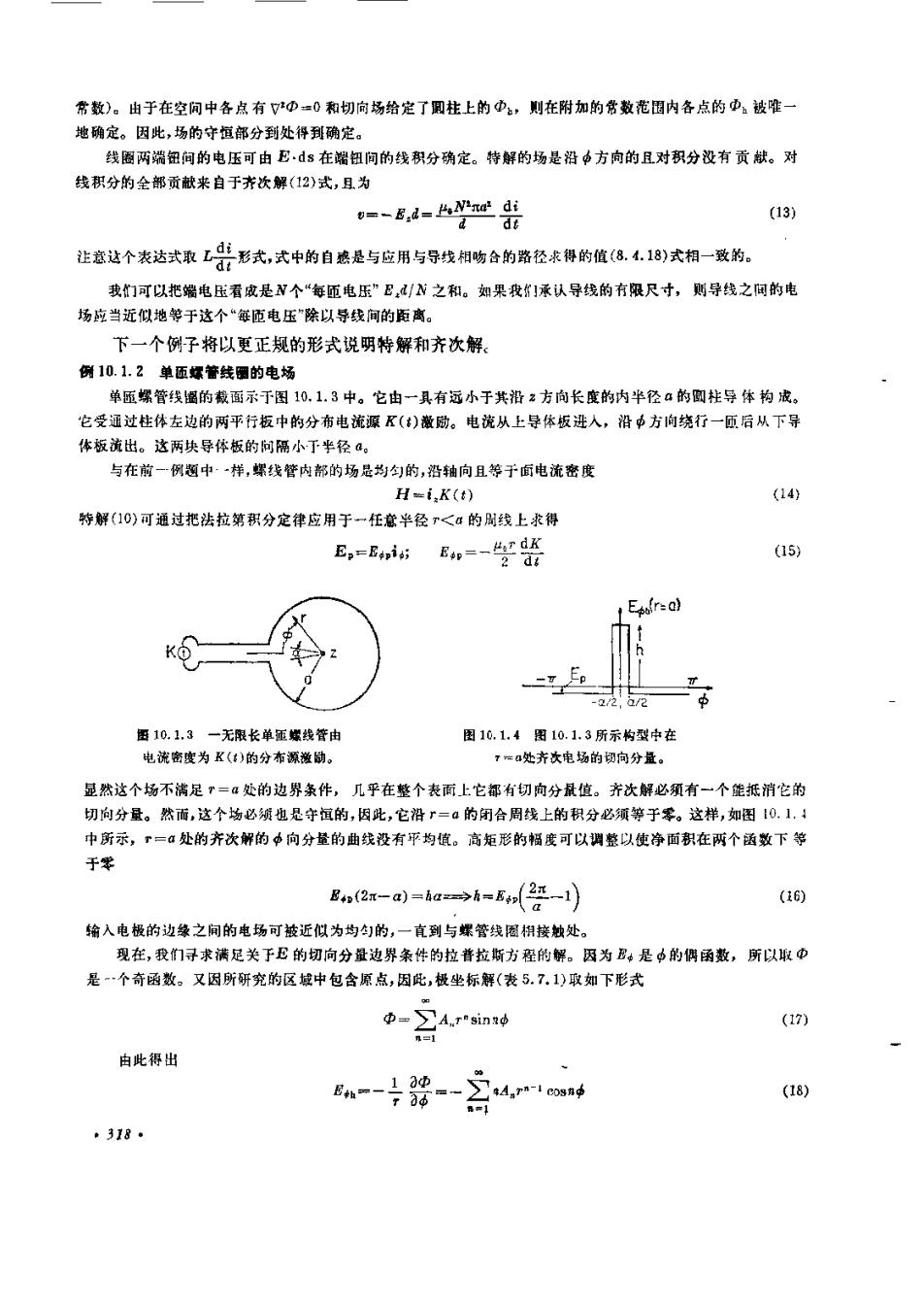
常数)。由于在空间中各点有 *Φ=0 和切向场给定了柱上的Φ,则在附加的常数范围内各点的Φ被唯地确定。因此,场的守恒部分到处得到确定。线圈两端钮间的电压可由E·ds 在端钮间的线积分确定。特解的场是沿中方向的且对积分没有贡献。对线积分的全部贡献来自于齐次解(12)式,且为--Ed-HNnd di(13)注意这个表达式取 L形式,式中的自感是与应用与导线相吻合的路径求得的值(8.4.18)式相一致的。我们可以把端电压看成是N个“每匝电压”E,a/N之和。如果我们承认导线的有限尺寸,则导线之间的电场当近似地等于这个“每匝电压除以导线间的距离下一个例子将以更正规的形式说明特解和齐次解。例10.1.2单而烁管线圜的电场单匾螺管线留的截面示于图10.1.3中。它由一其有远小于其沿2方向长度的内半径4的圆柱导体构成。它受通过柱体左边的两平行板中的分布电流源K()激励。电流从上导体板进人,沿中方向绕行一成后从下导体板流出。这两块导体板的问隔小于半径。与在前一例题中·一样,螺线管内部的场是均勾的,沿轴向且等于面电流密度H-i,K(t)(14)特解(10)可通过把法拉第积分定律应用于一柱意半径r<4 的周线上求得(15)E,=Epis;Epefr-at图10.1.3—一无限长单延螺线管由图10.1.4图10.13所示构型中在电流密度为K()的分布源激励a处齐次电场的切向分量显然这个场不满足“=α处的边男条作,几乎在整个表面上它都有切向分最值。齐次解必须有一个能抵消它的切向分量。然而,这个场必颈也是守面的,因此,它沿r=α 的闭合周线上的积分必须等于零。这样,如图 10. 1.中所示,=α 处的弃次解的本向分量的曲线没有平均值。 高矩形的幅度可以调整以使净面积在两个函数下等于*B+(2n-a) =fa>h=E+(22-1)(16)输入电极的边缘之间的电场可被近似为均勺的,一直到与螺管线圈根接触处。现在,我们寻求满足关于E的切向分量边界条件的拉普拉斯方程的解。因为B。是中的偶函数,所以取@是一个奇函数。又因所研究的区域中包含原点,因此,极坐标解(表5.7.1)取如下形式@-A.r"sins(17)由此得出E-→4,- on(18)+ 318

像在5.5节中一样,上式两边来以0m非从中元积分到中一元,即可计算出系数4.Enrtvedp+Jt E.(f-1)oosmpds(19)-Boptos mpdp=-mAma-1 因此,用于计算(17)式电位所需的系数是4Bop(r=a)sinma(20)最后,所求的电场强度是特解(15)式,与齐次解(17)式的梯度之和。sinusndiO4UR(21)innot图10.1,5中用图形表示这个解中描述的各个场的叠加情况。一个守恒场被加于-有旋场。前者在T=α处有一个是输入电极间的中的线性增长函数的电位,它从6-5/2处的下电极的负值线性地赔加在中向平面处通过零值,在/2处的上电极达一个相等的正值。随者中的继续增加,电位从这个最大值以线性方式减小,在中=180°处再次通过等,当返回到下电极时,恢复到原来的负值。因此等位线可把螺管边缘上的点与输人电极间相同电位的点连接起来。注意与这个位相关的电场的确拥有所需抵消来自有旋电场切线分量的相应图10.1.5图10.1.3所示构型中对电场变分量,其证明见上面曲线的最后一部分。度解的图形表示。通常矢量位可以方便地提供一个特解。如果用V×A 代替B,则vx(E+验)=0(22)假设A已经确定,那末上式括号中的量必须等于位Φ的梯度使A-v0E-—(23)在所研究的例题中,这个表达式的第一项就是特解,而第二项则是齐次解。10.2有限电导率导体系统中感应场的特性如果导体位于一时变磁场中,感应的电场会产生电流。从8.4节中,我们已经证明了这些电流将阻止磁场透入完纯导体。α为多大时才可以把导体看作是完纯的呢:在下面两节中,我们应用特定的解析模型来回答这个问题。现在我们从用来确定有限电导率导体中电流的分布、持续时间和量值的法拉第、安培和欧姆定律之间的相互影响的讨论来作为开端。应用于图10.2.1中所示的回路C,和表面8上的法拉第定律的积分形式是.319

f E-ds=--j. Bda(1)把欧姆定律J=αE代人(1)式,使沿回路C.的管子中环行的电流密度与被包围的磁通联系起来,有图10.2.1按照法拉第定单所感应的电流沿剧线C二-ds=-%[, Bda(2)环行。通过安培定律,它产生沿履线C的磁场这个表达式适用于导体中的每,一个环行的电流“软管”。让我们把注意力集中于这样一个软管上。电流平行于软管流动,因此,J.ds=Jds。假设这个软管的截面积是 A(s),则 JA(s)=i,i是软管中的总电流,且40)ds=R(3)是软管的电阻。因此iR--(4) 方程(2)描写了时变磁通怎样引起环行电流。而安培定律陈述了电流怎样依次又产生磁场。 H.ds-f. J.da(5)典型地说,场沿图10.2.1中所示回路C,闭合,它是被J穿过的。对于B的高斯定律,安培定律提供了J与它所产生的H的关系。这个信息可用“集总电路”关系来概括成a-I.(6)(4)和(6)两式相结合可提供对电路中电流i((t)的一个微分方程,这个微分方程的等效电路是图10.2.1所示的一个电阻器R和电感器L的串联电路。它的解是时间常数为L/B的随时间作指数衰减的函数(2)和(5)两式即法拉第定律、安培和欧姆定律相结合可确定】和H。这个场的问题对应干“电路”的连续集。我们将发现场对时间的依从关系受具有 R/Z性质的时间常数所支配。这个时间常数将有如下形式菜十五Tm=μGlil2(7)与EQS的电荷弛像时间相反,这个磁扩散时间依赖于这里用1,和12表示的两个特征长度的乘积。对于给定的时间变率和电导率,系统越大,其特性越类似完纯导体。21虽然我们将不再应用积分定律来确定下一节中有限电导率导体系统中的场,但它们还常常被用于作工程近似。下面的演示应用粗略近似定量化来作为通常如何应用场的理论来解决实际问题的典型方式。演示 10. 2. 埃杰顿低音扬适器图10.2.2中C=25uF的电容器起初被充电列=4kV。。然后接解时放电开关,使电容器能够·320
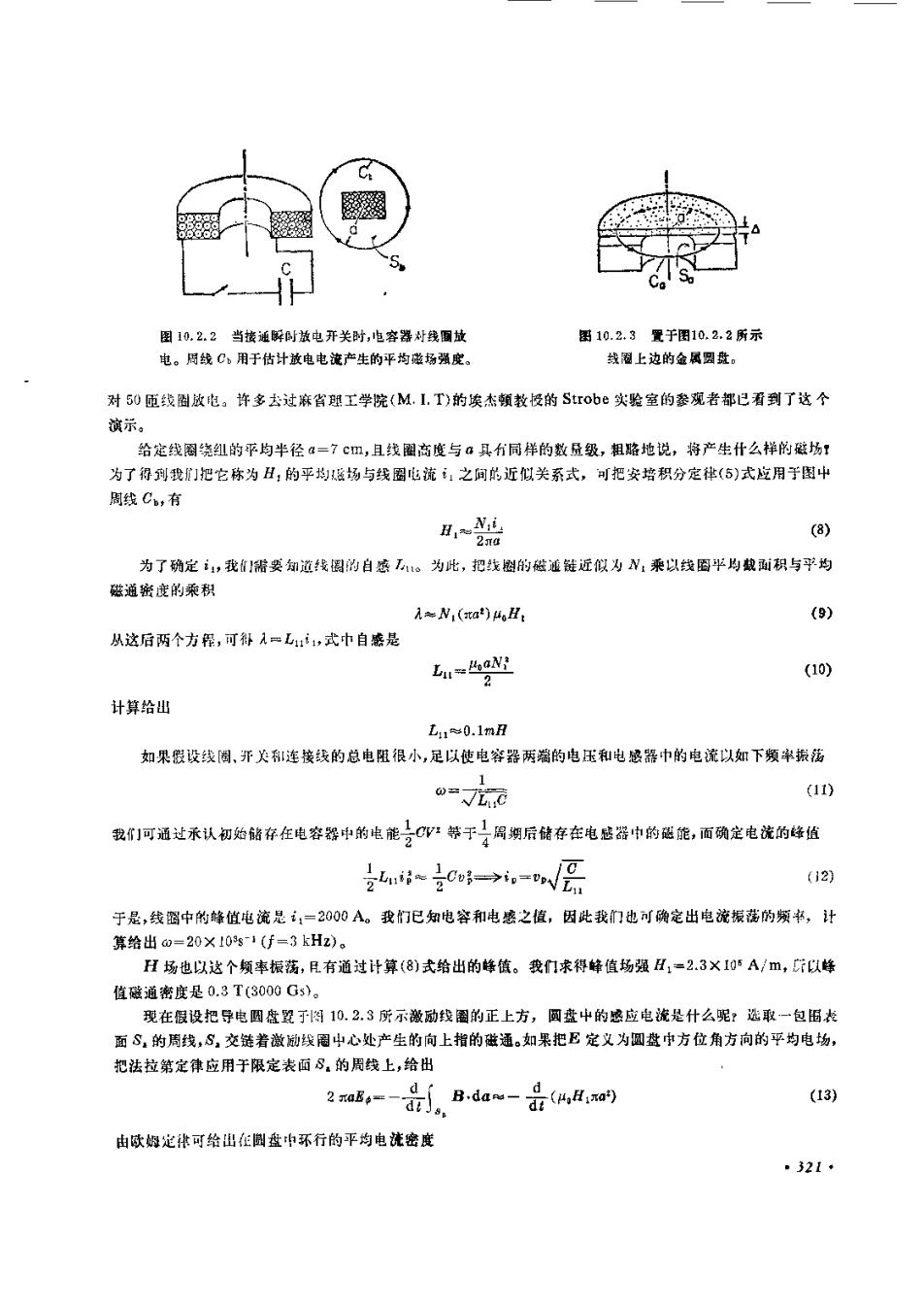
图10.2.2当接通瞬时放电开关时,电容器对线圖图10.2.8置于图10.2.2所示电。周线C、用于估计放电电流产生的平均磁场强度。线圈上边的金属园盘。对50匝线圈放电,许多去过麻省班工学院(M.I.T)的埃杰颤教授的Strobe实验室的奏观者都已看到了这演示cm,且线圈商度与α其有同样的数显级,粗地说,将产生什么样的磁场合定线图绕纽的平均半径为了得到我们把它称为H,的平均儿滋场与线圈电流,之间能近似关系式,可把安培积分定律(5)式应用于图中周线C,有i~?为了确定让,我们需要知道线摄的自感Lo为此,把线料的磁通链近似为N,乘以线圖平均数面积与平均磁通密度的乘积(9)AN(ra)H)从这后两个方程,可得入L,式中自感是LuagN.(10)计算给出Ln~0.1mH如果假设线圖、开关和连接线的总电阻很小,足以使电容器两端的电压和电感器中的电流以如下频率振荡(nO=VLIC我们可通过承认初始储存在电容器中的电能CV等于于周期后储存在电感器中的磁能,面确定电流的峰值1u=E(12)于是,线圈中的峰值电流是1,=2000A。我们已知电容和电感之值,因此我门也可确定出电流振诺的频书,计算给出 0=20×10%g-1(f=3kHz)。H场也以这个频率振荡,且有道过计算(8)式给出的峰值。我们求得峰值场强H,=2.3×10 A/m,斤以蜂值磁通密度是0.3 T(3000 Gs)现在假设把导电圆盘暨于图10.2.3所示激励线圈的正上方,圆盘中的感应电流是什么呢?选取一包围表面S,的周线,S,交链着激励线圈中心处产生的向上指的磁通。如果把E定义为圆盘中方位角方向的平均电场,把法拉第定律应用于限定表面8,的周线上,给出2 waB,--j. Bda-(μ)(13)由欧姆定律可给出在圆盘中环行的平均电滤密度.321

J,=aE,=H"dH(14)如果行人用他的于去代替这个圆裁,他将感觉列多大的电流密度呢?为了确死婚俏电流,用のl,代替导数。对于人手来说,gα1S/m,可由(14)式给出电流缩度为20mA/cm。这已超过对人身提供一次"电击的值铝盘的电导率是非带大的,约为3.5×10 S/m。根据<14)式,其中的电流密度应比人手中的电流案度大3500方倍。然而应注意在应用安培定律来确定激励场时,我们已经忽略了同盘中感应电淡的责献。安培积分定律也能应用于近似分析圆愈中电流所感应的磁场。把安培定律应用于与阅盘中环流相交链的周线:面不是与激励线圈电流相交链的回路1,则(2)式要求Hu~(15)这里,感应电流在其中环行的阅殖的截面积可近似为圆就厚度1和乎均半径α的乘积。由(14)和(15)式可导得感应场亏外随场在相同的数量级,如与r(16)式中(17)三uoA往意m取式(7)的形式,共中l=△和1,=。一个原度A=2mm,4=7cm,tm=6ms的铝盘来说,0t.,4~10,与感应电流相关的磁场是可以与激励线圈施加的磁场相比较的。圆盘表面因此是个其上各点n·B~0的表面。当它们沿径向向外转时,尚上穿过激励线图中心的磁通密度线被收集在激励线圈和铝盘之间。这些磁通密度线画于图 10. 2.4中。用例 9.7. 4 中引人的术语来说,国盘就是变压器的次级尧组。事上,ta是次级绕组的时间常数 Las/ R.其中 R,和 La。是措述圆盘的电路的电阻和电感。实际上,作为理想变压器运行的条件(9. 7.26)式相觉于有关系@T㎡/4元》1。电力变压器中的绕组受到我们现在演示的这些力的作用fitJXE 图10.2.4感成在金属盘中的电流焰于产生一个附图10.2.5因为作用在盘上的磁力总是正的,且止由激励线圈所施加的磁场。这些电流导致一个力作延续叶间T比把盘拉离线图邻近所需的时间用于圆盘上。此力趋于将金属盘推向上方。短,因此可把它用·录值为了T的冲激求摘n如果将“个铝盘置于线图上片闭合开关,将会出现一系列应用。首先,将在一·冲击,正确绝启示可把圆盘用作声学传感器。深海声音测深即是其典型应用。由洛仑兹定律(见11.9书)可给出产生此声音的力密度F(N/msF=JXμ.H(18)注意无论激励电流的极性如何,也即无论平均磁场的方向如何,此力密度总是向上作用的。它是一个准床力。如果将盘中的电流分布用面电流密度K描述,并把B取作它的平均值的半(例11.9.3中将解释因子1/2),则作用在这个盘上的向上的总力是①正如我们将在下节中肴到的,因为计算不是自洽的,不等式 T》1表明感度场可以与外施场相比较,但不能超过外施场。· 322