
三 曲线族的绘制 ·【例5-1-3】三次曲线的方程为, y=ax3 +cx 。1 试探讨时参数a和c对其图形的影响.图5-1-3c 和a取不同值时y=ax3+cx的曲线族 ·解:◆方法因为函数比较简单,可以直接写 入绘图语句中,用循环语句来改变参数.注意 坐标的设定方法,以得到适于观察的图形。 给出的程序不是唯一的,例如也可用fplot函 数等
三 曲线族的绘制 • 【例5-1-3】 三次曲线的方程为, • 试探讨参数a和c对其图形的影响.图5-1-3 c 和a取不同值时y=ax3+cx的曲线族 • 解:◆方法 因为函数比较简单,可以直接写 入绘图语句中,用循环语句来改变参数.注意 坐标的设定方法,以得到适于观察的图形。 给出的程序不是唯一的,例如也可用fplot函 数等, 3 y ax cx

画曲线族的程序 ·X=-2:0.1:2; %给定x数组, ·subplot(1,2,1) %分两个画面绘图 。forc=-3:3 plot(x,x.^3+c*x),hold on, %a=1,取不同的c ·end,grid on ·axis('equal'),axis(-22-33]),%x,y坐标等比例 ·subplot(1,2,2), ·fora=-3:3plot(x,a*x.3+x), %c=1,取不同的a ·hold on,end,grid on axis(equal'),axis([-2 2-3 3])
画曲线族的程序 • x=-2:0.1:2; % 给定x数组, • subplot(1,2,1) % 分两个画面绘图 • for c=-3:3 • plot(x,x.^3+c*x), hold on, % a=1,取不同的c • end, grid on • axis('equal'), axis([-2 2 -3 3]), % x,y坐标等比例 • subplot(1,2,2), • for a=-3:3 plot(x,a*x.^3+x), % c=1,取不同的a • hold on, end , grid on • axis('equal'), axis([-2 2 -3 3])
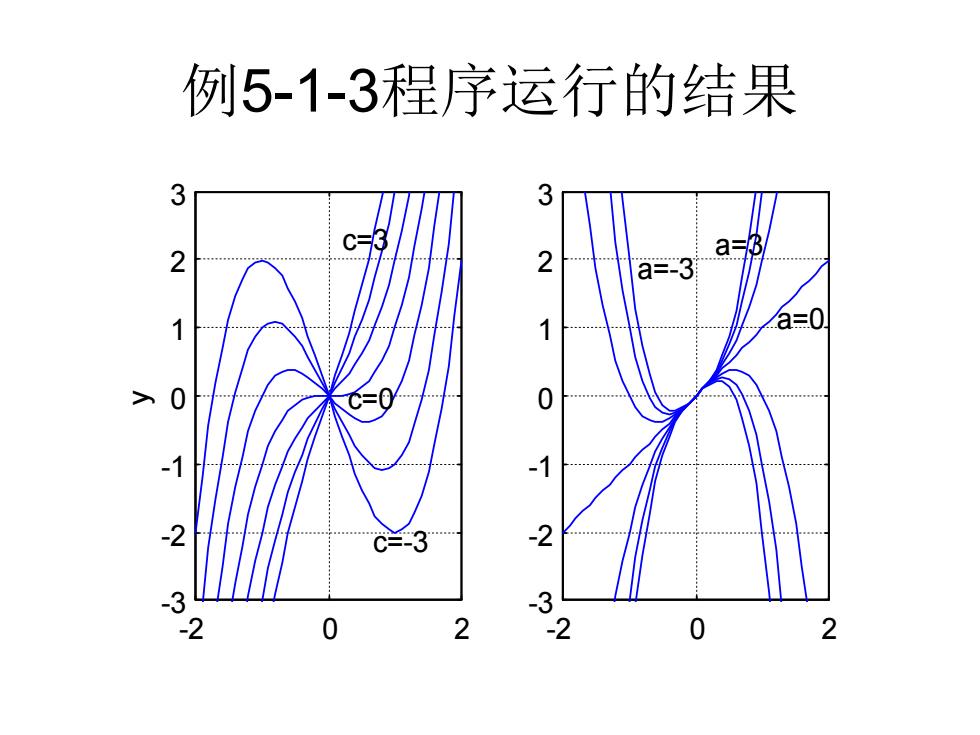
例5-1-3程序运行的结果 2 a=8 a=3 a三0 3 3 -2 0 2 -2 0 2
例5-1-3程序运行的结果 -2 0 2 -3 -2 -1 0 1 2 3 x y c=0 c=-3 c=3 -2 0 2 -3 -2 -1 0 1 2 3 a=-3 a=3 a=0

四.极限判别 【例5-1-4】极限的定义和判别 用MATLAB来表达推理过程是比较困难的,因为它必 须与实际的数值联系起来。比如无法用无穷小和高阶无穷 小的概念,只能用e-10,e-20等数值。不过极限的定义恰 恰用了δ和ε这些数的概念,因此不难用程序表达。 。 解:◆建模用函数极限的定义 对于函数y=(x),当任意给定一个正数ε时,有一个对应 的正数δ存在,使得当0<x。-x<6时, A-f(x)<8 ·其中为绝对值符号,则A就是f)在时的极限,如果找不到 这样的δ,A就不是它的极限
四.极限判别 • 【例5-1-4】 极限的定义和判别 • 用MATLAB来表达推理过程是比较困难的,因为它必 须与实际的数值联系起来。比如无法用无穷小和高阶无穷 小的概念,只能用e-10,e-20等数值。不过极限的定义恰 恰用了δ和ε这些数的概念,因此不难用程序表达。 • 解:◆ 建模 用函数极限的定义 • 对于函数y=f(x),当任意给定一个正数ε时,有一个对应 的正数δ存在,使得当 时, • 其中为绝对值符号,则A就是f(x)在时的极限,如果找不到 这样的δ,A就不是它的极限。 0 c x x A f (x)