
用函数程序方法 此方法,要用两个程序文件 主程序exn511b为: dt=0.01;t=[0:dt:1.5];w=4*sqrt(3); y=exn511bf(t,w);Dy=diff(y)/dt; %绘图和加标注的程序略去 另要建立一个函数文件exn511bf.m,其内容为: function xvalues=ex511bf(tvalues,w) %此函数文件,应该能用元素群运算。 xvalues=w*exp(-4*tvalues).*sin(w*tvalues pi/3);
用函数程序方法 此方法, 要用两个程序文件 主程序exn511b为: dt=0.01; t=[0:dt:1.5]; w= 4*sqrt(3); y=exn511bf(t,w); Dy=diff(y)/dt; % 绘图和加标注的程序略去 另要建立一个函数文件exn511bf.m,其内容为: function xvalues= ex511bf (tvalues,w) % 此函数文件,应该能用元素群运算。 xvalues=w*exp(-4*tvalues).*sin(w*tvalues + pi/3);

程序运行结果 ·运行这两种程序都得到图5-1-1的曲线。为了节省 篇幅,我们没让显示y的数据。以后的各例中还将 删略绘图时的标注语句。从本例看,第二种方法 似乎更麻烦一些,但它具备模块化的特点。当程 序中要反复多次调用此函数,而且输入不同自变 量时,利用函数文件可大大简化编程。我们应该 掌握这种方法。两次应用dif函数或用dif(y,2)可以 求y的二次导数。 ·改变背景色为白色的命令 set(gcf,'color','w')
程序运行结果 • 运行这两种程序都得到图5-1-1的曲线。为了节省 篇幅,我们没让显示y的数据。以后的各例中还将 删略绘图时的标注语句。从本例看,第二种方法 似乎更麻烦一些,但它具备模块化的特点。当程 序中要反复多次调用此函数,而且输入不同自变 量时,利用函数文件可大大简化编程。我们应该 掌握这种方法。两次应用diff函数或用diff(y,2)可以 求y的二次导数。 • 改变背景色为白色的命令 set(gcf, 'color' , 'w')
参变方程的计算和绘图 【例5-1-2】 摆线的绘制 ·当圆轮在平面上滚动时, 轮上任一点所画出的轨迹 称为摆线。如果这一点不 在圆周上而在圆内,则生 成内摆线; 如果该点在圆外,即离圆 心距离大于半径,则生成 外摆线
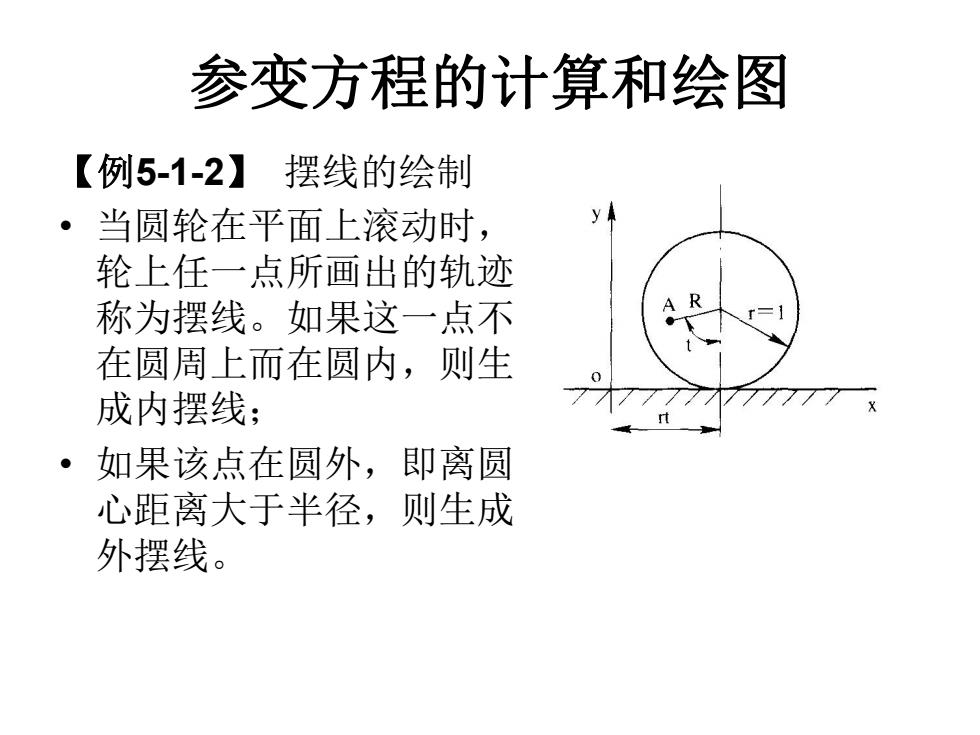
参变方程的计算和绘图 【例5-1-2】 摆线的绘制 • 当圆轮在平面上滚动时, 轮上任一点所画出的轨迹 称为摆线。如果这一点不 在圆周上而在圆内,则生 成内摆线; • 如果该点在圆外,即离圆 心距离大于半径,则生成 外摆线

摆线绘制的程序 ◆建模:其普遍方程可表为: x =rt -Rsin t y=Rcos t ◆MATLAB程序eXn512: ·t=0:0.1:10; %设定参数数组 r=input('r='),R=input('R=') %输入常数 ·x=r*t-R*sin();y=r-R*cos(t);%计算x,y ·plot(x,y),axis('equal)%绘图
摆线绘制的程序 ◆建模:其普遍方程可表为: x = rt - Rsin t y= Rcos t ◆ MATLAB程序exn512: • t=0:0.1:10; % 设定参数数组 • r=input('r='),R=input('R=') %输入常数 • x=r*t-R*sin(t); y=r-R*cos(t); % 计算x,y • plot(x,y),axis('equal') % 绘图

摆线绘制程序的结果 ·设r=1,令R=r,R=0.7 及R=1.5时得到的摆 线、内摆线和外摆线 外摆线 都绘于图5-1-3中。为 摆线 了显示摆线的正确形 内摆线 状,x,y坐标保持等比 例是很重要的,因此 程序中要加 axis(equal')语句
摆线绘制程序的结果 • 设r=1,令R=r, R=0.7 及R=1.5时得到的摆 线、内摆线和外摆线 都绘于图5-1-3中。为 了显示摆线的正确形 状,x,y坐标保持等比 例是很重要的,因此 程序中要加 axis(‘equal’)语句。 0 2 4 6 8 - 101234 摆 线 外 摆 线 内 摆 线