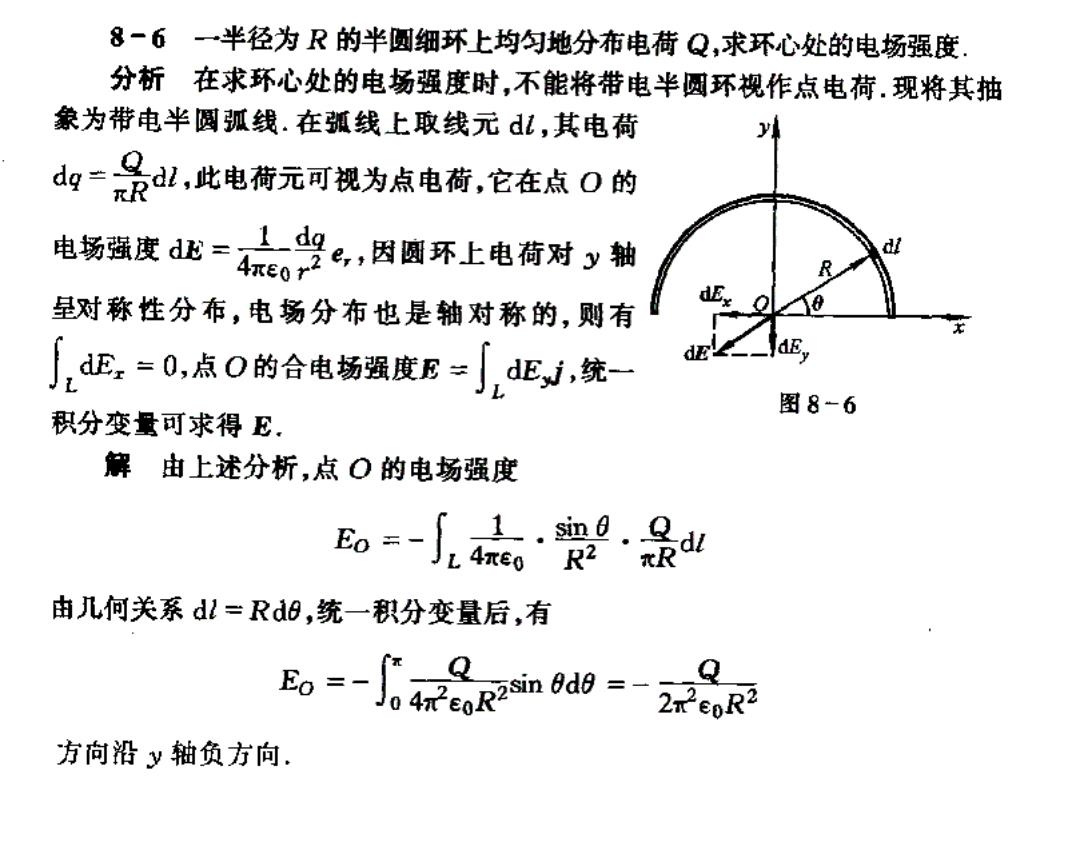
8-6 一半径为R的半圆细环上均匀地分布电荷Q,求环心处的电场强度. 分析在求环心处的电场强度时,不能将带电半圆环视作点电荷.现将其抽 象为带电半圆弧线.在弧线上取线元l,其电荷 d山一景,此电荷元可视为点电荷,它在点O的 电扬强度d止=太当。,因周环上电荷对y轴 呈对称性分布,电场分布也是轴对称的,则有 Jd证=0,点0的合电场强度E=JdE,统 积分变量可求得E. 图8-6 解由上述分析,点O的电场强度 由儿何关系dl=Rd的,统一积分变量后,有 Eo--0 4coR2in 0dg=-20R Q 方向沿y轴负方向

8一7··半径为R的半隙壳,均匀地带有电荷,电荷面密度为G,求球心处 电场强度的大小 分析这仍是一个连续带电体问题,求解的 关键在于如何取电荷元 现将半球壳分制为一组平行的细圆环(留 8一7),从教材第8一3节的例1可以看出,所有 平行圆环在轴线上P处的电场强度方向都相 同,将所有带电圆环的电场强度积分,即可求得 球心O处的电场强度. 解将半球壳分割为一组平行细圆环,任一 个圆环所带电荷元dg=adS=o2元R2sin9d8, 在点O激发的电场强度为 图8-7 rdg 4πe0(z2+-2)3 由于平行细圆环在点O激发的电场强度方向相同,利用几何关系士=Rs日, r=Rsin8统一积分变量,有 0(2强=e9, dE=1 xdg 4neoR3'o·2xR2sin0u0 osin goos edg 7e0 积分得 E- 27是sn0as0d0=460 J02e0
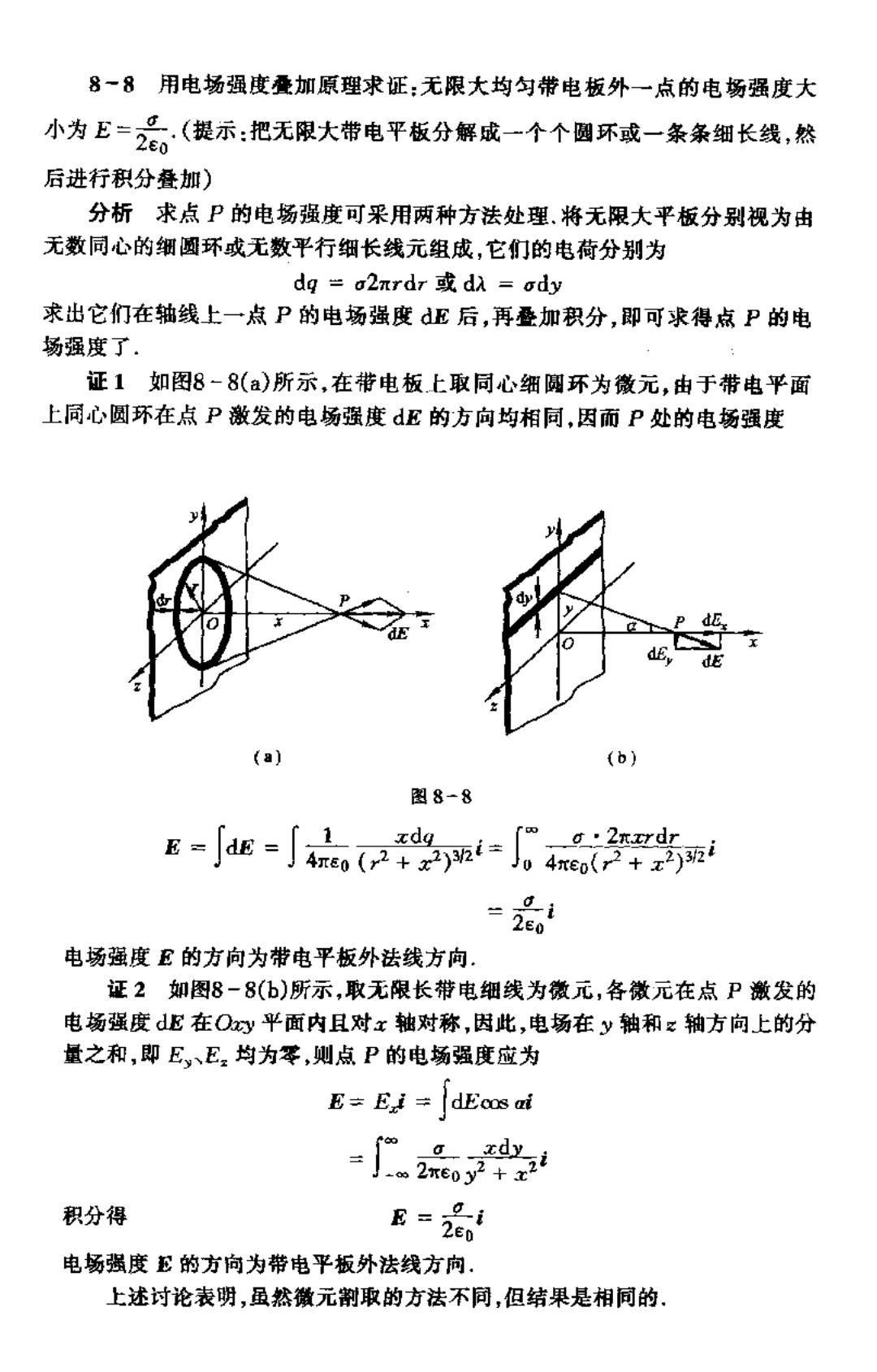
8一8用电扬强度叠加原理求证:无限大均匀带电板外一点的电畅强度大 小为E=名。(提示:把无限大带电平板分解成一个个圈环或一条条细长线,然 后进行积分叠加) 分析求点P的电场强度可采用两种方法处理.将无限大平板分别视为由 无数同心的细圆环或无数平行细长线元组成,它们的电荷分别为 dg=a2mrdr或d=ody 求出它们在轴线上一点P的电场强度dE后,再叠加积分,即可求得点P的电 场强度了. 证1如图8-8()所示,在带电板上取同心细圆环为微元,由于带电平面 上同心圆环在点P激发的电场强度dE的方向均相同,因而P处的电场强度 (a) (b) 图8-8 g-小版-学-4i舞 电场蕴度E的方向为带电平板外法线方向。 证2如图8-8(b)所示,取无限长带电细线为微元,各徽元在点P激发的 电杨强度dE在Oy平面内且对x轴对称,因此,电杨在y轴和x轴方向上的分 量之和,即E、E均为零,则点P的电场强度应为 E=Ei=dEcos ai -2品 积分得 E=品 电畅强度E的方向为带电平板外法线方向, 上述讨论表明,虽然徽元削取的方法不同,但结果是相同的
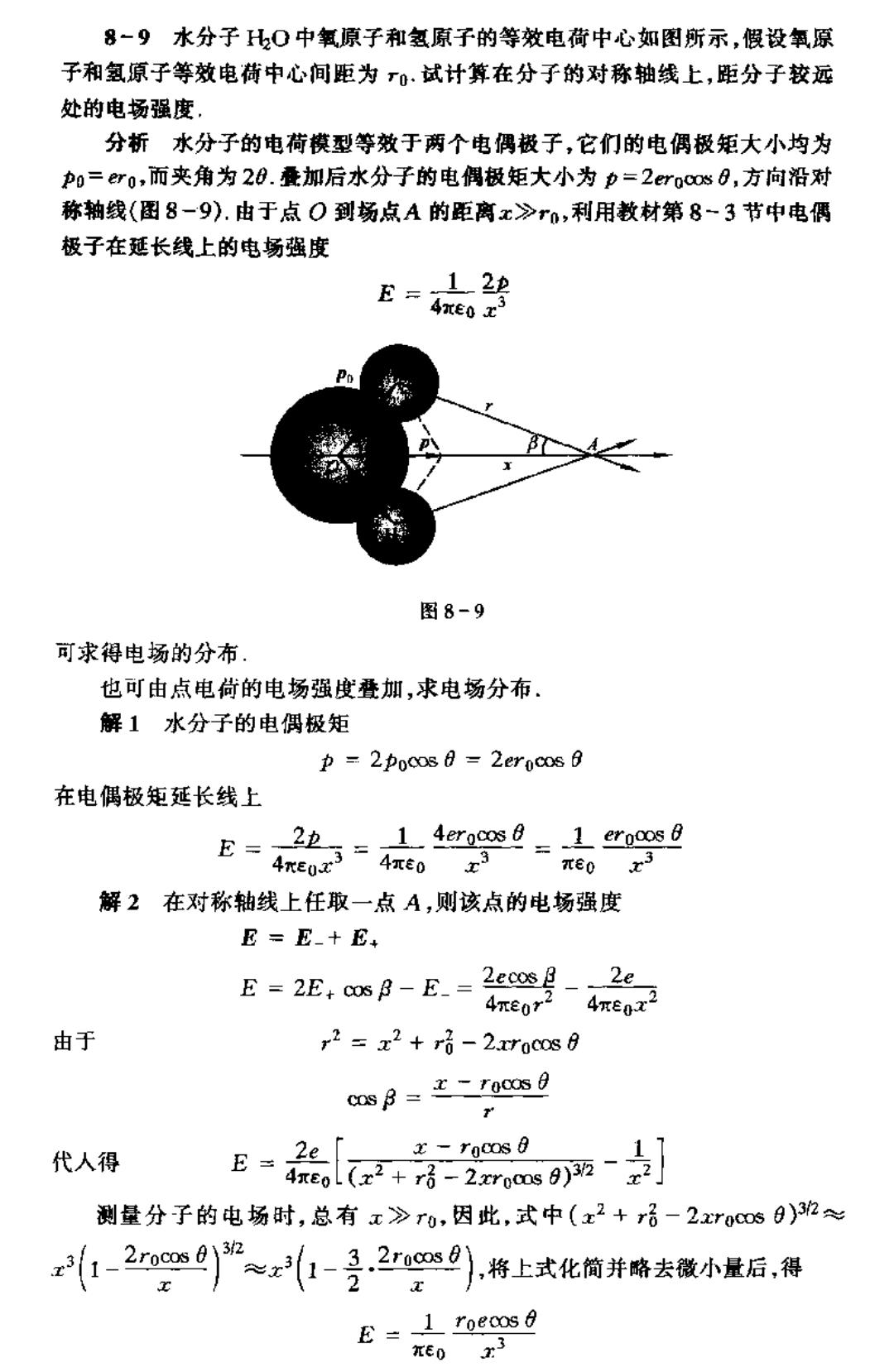
8-9水分子比0中氧原子和氢原子的等效电荷中心如图所示,假设氧原 子和氢原子等效电荷中心间距为0.试计算在分子的对称轴线上,距分子较远 处的电场强度, 分析水分子的电荷模型等效于两个电偶极子,它们的电偶极矩大小均为 0=r0,而夹角为28.囊加后水分子的电阀极矩大小为p=2rocs0,方向沿对 称轴线(图8-9).由于点O到场点A的距离x》r0,利用教材第8一3节中电偶 极子在延长线上的电场强度 .122 E=40工 图8-9 可求得电场的分布 也可由点电尚的电场强度叠加,求电场分布 解1水分子的电倒极矩 p=2Pocos d 2erocos 6 在电偶极矩延长线上 E=- 2=49=1gos旦 2 RE 4e0x3 REo x3 解2在对称轴线上任取一点A,则该点的电场强度 E=E-十E: E=2E,cos B-E.=2ccoe82e 4元e0r2 由于 r2=x2+r7-2ra0s8 COs B=roc0 0 《 代人得 lx+-2ma9] x-racos 0 测量分子的电场时,总有x》r0,因此,式中(x2+r弓-2ro050)3欢≈ -22)”1-是22)将上式化筒并略去徽小量后,得 E =1 roecos KE0

8一10两条无限长平行直导线相距为r0,均匀带有等量异号电荷,电荷线 密度为λ.(1)求两导线构成的平面上任·点的电场强度(设该点到其中一线的 垂直距离为x);(2)求每一根导线上单位长度导线受到另一根导线上电荷作用 的电场力. 分折(1)在两导线构成的平面上任一点 的电场强度为两导线单独在此所激发的电场的 叠加. (2)由F=gE,单位长度导线所受的电场 力等于另一根导线在该导线处的电场强度乘以 单位长度导线所带电的量,即:F=E.应该注 意:式中的电场强度E是除去自身电荷外其它 电荷的合电场强度,电荷自身建立的电场不会对 自身电荷产生作用力 解(1)设点P在导线构成的平面上, E+、E-分别表示正、负带电导线在P点的电场 强度,则有 图8-10 ro-x ro =2E0x(r0-x1 (2)设F,,F-分别表示正、负带电导线单位长度所受的电场力,则有 F,=迟.=20 F.=-E,=-2a70 显然有F+=一F,相互作用力大小相等,方向相反,两导线相互吸引