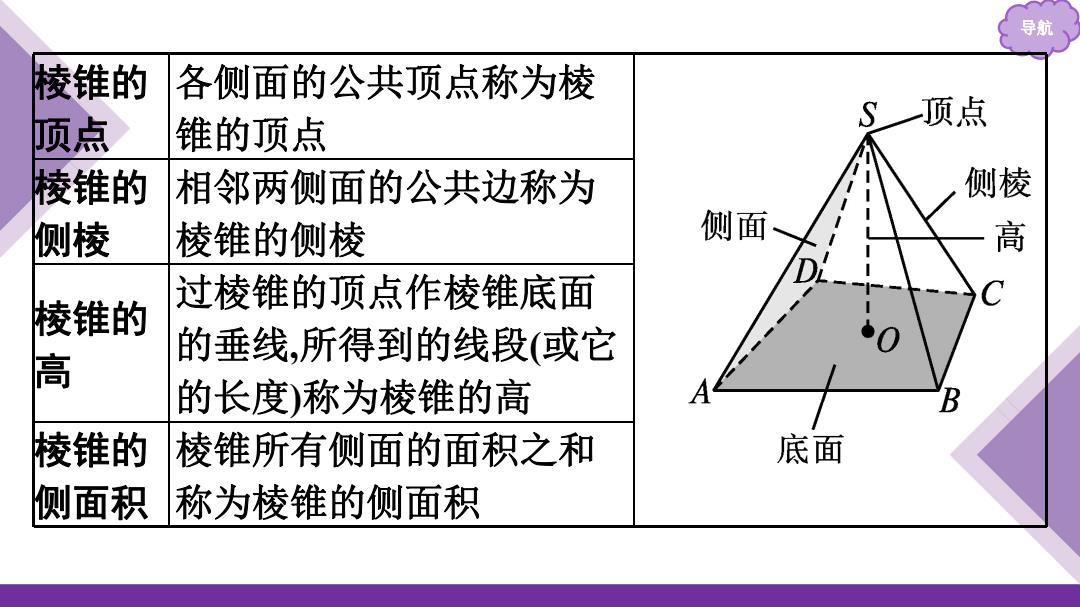
导航 棱锥的 各侧面的公共顶点称为棱 顶点 锥的顶点 S一顶点 棱锥的 相邻两侧面的公共边称为 侧棱 侧棱 棱锥的侧棱 侧面 高 过棱锥的顶点作棱锥底面 棱锥的 的垂线,所得到的线段(或它 高 的长度)称为棱锥的高 棱锥的 棱锥所有侧面的面积之和 底面 侧面积 称为棱锥的侧面积
导航 棱锥的 顶点 各侧面的公共顶点称为棱 锥的顶点 棱锥的 侧棱 相邻两侧面的公共边称为 棱锥的侧棱 棱锥的 高 过棱锥的顶点作棱锥底面 的垂线,所得到的线段(或它 的长度)称为棱锥的高 棱锥的 侧面积 棱锥所有侧面的面积之和 称为棱锥的侧面积
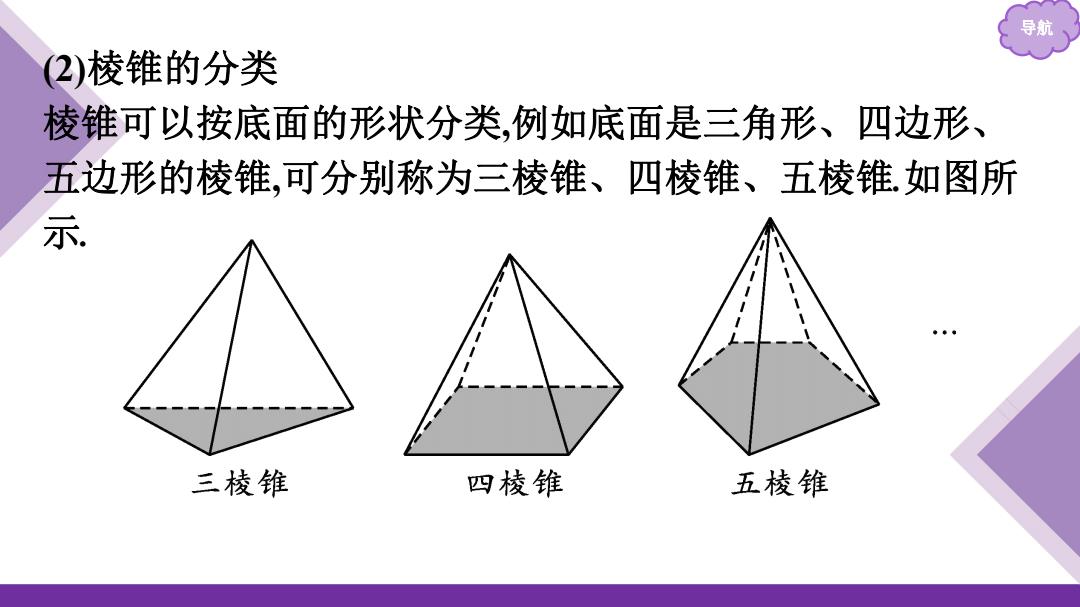
导航 (2)棱锥的分类 棱锥可以按底面的形状分类,例如底面是三角形、四边形、 五边形的棱锥,可分别称为三棱锥、四棱锥、五棱锥如图所 示 三棱锥 四棱锥 五棱锥
导航 (2)棱锥的分类 棱锥可以按底面的形状分类,例如底面是三角形、四边形、 五边形的棱锥,可分别称为三棱锥、四棱锥、五棱锥.如图所 示

导航 (3)棱锥的表示 棱锥可以用顶点与底面各顶点的字母来表示 (4)正棱锥及相关概念 如果棱锥的底面是 ,且棱锥的顶点与底面 的连 线垂直于底面,则称这个棱锥为正棱锥正棱锥的侧面都全等, 而且都是 三角形,这些等腰三角形底边上的高也都相等 称为棱锥的
导航 (3)棱锥的表示 棱锥可以用顶点与底面各顶点的字母来表示. (4)正棱锥及相关概念 如果棱锥的底面是正多边形 ,且棱锥的顶点与底面中心的连 线垂直于底面,则称这个棱锥为正棱锥.正棱锥的侧面都全等, 而且都是等腰三角形,这些等腰三角形底边上的高也都相等, 称为棱锥的斜高

导航 3.做一做: 命题:①底面是正多边形的棱锥一定是正棱锥;②所有侧棱长 都相等的棱锥一定是正棱锥;③正棱锥的棱长都相等.其中正 确命题的个数为(): A.0B.1C.2D.3
导航 3.做一做: 命题:①底面是正多边形的棱锥一定是正棱锥;②所有侧棱长 都相等的棱锥一定是正棱锥;③正棱锥的棱长都相等.其中正 确命题的个数为( ). A.0 B.1 C.2 D.3

导期 解析:由正棱锥的定义可知①错误; 侧棱长都相等时,底面可以不是正多边形,比如一个三棱锥,侧 棱长都相等,但侧棱的夹角不相等,因此底面边长不相等,不是 正三棱锥,所以②错误; 棱锥的棱包括侧棱和底面的边,正棱锥的侧棱长都相等,底面 边长都相等,但侧棱长和底面边长可能不相等,所以③错误 综上,选A 答案:A
导航 解析:由正棱锥的定义可知①错误; 侧棱长都相等时,底面可以不是正多边形,比如一个三棱锥,侧 棱长都相等,但侧棱的夹角不相等,因此底面边长不相等,不是 正三棱锥,所以②错误; 棱锥的棱包括侧棱和底面的边,正棱锥的侧棱长都相等,底面 边长都相等,但侧棱长和底面边长可能不相等,所以③错误. 综上,选A. 答案:A