《线性代数》课程教学资源（PPT课件讲稿）第二章 矩阵与向量 2-1 消元法与矩阵的初等变换

第二章矩阵与向量 X1 =-1 1 X2 =-2 3 4=2

第二章 矩阵与向量 3 1 32 1 + 3 13 − 12 − 124 12 2 xxx  = −  = −  =

第二章矩阵与向量 引例2 某班级同学早餐情况 姓名 馒头 包子 鸡蛋 稀饭 特朗普 2 3 1 0 金正恩 1 1 0 1 武契奇 3 0 1 2 为了方便，常用下面的数表表示： 2 3 0 这个表非常清晰的显示了同学们 1 1 0 的早餐情况 3 012

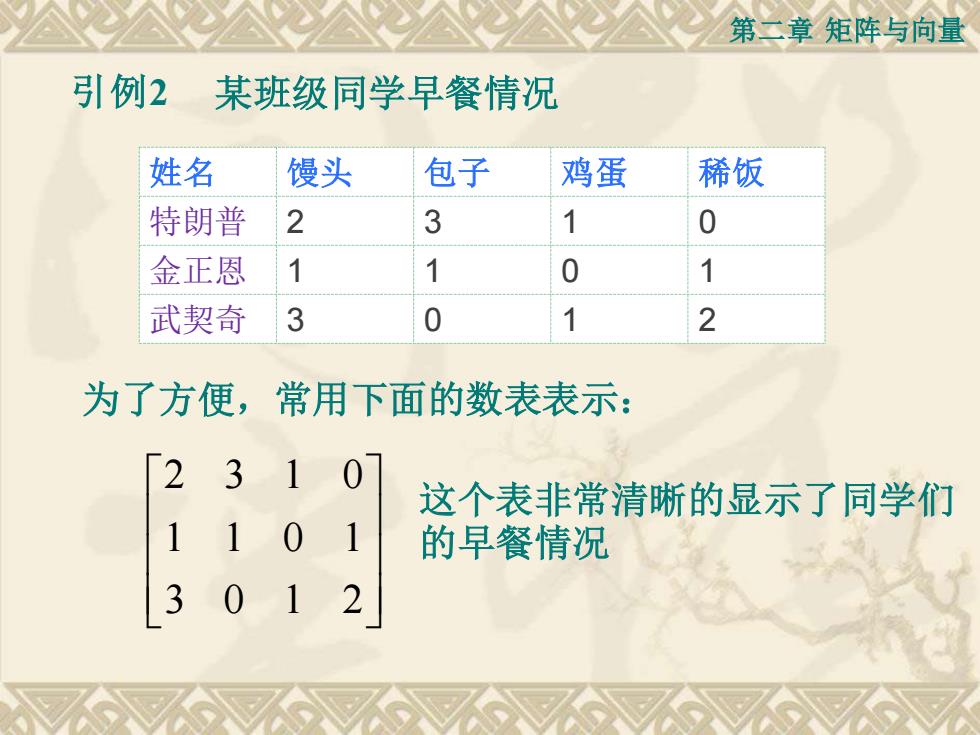
第二章 矩阵与向量 引例2 某班级同学早餐情况 姓名 馒头 包子 鸡蛋 稀饭 特朗普 2 3 1 0 金正恩 1 1 0 1 武契奇 3 0 1 2 为了方便，常用下面的数表表示： 2 3 1 0 1 1 0 1 3 0 1 2           这个表非常清晰的显示了同学们 的早餐情况

第二章矩阵与向量 二、矩阵 1、矩阵的定义 定义2.1.1由m×n个数a(i=1,2,m;j=1,2,.,n) 排成的m行n列的数表 11 2 A= L21 2 : 0m2 称为m×n矩阵.简称m×n阵

第二章 矩阵与向量 由 m n 个数 m n a (i m j n) ij = 1,2,  , ; = 1,2,  , 11 12 1 21 22 2 1 2 n n m m mn a a a a a a A a a a       =       称为 mn 矩阵.简称 m  n 阵. 定义2.1.1 排成的 行 列的数表 二、矩阵 1、矩阵的定义

第二章矩阵与向量 这m×个数称为4的元素，简称为元，叫做矩阵A 的第行第列元素.元素是实数的矩阵称为实矩阵， 元素是复数的矩阵称为复矩阵 矩阵简记为A=Axn=(an=(a, 行数与列数都等于n的矩阵，称为n阶方阵. 035 例如 9 6 43 是一个2×4实矩阵， 62i 2 2 2 是一个3阶方阵 2 2 2

第二章 矩阵与向量 矩阵简记为 ( ) ( ). ij m n A = Am n = aij = a   , , . m n A a A ij i j 这  个数称为 的 简称为 叫做矩阵 的第 行第 素 元 列元素 元 元素是实数的矩阵称为实矩阵, 元素是复数的矩阵称为复矩阵. 行数与列数都等于 n 的矩阵 A ，称为 n 阶方阵. 例如 1 0 3 5 9 6 4 3       − 是一个 24 实矩阵, 13 6 2 2 2 2 2 2 2  i         是一个3 阶方阵

第二章矩阵与向量 例如，一般元线性方程组 411X1+012X2+.+41mXn=b1 02IX1+22X2+.+02mxn=b2 (8) amx+am2x2+.+amnxn=bm 的未知量的系数可以用矩阵A=(a)mxm来表示， 此时称A为方程组的系数矩阵

第二章 矩阵与向量 例如，一般n元线性方程组 此时称A为方程组的系数矩阵. ( ) 的未知量的系数可以用矩阵 A a = ij m n 来表示， 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 . . (8) . . n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b  + + + =   + + + =    + + + = 