
第二章晶体振荡器概述 当在谐振模式i发生振动时,其他串联RLC支路可以忽略。由于晶体的高Q值, 即使晶体两端的电压存在很强的失真,流过支路的电流仍是很好的正弦信号。 从图2-2中可以看到,晶体存在两个振荡频率,分别是它的串联谐振频率f和 并联谐振频率f。 1 f3= (2.4) 2TTLCa o=- (2.5) CCo +Co 晶体的机械振动频率也即本振频率为,它只同晶体本身的参数有关,同供压 波动及其他外部影响相对无关。我们希望电路的工作频率越接近本振频率越好, 因为并联谐振频率同外部引入的电容相关,是一个不可控制的量。 谐振器的串联阻抗为 Z@)=R+juL+=R+1“2-w iwC:W2) (2.6) jwCsi 把振荡器的“牵引”定义为相对于wm的相对频率偏移,即p=(w-wm)lwmi。由 于谐振时的频率w非常接近wmi,故p<1,将牵引系数p公式代入式(2.6)得 到, Zmi(w)≈R+j 2p Csi (2.7) 25MHz晶体的参数值如表2-1所示。根据图2-2的等效模型和式(2.6)的 阻抗表达式,可以得到晶体阻抗随频率的变化曲线,如图2-3所示。 表2-125MHz晶体参数 Rs Ls Cs Co 40ΩMAX 13.0mH±25% 2.8ff±20% 0.9pF±20% 当频率由低到高变化时,晶体大致可以看作一个电容,其阻抗随频率的升 高而降低。但是在谐振频率附近,情况发生变化。在谐振频率处,晶体呈现90 度的相移特性,因此可以把晶体看作一个感性元件,当我们的外接电路呈容性 时,发生振荡。这种振荡器的电路图如图2-4所示,将一个(非线性)电路连接 到谐振器上,这个电路的作用是提供一个负阻,能量以谐振器的谐振频率(或者 很接近谐振频率)在电路和谐振器之间无损地来回传递,从而维持这个频率的振 荡。该电路的阻抗分离模型见图2-5。 >
第二章 晶体振荡器概述 7 当在谐振模式 i 发生振动时,其他串联 RLC 支路可以忽略。由于晶体的高 Q 值, 即使晶体两端的电压存在很强的失真,流过支路的电流 ii 仍是很好的正弦信号。 从图 2-2 中可以看到,晶体存在两个振荡频率,分别是它的串联谐振频率 fs和 并联谐振频率 fp。 s si si 1 2π f L C = (2.4) p si 0 si si 0 1 2π f C C L C C = + (2.5) 晶体的机械振动频率也即本振频率为 fs,它只同晶体本身的参数有关,同供压 波动及其他外部影响相对无关。我们希望电路的工作频率越接近本振频率越好, 因为并联谐振频率 fp同外部引入的电容相关,是一个不可控制的量。 谐振器的串联阻抗为 2 2 mi mi si si si 2 si si mi 1 1 () j ( ) j j ω ω Z ω R ωL R ωC ωC ω − =+ + =+ (2.6) 把振荡器的“牵引”定义为相对于 ωmi 的相对频率偏移,即 p=(ω-ωmi)/ωmi。由 于谐振时的频率 ω 非常接近 ωmi,故 p<<1,将牵引系数 p 公式代入式(2.6)得 到, mi si si 2 () j p Z ω R ωC ≈ + (2.7) 25 MHz 晶体的参数值如表 2-1 所示。根据图 2-2 的等效模型和式(2.6)的 阻抗表达式,可以得到晶体阻抗随频率的变化曲线,如图 2-3 所示。 表 2-1 25 MHz 晶体参数 Rs Ls Cs C0 40 Ω MAX 13.0 mH ± 25% 2.8 fF ± 20% 0.9 pF ± 20% 当频率由低到高变化时,晶体大致可以看作一个电容,其阻抗随频率的升 高而降低。但是在谐振频率附近,情况发生变化。在谐振频率处,晶体呈现 90 度的相移特性,因此可以把晶体看作一个感性元件,当我们的外接电路呈容性 时,发生振荡。这种振荡器的电路图如图 2-4 所示,将一个(非线性)电路连接 到谐振器上,这个电路的作用是提供一个负阻,能量以谐振器的谐振频率(或者 很接近谐振频率)在电路和谐振器之间无损地来回传递,从而维持这个频率的振 荡。该电路的阻抗分离模型见图 2-5
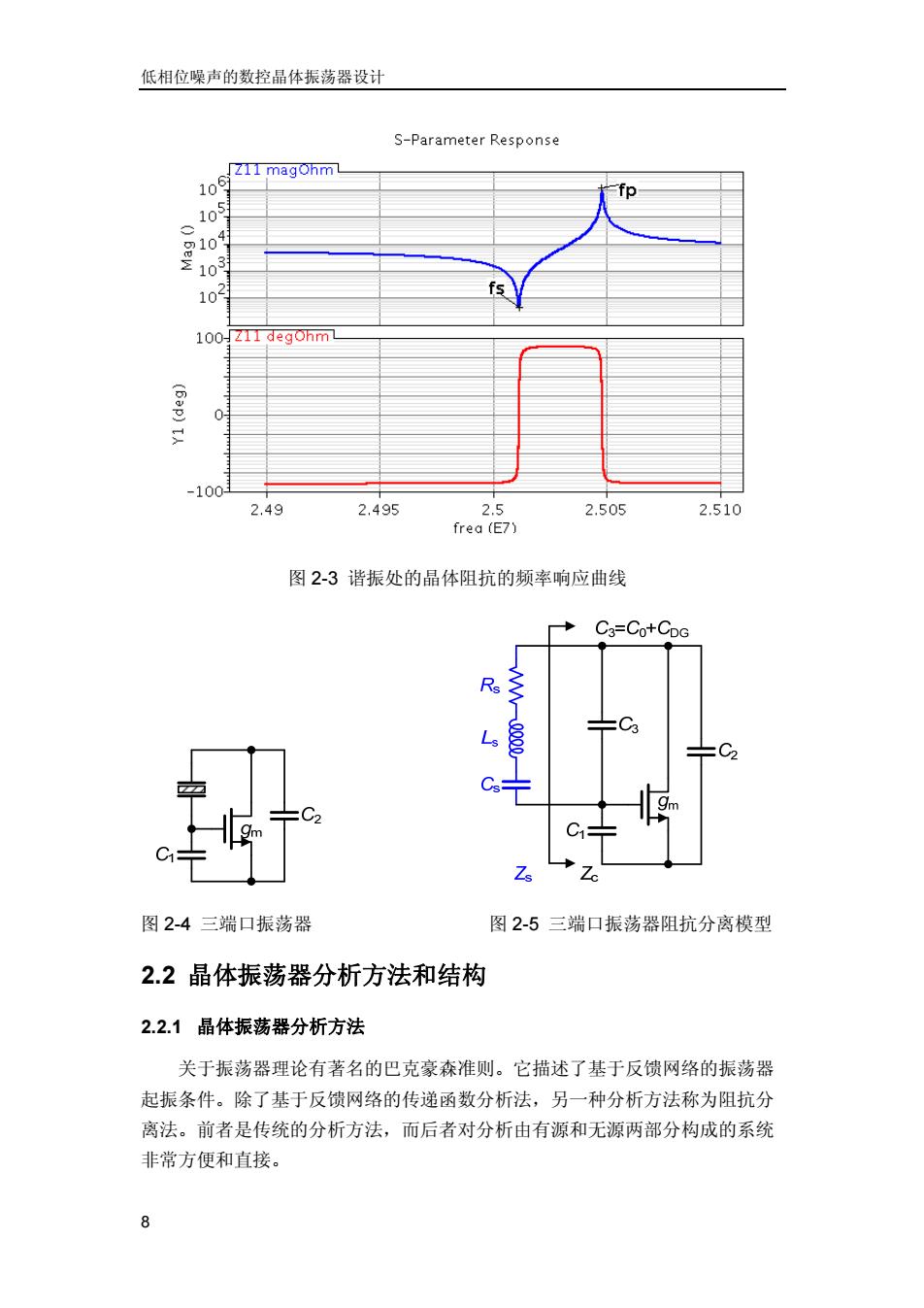
低相位噪声的数控晶体振荡器设计 S-Parameter Response Z11 magohml 106 1 4 10 2 10 100Z11 degohml Q -100 2.49 2.495 2.5 2.505 2.510 frea (E7) 图2-3谐振处的晶体阻抗的频率响应曲线 C3=Co+CDG R 1C3 C C1= Z 图2-4三端口振荡器 图2-5三端口振荡器阻抗分离模型 2.2晶体振荡器分析方法和结构 2.2.1晶体振荡器分析方法 关于振荡器理论有著名的巴克豪森准则。它描述了基于反馈网络的振荡器 起振条件。除了基于反馈网络的传递函数分析法,另一种分析方法称为阻抗分 离法。前者是传统的分析方法,而后者对分析由有源和无源两部分构成的系统 非常方便和直接。 8
低相位噪声的数控晶体振荡器设计 8 图 2-3 谐振处的晶体阻抗的频率响应曲线 图 2-4 三端口振荡器 图 2-5 三端口振荡器阻抗分离模型 2.2 晶体振荡器分析方法和结构 2.2.1 晶体振荡器分析方法 关于振荡器理论有著名的巴克豪森准则。它描述了基于反馈网络的振荡器 起振条件。除了基于反馈网络的传递函数分析法,另一种分析方法称为阻抗分 离法。前者是传统的分析方法,而后者对分析由有源和无源两部分构成的系统 非常方便和直接

第二章晶体振荡器概述 a)传递函数分析法 Vin Vout F(jw) 图2-6振荡器的正反馈模型 传递函数分析法是分析反馈网络的经典方法。如图2-6所示,要想电路振 荡,在输入n为零的情况下,误差反馈信号经过环路AGw)F(j后的信号 4必须维持原信号的大小。放大网络为非线性有源网络,反馈网络为线性无源 网络,具有选频特性。输入输出满足: Vu=A(jwV。 (2.8) V:=F(jw)v=F(jw)A(jw)v (2.9) VL=A(jw)F(jw) (2.10) 据此,该系统起振的巴克豪森必要条件为: =A(jw)F(jw)≥1 (2.11) =中A+中=0 振荡电路在内部噪声干扰下启动,输出振幅逐渐增大,最后在电路非线性作用 下,环路增益降为1维持振荡。即,如果反馈网络F(ω)起衰减信号的作用, 那么AGw必然要放大信号:如果放大器A(jw)呈容性,那么反馈网络F(ω)必 然呈感性。目前,放大器都呈容性特征,那意味着需要一个感性的反馈网络来 构建起振荡系统。 b)阻抗分离法 将放大器A(Gw)用电路阻抗Zr代替,反馈网络用谐振器的阻抗Zes代替, 得到图2-7。由于振荡发生于系统内部,不从外部获取电流,即系统的输入导 纳为零: Yres +Ycir =0 (2.12) ⊙
第二章 晶体振荡器概述 9 a) 传递函数分析法 图 2-6 振荡器的正反馈模型 传递函数分析法是分析反馈网络的经典方法。如图 2-6 所示,要想电路振 荡,在输入 vin 为零的情况下,误差反馈信号 vε 经过环路 A(jω)F(jω)后的信号 vf 必须维持原信号的大小。放大网络为非线性有源网络,反馈网络为线性无源 网络,具有选频特性。输入输出满足: out ε v A = (j ) ω v (2.8) f out ε v F = = (j ) (j ) (j ) ω v F ω A ω v (2.9) f ε (j ) (j ) v v = A ω F ω (2.10) 据此,该系统起振的巴克豪森必要条件为: f ε f A F ε (j ) (j ) 1 v =0 v v A ω F ω v Φ Φ = ≥ ⎧ ⎫ ⎨ ⎬ = + ⎩ ⎭ D (2.11) 振荡电路在内部噪声干扰下启动,输出振幅逐渐增大,最后在电路非线性作用 下,环路增益降为 1 维持振荡。即,如果反馈网络 F(jω)起衰减信号的作用, 那么 A(jω)必然要放大信号;如果放大器 A(jω)呈容性,那么反馈网络 F(jω)必 然呈感性。目前,放大器都呈容性特征,那意味着需要一个感性的反馈网络来 构建起振荡系统。 b) 阻抗分离法 将放大器 A(jω)用电路阻抗 Zcir代替,反馈网络用谐振器的阻抗 Zres 代替, 得到图 2-7。由于振荡发生于系统内部,不从外部获取电流,即系统的输入导 纳为零: Y Y res cir + = 0 (2.12)

低相位噪声的数控晶体振荡器设计 Ycir+Yres 图2-7振荡器的负阻模型 1+1=0 (2.13) Zes+Z。=0 (2.14) ZresZcir 进一步推导有 Re(Zres+Zdr)=0 (2.15) Im(Zes +Zcir)=0 (2.16) 式(2.15)和(2.16)给出了谐振时的条件,谐振器的阻抗和电路阻抗之和为零。传 递函数分析法从幅度和相位角度描述振荡条件,阻抗分离法则从实虚部角度描 述了振荡条件。 针对不同的振荡电路,两种分析方法各有特点。基于反馈网络的传递函数 分析利用其相位平衡条件可以计算振荡频率,阻抗分离的分析方法可以快速得 到满足系统振荡的最小增益。 2.2.2CMOS晶体振荡器结构 晶体振荡器可以分为并联谐振和串联谐振两大类。串联谐振利用晶体在串 联谐振处的电抗为零,呈现短路特性,使电路满足振荡条件。并联谐振利用晶 体在并联谐振时呈现的感性特征,将其视作电感,从而和外部的电容构成电容 三点式振荡器。由于该等效电感具有极高的Q值,因此能获得频率纯净的振荡 信号。大部分晶体振荡器都采用电容三点式并联谐振以利用晶体的高Q值感 抗。 CMOS工艺下的单管有源器件足以提供有效的增益使晶振起振。事实上, 根据器件偏置的不同,交流接地点的不同,单管晶体振荡电路形成了如图2-8 所示的三种结构,分别称为Pierce,Colpitts和Santos结构。 Pierce结构中电容一端接地,频率调谐可以同时施加于C1和C2两个电容 阵列上,电路的实现相对简单。Pierce结构通常用一对偏置于饱和区的MOS 管反相器实现,由于反相器的AB类工作特性,电流正比于振荡幅度,因此会 10
低相位噪声的数控晶体振荡器设计 10 图 2-7 振荡器的负阻模型 res cir 1 1 0 Z Z + = (2.13) res cir res cir 0 Z Z Z Z + = (2.14) 进一步推导有 Re( ) 0 Z Z res cir + = (2.15) res cir Im( ) 0 Z Z+ = (2.16) 式(2.15)和(2.16)给出了谐振时的条件,谐振器的阻抗和电路阻抗之和为零。传 递函数分析法从幅度和相位角度描述振荡条件,阻抗分离法则从实虚部角度描 述了振荡条件。 针对不同的振荡电路,两种分析方法各有特点。基于反馈网络的传递函数 分析利用其相位平衡条件可以计算振荡频率,阻抗分离的分析方法可以快速得 到满足系统振荡的最小增益。 2.2.2 CMOS 晶体振荡器结构 晶体振荡器可以分为并联谐振和串联谐振两大类。串联谐振利用晶体在串 联谐振处的电抗为零,呈现短路特性,使电路满足振荡条件。并联谐振利用晶 体在并联谐振时呈现的感性特征,将其视作电感,从而和外部的电容构成电容 三点式振荡器。由于该等效电感具有极高的 Q 值,因此能获得频率纯净的振荡 信号。大部分晶体振荡器都采用电容三点式并联谐振以利用晶体的高 Q 值感 抗。 CMOS 工艺下的单管有源器件足以提供有效的增益使晶振起振。事实上, 根据器件偏置的不同,交流接地点的不同,单管晶体振荡电路形成了如图 2-8 所示的三种结构,分别称为 Pierce,Colpitts 和 Santos 结构。 Pierce 结构中电容一端接地,频率调谐可以同时施加于 C1和 C2两个电容 阵列上,电路的实现相对简单。Pierce 结构通常用一对偏置于饱和区的 MOS 管反相器实现,由于反相器的 AB 类工作特性,电流正比于振荡幅度,因此会
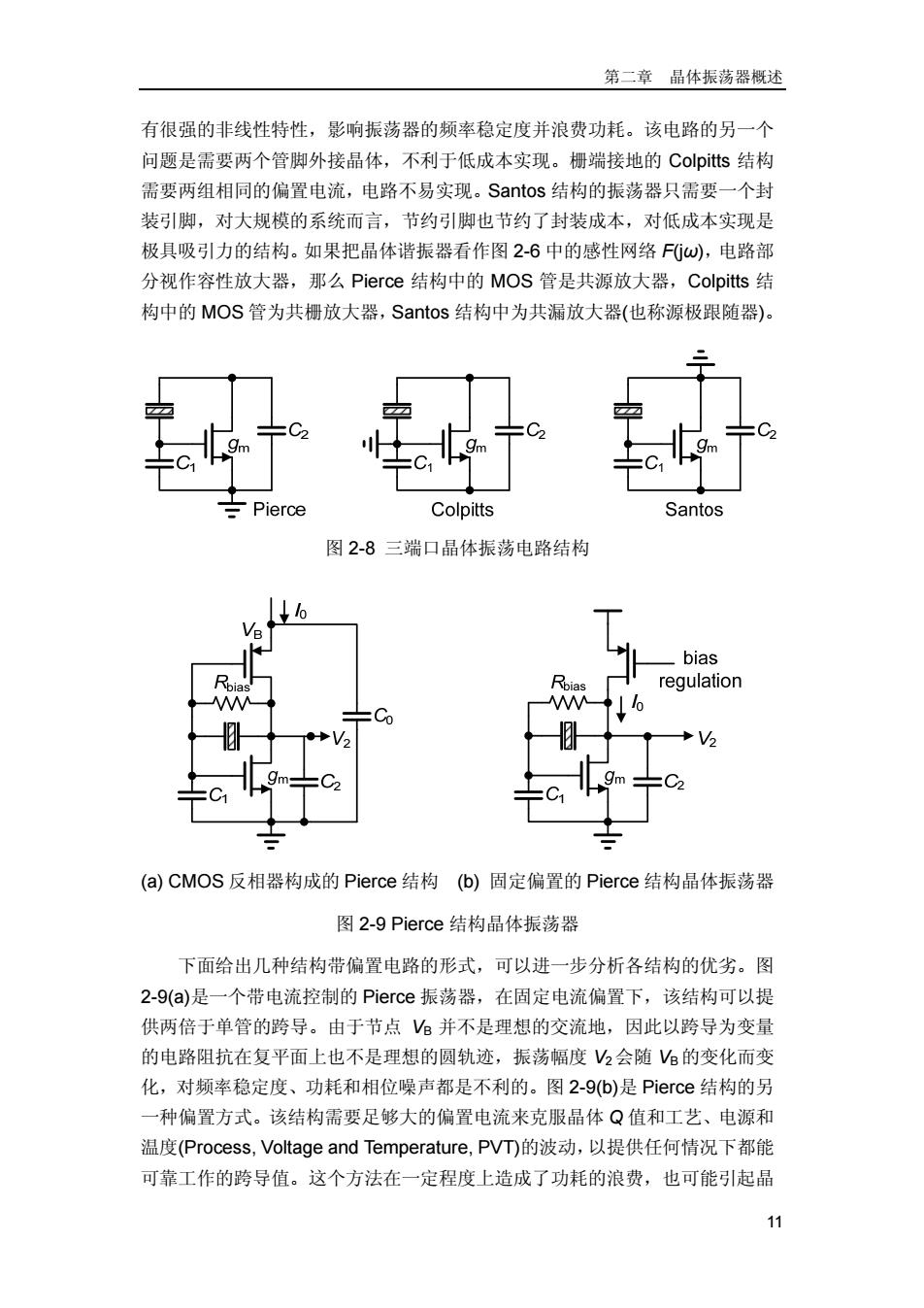
第二章晶体振荡器概述 有很强的非线性特性,影响振荡器的频率稳定度并浪费功耗。该电路的另一个 问题是需要两个管脚外接晶体,不利于低成本实现。栅端接地的Colpitts结构 需要两组相同的偏置电流,电路不易实现。Santos结构的振荡器只需要一个封 装引脚,对大规模的系统而言,节约引脚也节约了封装成本,对低成本实现是 极具吸引力的结构。如果把晶体谐振器看作图2-6中的感性网络Fω),电路部 分视作容性放大器,那么Pierce结构中的MOS管是共源放大器,Colpitts结 构中的MOS管为共栅放大器,Santos结构中为共漏放大器(也称源极跟随器) -Pierce Colpitts Santos 图2-8三端口晶体振荡电路结构 bias Rpias Rbias regulation M =C0 V2 V gm (a)CMOS反相器构成的Pierce结构(b)固定偏置的Pierce结构晶体振荡器 图2-9 Pierce结构晶体振荡器 下面给出几种结构带偏置电路的形式,可以进一步分析各结构的优劣。图 2-9(a)是一个带电流控制的Pierce振荡器,在固定电流偏置下,该结构可以提 供两倍于单管的跨导。由于节点V%并不是理想的交流地,因此以跨导为变量 的电路阻抗在复平面上也不是理想的圆轨迹,振荡幅度V2会随Ve的变化而变 化,对频率稳定度、功耗和相位噪声都是不利的。图2-9(b)是Pierce结构的另 一种偏置方式。该结构需要足够大的偏置电流来克服晶体Q值和工艺、电源和 温度(Process,Voltage and Temperature,PVT)的波动,以提供任何情况下都能 可靠工作的跨导值。这个方法在一定程度上造成了功耗的浪费,也可能引起晶 11
第二章 晶体振荡器概述 11 有很强的非线性特性,影响振荡器的频率稳定度并浪费功耗。该电路的另一个 问题是需要两个管脚外接晶体,不利于低成本实现。栅端接地的 Colpitts 结构 需要两组相同的偏置电流,电路不易实现。Santos 结构的振荡器只需要一个封 装引脚,对大规模的系统而言,节约引脚也节约了封装成本,对低成本实现是 极具吸引力的结构。如果把晶体谐振器看作图 2-6 中的感性网络 F(jω),电路部 分视作容性放大器,那么 Pierce 结构中的 MOS 管是共源放大器,Colpitts 结 构中的 MOS 管为共栅放大器,Santos 结构中为共漏放大器(也称源极跟随器)。 图 2-8 三端口晶体振荡电路结构 (a) CMOS 反相器构成的 Pierce 结构 (b) 固定偏置的 Pierce 结构晶体振荡器 图 2-9 Pierce 结构晶体振荡器 下面给出几种结构带偏置电路的形式,可以进一步分析各结构的优劣。图 2-9(a)是一个带电流控制的 Pierce 振荡器,在固定电流偏置下,该结构可以提 供两倍于单管的跨导。由于节点 VB 并不是理想的交流地,因此以跨导为变量 的电路阻抗在复平面上也不是理想的圆轨迹,振荡幅度 V2会随 VB的变化而变 化,对频率稳定度、功耗和相位噪声都是不利的。图 2-9(b)是 Pierce 结构的另 一种偏置方式。该结构需要足够大的偏置电流来克服晶体 Q 值和工艺、电源和 温度(Process, Voltage and Temperature, PVT)的波动,以提供任何情况下都能 可靠工作的跨导值。这个方法在一定程度上造成了功耗的浪费,也可能引起晶