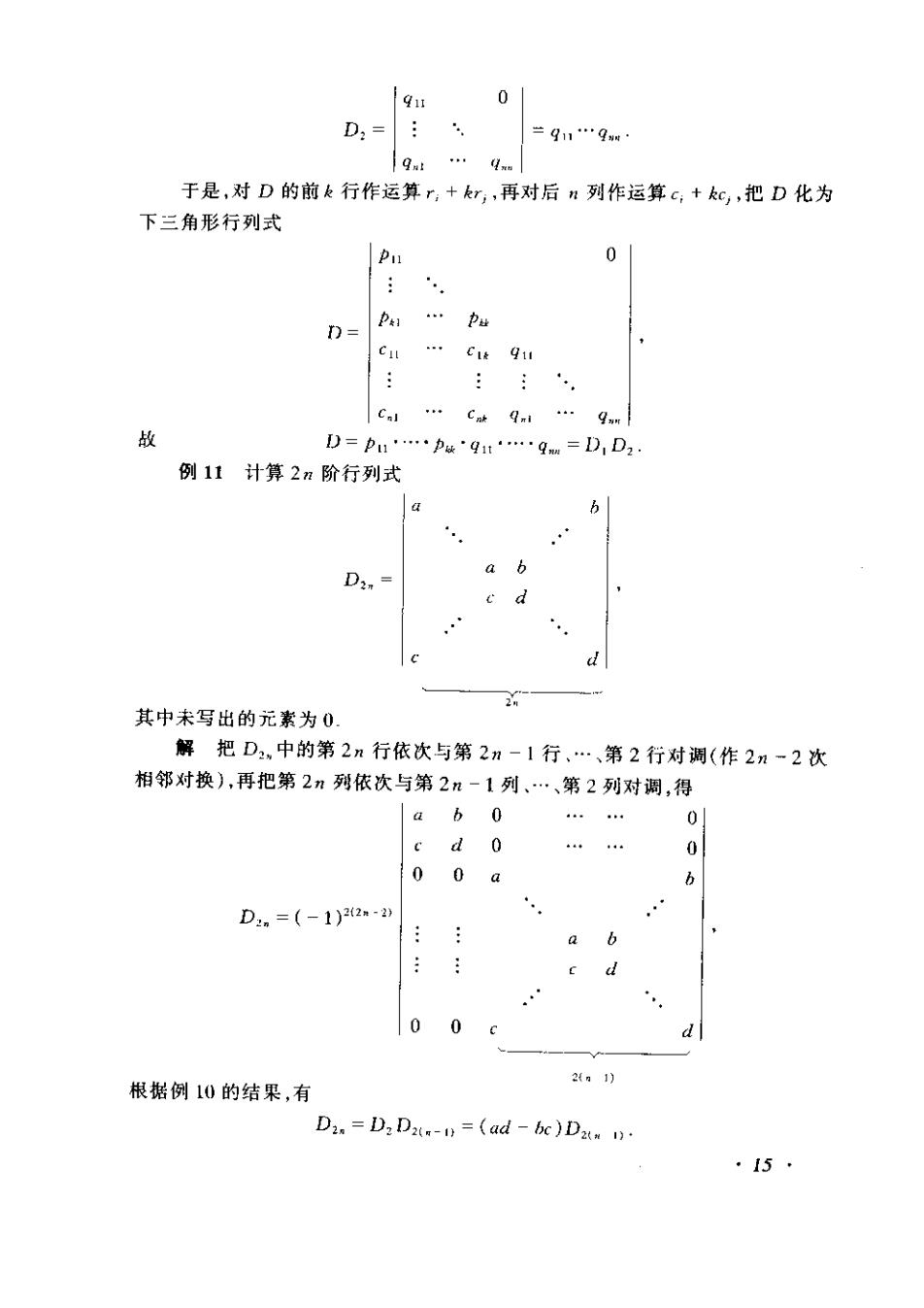
9 0 D=: =911.9m 于是,对D的前行作运算,+,再对后n列作运算c,+kc,把D化为 下三角形行列式 Pn 0 c. c491u 故 D=pu.pk91t.gw=D1D2 例11计算2n阶行列式 D2, 2 其中未写出的元素为0. 解把D2,中的第2n行依次与第2n-1行、.、第2行对调(作2n一2次 相邻对换),再把第2n列依次与第2n一1列、·、第2列对调,得 a b 0 . 0 c d 0 44 0 00a b D,=(-1)22-20 . 6 d 0 0 c d 21) 根据例10的结果,有 Di.=D:Da-1)=(ad-be)D. ·15·

以此作递推公式,即得 D3=(ad-bc)'Dx==(ad-be)"D2 =(ad-bc)". §6行列式按行(列)展开 一般说来,低阶行列式的计算比高阶行列式的计算要简便,于是,我们自然 地考虑用低阶行列式来表示高阶行列式的问题.为此,先引进余子式和代数余子 式的概念 在阶行列式中,把(i,j)元a,所在的第;行和第j列划去后.留下来的 ”1阶行列式叫做(i,)元4,的余子式,记作M:记 A,=(-1)M, A叫做(i,j)元4,的代数余子式. 例如四阶行剑式 uu anan un D= an a an az 中(3,2)元:2的余子式和代数余子式分别为 Me=a2a4 A=(-1)3M”-M 引理一个n阶行列式,如果其中第i行所有元素除(i,)元au外都为零, 那么这行列式等于au与它的代数余子式的乘积,即 D=auA 证先证(i,)=(1,1)的情形,此时 a10.0 Dja1a:.ae auta.ani 这是例10中当k=1时的特殊情形,按例10的结论,即有 D=a Mn. ·16·

A,=(-1)M,M, 从而 D=A. 耳证一般情形,此时 D0.0 .w 为了利州前面的结果,把D的行列作如下调换:把D的第;行依次与第 ;1行、第i-2行、.、第1行对调,这样数“,就调成(1,j)元,趟换的次数为 ;1.再把第j列依次马与第j-1列,第j-2列、.、第】列对调,这样数“,就调 城(1,1)元,调换的次数为j-1.总之,经i+j·2次调换,把数a,调城(1,1)元 所得的行列式D“(-1)2D=(-1)D,而D,中(1,l)元的余子式就是 D中(:)元的余子式Mm 由于D,的(1,1)元为44,第1行其余元索都为0.利州前面的结果,有 D.=ayM. 子于是 D=(-1)'D1=(-1)'anMn=aA 定理3行列式等于它的任一行(列)的各元素与其对应的代数余子式乘积 之和.即 D=aAa+aA2+.+anAm(i=1,2,.,n). 或 D=a,Ay+aA,+.+anA(j=1.2,.,n) 证 an 12 D=a4+0+.+00+a2+0.0+.+0tan 0 0 0 0 17

aa.a1n +.+00.an 根据引理,即得 D=a1A,+a2Aa+.+aA(i=1,2,.,n) 类似地,若按列证明,可得 D=a1Ay+a2A3+.+awAy(=1,2,.,n). 证毕 这个定理叫做行列式按行(列)展开法则.利用这一法则并结合行列式的性 质,可以简化行列式的计算. 下面用此法则来计算例7的 {3-1 D=-513-4 201-1 1-53-3 保留a,把第3行其余元素变为0,然后按第3行展开: 151-11H D92e, -1113-1 0 01 0 -5-53 0 5 1 1/ 511 =(-1)33 -11 1-1 ratr -620 -5 0 -5-50 =(-1)1*-6 2|4-8 -5 - 0 2=40 -5 例12证明范德蒙德(Vandermonde)行列式 1 1 1 D.=xi x . -. (8) x.x1 其中记号“川”表示全体同类因子的乘积 证用数学归纳法.因为 ·8·

o,刀 所以当n=2时(8)式成立.现在假设(8)式对于n-1阶范德蒙德行列式成立, 要证(8)式对n阶范德蒙德行列式也成立, 为此,设法把D。降阶:从第n行开始,后行减去前行的x,倍,有 1 1 1 1 0 xa-1 I。-xi D,=0x(x-x1) x(). xn(x,-x1) 02(x2-d)x(x3·x).x2(x.-x1) 按第1列展开,并把每列的公因子(x:-x:)提出,就有 x. r D=(r2x)(x-x1)(x“x1) xx2.x-2 上式右端的行列式是n-1阶范德蒙德行列式,按归纳法假设,它等于所有 (r,2,)因子的乘积,其中n≥i>j≥2.故 D.=(-x)(-(x.x)(x,-) =,(x 证毕 例11和例12都是计算n阶行列式.计算n阶行列式,常要使用数学归纳 法,不过在比较简单的情形(如例11),可省略归纳法的叙述格式,但归纳法的主 要步骤是不可省略的.这主要步骤是:导出递推公式(例11中导出D2.=(ad bc)Dw))及检验n=1时结论成立(例11中最后用到D2=ad-bc). 出定理3,还可得下述重要推论. 推论行列式某一行(列)的元素与另一行(列)的对应元素的代数余子式乘 积之和等于零.即 aA,+a2A,:+.+a.An=0,i≠j, a1A,+42,A2i+.+aA=0,i≠j. 证把行列式D=de(a,)按第j行展开,有 ·19