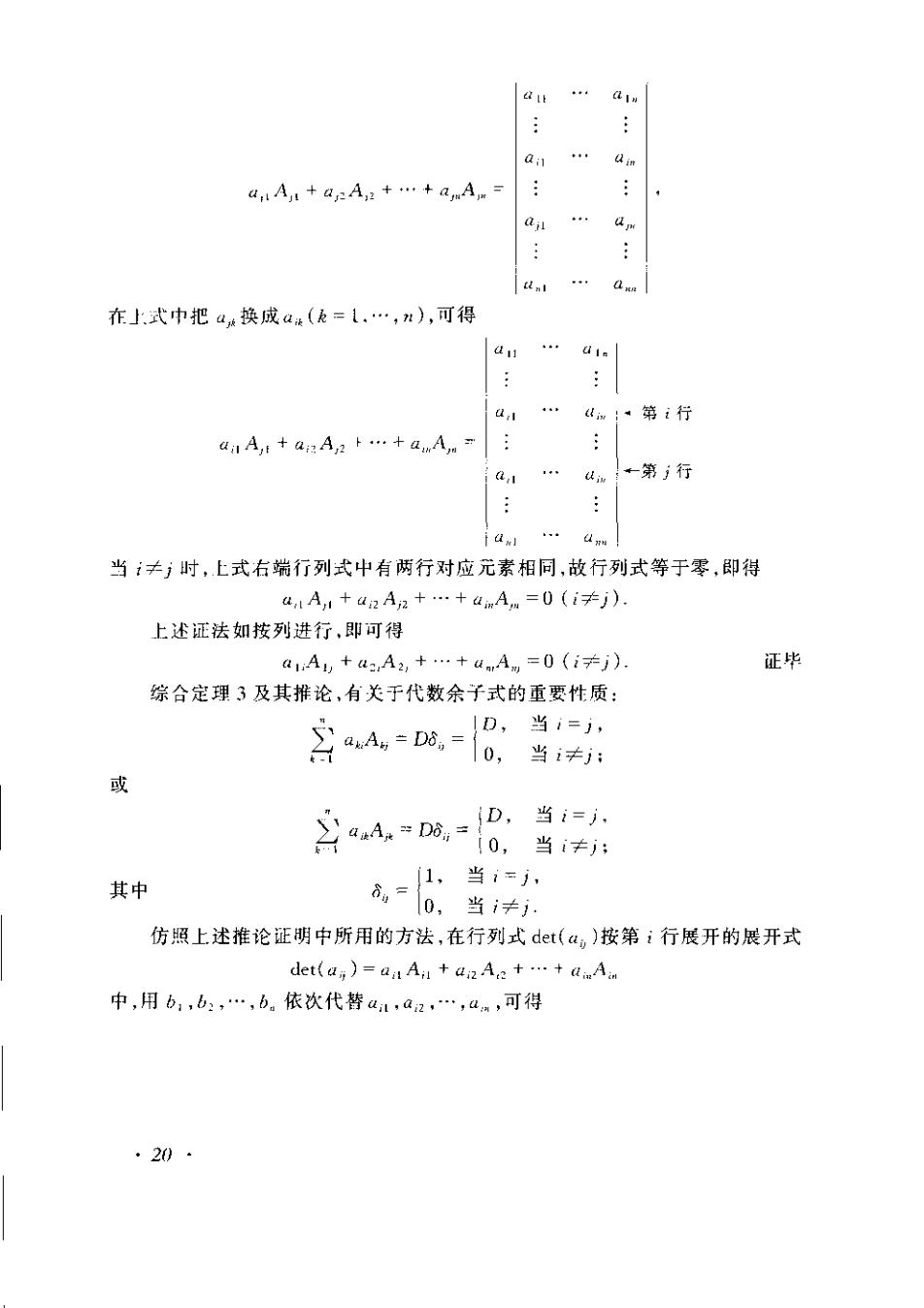
a alAa+aAz+.+anA.= an . 在上式中把4换成(=L.,),可得 an GI. a1.《m!、第i行 a1A:+aA,2卡.+aAr: a1. ,第行 当≠;时,上式右端行列式中有两行对应元素相同,放行列式等于零,即得 a1Al+a2A,2+.+anAm=0(i≠j). 上述证法如按列进行,即可得 a1,A+a:,A2,+.+&Am=0(i≠j) 正毕 综合定理3及其推论,有关于代数余子式的重要性质; 月,=,= D,当i=j, 0,当i≠j: 或 D,当i=j 会aA=,-6当: 其中 1,当i=j, ,=0,当≠ 仿照上述推论证明中所用的方法,在行列式det(a,)按第i行展开的展开式 det(a,)=aaAl+a2Aat.taAn 中,用b,b,.,b。依次代替a,a2,.,a,可得 ·20·

a,L. 6 b. =b,A+b2Ae+.+bAm (9) u:+1.1 其实,把(9)式左端行列式按第:行展开,注意到它的(,)元的代数余子式等于 der(a=)中(i,)元的代数余子式A,(0=1,2,.,n),也可知(9)式成立 类似地,州,.,bn代替det(a,)中的第)列,可得 . =b1A,卡b,A,1.tbA al.a-lh。a-.a (10) 例13设 3-52 1 1105 -1313 2 -4-1-3 D的(i,)元的余子式和代数余子式依次记作M,和A,求 An+A+A+AMn+Ma M+Ma. 解按(9)式可知A:+A2+A+A,等于用1,1,1,1代替D的第1行 所得的行列式,即 1 11 1 1 0-5:+ 10 A,+A2+A3+A4= -1 3 1 3r1-1 -2 20 2 2-4-1-3 1-10 11-5 12-51 -2224-20 1-1 0 10 0 2.5 24 按(10)式可知 M11M2:+M1+M4=A:-A1+A-A4 ·21·

1 -5 2 1 1-52 1 1 0 -5 1 10 -5 3 1 31 3 -4 -1 -3 0 -10 0 12 .10 =(1)-10-5 12r3 -51 10-5=0. 11 3 11 3 §7 克拉默法则 含有n个未知数11,x2,.,x。的n个线性方程的方程组 an+a++aim=b1 anz+anx+.+az=b:, (11) ax,十a2x+.+aw广=b 与二、三元线性方程组相类似,它的解可以用n阶行列式表示,即有 克拉默法则如果线性方程组(1)的系数行列式不等于零,即 au.a1n D= :≠0. a.a 那么,方程组(11)有惟一解 D D. x=D,x=D.,x,=D (12) 其中D,(=1,2,·,n)是把系数行列式D中第;列的元素用方程组右端的常 数项代替后所得到的n阶行列式,即 41 D,=: al.aay1b。am,.am 这个法则的证明在第二章中给出.注意这里的D,有展开式(10) 例14解线性方程组 「2x1+x-5x+x4=8, x1-3x2 -6.x4=9, 2x:-x3+2x4=-5, x1+4x2-7x3+6.x1=0. ·22·
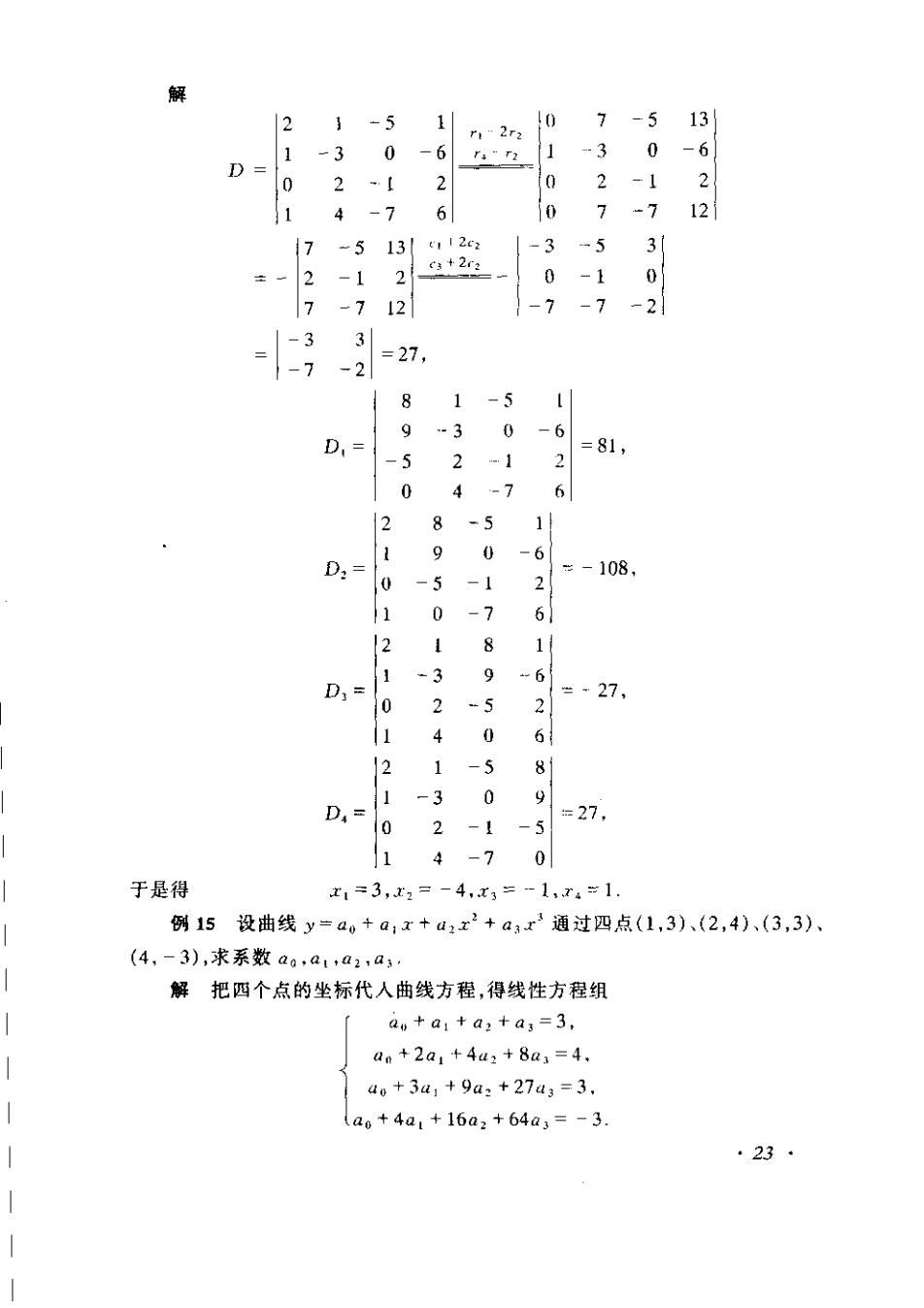
解 1-5 r12r2 0 7-5 13 -3 0 3 0 -6 D= 6/ 2 2 1 6 27 1 7 1 -5 13 C342r: 27 1 0 -1 0 1 -2 八1 =27, 8 1 -5 D,= 9 .3 6 =81 -5 2 1 2 0 ~ 6 2 8 5 1 1 9 0 -6 D:= 0 -5 -1 =-108 0 -7 6 8 1 D1= 1 3 9 -5 =-27, 2 2 4 0 6 12 1 5 81 1-3 0 D4= o 2 -1 -5 =27, 1 4 -7 0 于是得 x1=3,x2=-4,x3=-1,74=1 例15设曲线y=a0+a1x+a2x2+aax3通过四点(1,3)、(2,4)、(3,3) (4,-3),求系数a0,a1,a2a 解把四个点的坐标代人曲线方程,得线性方程组 aw+a1+a2+a,=3, ae+2a1+4a2+8a1=4. 4。+3a1+9a+27a:=3, (a6+4a1+16a2+64a3=-3. ·23·

其系数矿划式 1111 D=?48 13927 141664 是,个花德荣德行列式,按例12的结果(例2中范德蒙德行列式取D的形 式)可得 D1.23121=12. 3111 0100 42483r2 -2224 D,: 33927-3 -63618 341664 -1541248 -224 024 =(-1) -6618 0618 151248 -31248 -(-3)24 618 =36: 1 311 1 4 48 D2= =-18: 3927 1-31664 11 31 12 48 D,= =24: 13 327 14-364 11113 124 D.= 139 36. 1416-3 因此,按克拉默法侧得惟一解 au=3,41=-32,a,-2,4,=-1/2, 却曲线方程为 y=3+2r2-分 撇开求解公式(12),克拉默法铡可叙述为下面的定理, ·24·