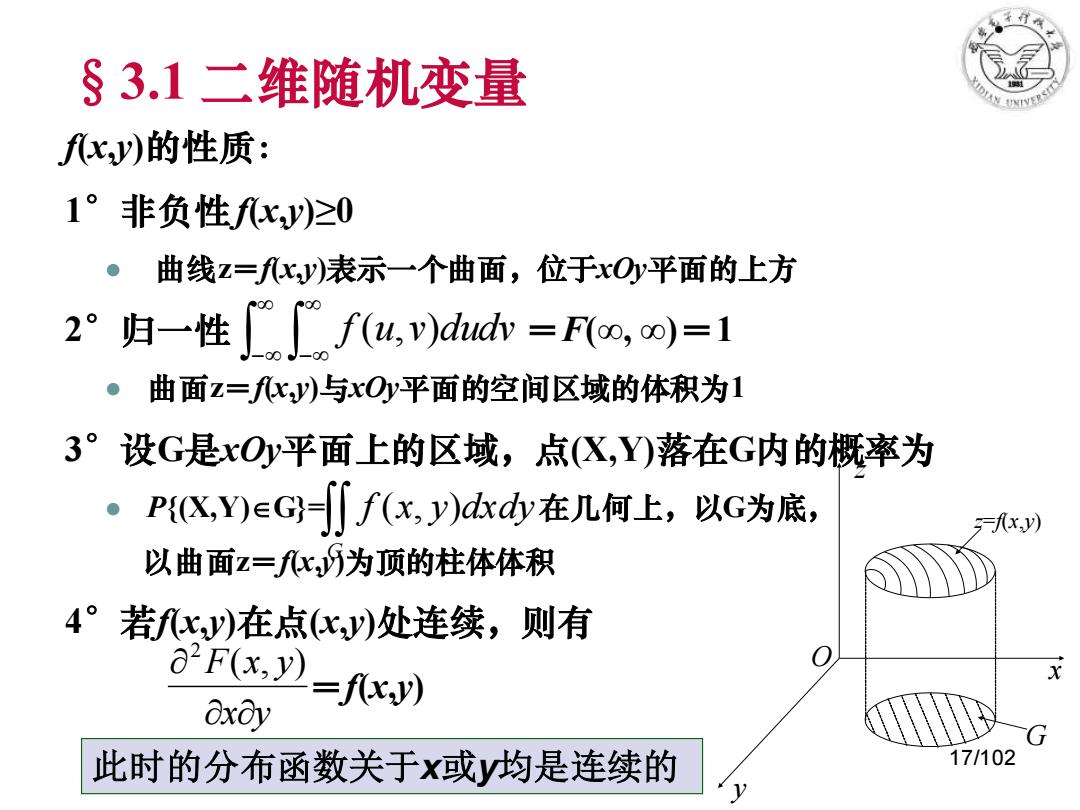
§3.1二维随机变量 fxy)的性质: 1°非负性fx,y)≥0 ●曲线z=fxy)表示一个曲面,位于xOy平面的上方 2°归一性f(u,v)dudv=Fo,o)=1 。曲面z=c,y)与xOy平面的空间区域的体积为1 3°设G是xOy平面上的区域,点(X,Y)落在G内的概率为 ·PX,Y)eGf(x,y)ddy在几何上,以c为底, fx.y) 以曲面z=fc,为顶的柱体体积 4° 若fx,y)在点x,y)处连续,则有 8-F(x, D-fxy) X Oxoy 此时的分布函数关于x或y均是连续的 17/102
17/102 §3.1 二维随机变量 f(x,y)的性质: 1°非负性f(x,y)≥0 ⚫ 曲线z=f(x,y)表示一个曲面,位于xOy平面的上方 2°归一性 =F(∞, ∞)=1 ⚫ 曲面z=f(x,y)与xOy平面的空间区域的体积为1 3°设G是xOy平面上的区域,点(X,Y)落在G内的概率为 ⚫ P{(X,Y)G}= 在几何上,以G为底, 以曲面z=f(x,y)为顶的柱体体积 4°若f(x,y)在点(x,y)处连续,则有 =f(x,y) − − f (u,v)dudv G f (x, y)dxdy x y F x y ( , ) 2 x O y z z=f(x,y) G 此时的分布函数关于x或y均是连续的

§3.1二维随机变量 面密度的概念:由性质,在xy)的连续点(化y)处 有 。fxy)产 'F(x lim F(x+△x,y+△y)-F(x+△x,y)-F(x,y+△y)+F(x,y) Oxoy △x→0+ △x△y △y→0+ 由分布函数的定义,分子刚好是落在矩形区域的 概率,即 =lim P{x<X≤x+△x,y<Y≤y+△yy △x-0+ △x△y △y→0+ 当△△y很小时, ●P{x<X≤x+△x,y<Y≤y+△yfx)xAy, 即随机点落在长方形(化,x+△x]×y,y叶△y内的概率近似 等于长方体的体积,以上此值表明,概率密度为:兽位 面积上的概率值:面密度
18/102 §3.1 二维随机变量 面密度的概念:由性质,在f(x,y)的连续点(x,y)处 有 ⚫ f(x,y)= = 由分布函数的定义,分子刚好是落在矩形区域的 概率,即 ⚫ = 当ΔxΔy很小时, ⚫ ≈f(x,y)ΔxΔy , ⚫ 即随机点落在长方形(x, x+Δx]×(y, y+Δy]内的概率近似 等于长方体的体积,以上比值表明,概率密度为:单位 面积上的概率值:面密度 x y F x y ( , ) 2 x y F x x y y F x x y F x y y F x y y x + + − + − + + → + → + ( , ) ( , ) ( , ) ( , ) lim 0 0 x y P x X x x y Y y y y x + + → + → + { , } lim 0 0 P{x X x + x, y Y y + y}

§3.1二维随机变量 例 设二维随机变量(X,Y)具有概率密度 x,)o. e2x+",x>0,y>0, 其它. (1)求分布函数F(x,y);(2)求概率PY≤X. )2
19/102 (1) ( , );(2) { }. 0, . 2 , 0, 0, ( , ) ( , ) (2 ) F x y P Y X e x y f x y X Y x y = − + 求分布函数 求概率 其 它 例 设二维随机变量 具有概率密度 §3.1 二维随机变量
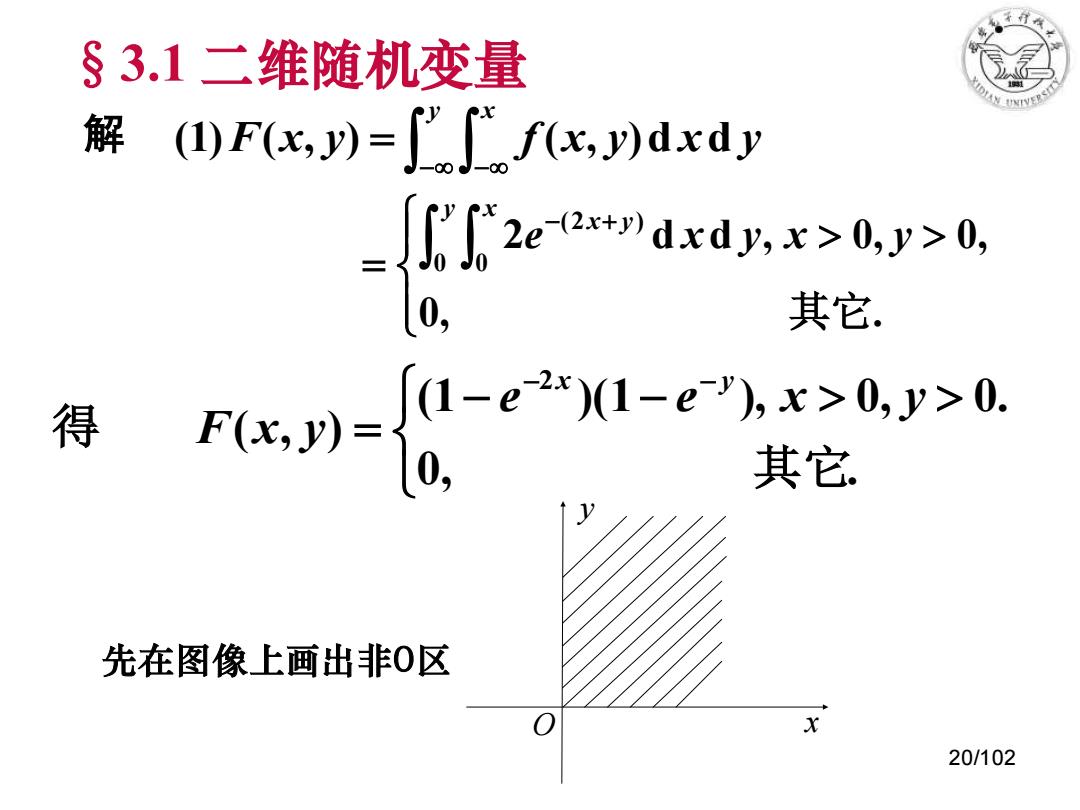
§3.1二维随机变量 (四F(x,)=∫fx,y)dxdy 解 2csdxdy.x>0y0. 0, 其它. 得 n三-eWI-e 其它 先在图像上画出非0区 X 20/102
20/102 解 − − = y x (1)F(x, y) f (x, y)d xd y = − + 0, . 2 d d , 0, 0, 0 0 (2 ) 其它 y x x y e x y x y − − = − − 0, . (1 )(1 ), 0, 0. ( , ) 2 其 它 得 e e x y F x y x y O x y §3.1 二维随机变量 先在图像上画出非0区

§3.1二维随机变量 (2)将(X,Y)看作是平面上随机点的坐标 即有{Y≤X)={(X,Y)∈G}, P{Y≤X}=P{(X,Y)∈G Y-X =∬f(x,)dxdy 2exdxdy ●00 X 3 一般的,涉及到几个随机变量的表达式,在求解概率时就要用几 维分布来求解 /102
21/102 {Y X} = {(X,Y )G}, P{Y X} = P{(X,Y )G} (2) 将 ( X,Y )看作是平面上随机点的坐标 即有 Y = X G x y O f x y x y G ( , )d d = e x y y x y 2 d d 0 (2 ) − + = . 3 1 = §3.1 二维随机变量 一般的,涉及到几个随机变量的表达式,在求解概率时就要用几 维分布来求解