
(4)用MATLAB计算状态反馈向量 用place命令可以计算状态反馈向量ko 以倒摆系统为例,输入以下命令 a=0,1,0,0;0,0,-1,0,0,0,0,1;0,0,11,0:b=0;1;0s-1;p=[-1,-2,-1+i,-1-jl;k=place(a,b,p) 可得到结果 k=-0.4000-1.0000-21.4000-6.0000
⑷ 用MATLAB计算状态反馈向量 用 命令可以计算状态反馈向量 。 place k 以倒摆系统为例,输入以下命令 a=[0,1,0,0;0,0,-1,0;0,0,0,1;0,0,11,0]; b=[0;1;0;-1]; p=[-1,-2,-1+j,-1-j]; k=place(a,b,p) 可得到结果 k = -0.4000 -1.0000 -21.4000 -6.0000

6.4.3多输入系统 如果系统(A,B)是能控的,则通过状态反馈u=r-,K是 pxn常数阵,可以任意配置(A-BK)的特征值。共轭特征值 必须成对配置。 多输入系统极点配置问题是:已知能控的(4,B)和一组期 望特征值(元元,元),求p×n实矩阵K,使(4-BK)的特 征值为(元元.…,)。 多输入系统极,点配置的算法有标准型法和基于求解西尔 维斯特方程的算法。在这一节,标准型法只介绍用龙伯格 能控标准型的算法,而着重介绍基于求解西尔维斯特方程 的算法
6.4.3 多输入系统 如果系统 是能控的,则通过状态反馈 , 是 常数阵,可以任意配置 的特征值。共轭特征值 必须成对配置。 (A,B) u = r-Kx K p× n (A− BK) 多输入系统极点配置问题是:已知能控的 和一组期 望特征值 ,求 实矩阵 ,使 的特 征值为 。 ( , ) λ1, λ 2, L λ n (A,B) p× n ( , ) λ1, λ 2, L λ n K (A− BK) 多输入系统极点配置的算法有标准型法和基于求解西尔 维斯特方程的算法。在这一节,标准型法只介绍用龙伯格 能控标准型的算法,而着重介绍基于求解西尔维斯特方程 的算法

(1)西尔维斯特方程 西尔维斯特方程是具有如下形式的矩阵方程: AT-TF=R (6-50) 式中,A和F可以不是方阵,此时,T和R就不是方阵。若 A和F是nxn方阵,则T和R也是nxn方阵。在状态反馈的计 算中,就属于后者。 西尔维斯特方程求解的问题是:已知A和F,给定R,求 解T。 一般形式的西尔维斯特方程求解是比较困难的,但在A和 F是n×n方阵,且F是对角线型时,西尔维斯特方程就便于 求解了。 下面介绍一种适合于系统综合的西尔维斯特方程(6一50)的 简捷解法
西尔维斯特方程是具有如下形式的矩阵方程: A T −TF = R (6-50) 式中, 和 可以不是方阵,此时, 和 就不是方阵。若 和 是 方阵,则 和 也是 方阵。在状态反馈的计 算中,就属于后者。 A F T R A F n × n n × n 西尔维斯特方程求解的问题是:已知 和 ,给定 ,求 解 。 A F 一般形式的西尔维斯特方程求解是比较困难的,但在 和 是 方阵,且 是对角线型时,西尔维斯特方程就便于 求解了。 下面介绍一种适合于系统综合的西尔维斯特方程 (6—50) 的 简捷解法。 A F n × n F ⑴ 西尔维斯特方程 T R R T

现令T=[42…t」及R=[n乃…)并设 0 0 F= 02 (6—51) 0 0 …0 nJ 则式(6一50)可写成 「 0. 07 0 2 A41t2…tn]-[4t2…tn] =[n r2..m] (6—43) 0 0 0 有 At,-t,2= i=1,2,…,n (6—44) (2I-A0t,=- 说明当E(4(,(4表示A的特征值)时,(1-A)是非奇异的, (,1-A)存在,西尔维斯特方程有唯一解: t=-(2I-A)r (6—45) T=[tht2…tn] (6—46)
现令 及 ,并设 [ ] 1 n T t t t = 2 L [ ] 1 n R r r r = 2 L ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = λ n λ λ 0 0 0 0 0 0 2 1 L M O M L F 则式(6—50)可写成 [ ] 0 0 0 0 0 0 [ ] [ ] 1 2 1 n n A t t t t t t r r r 1 2 n 1 2 n 2 L L M O M L L L = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − λ λ λ (6—43) i n i i i i At − t λ = r = 1 , 2 ,L, i i i (λ I − A)t = − r (6—51) 有 (6—44) (6—46) ( I − A) λi 1 ( ) − λiI − A 说明当 ( 表示 的特征值)时, 是非奇异的, 存在,西尔维斯特方程有唯一解: λ ∉ λ(A) i λ ∉ λ(A) i A i i i t I A r 1 ( ) − = − λ − [ ] n T t t t = 1 2 L (6—45)
若有复极点,例如元=a±B,为避免复数计算,取 [21 0… 0 0 F= 0 0 (6-56) 0 B 0 0 -B 对于复极点有 Ati-ati-Bti= Ati+Bti-a ti+=r (6-57) 写成矩阵形式 4-a] aI-A (6-58) ]f[a] (6-59)
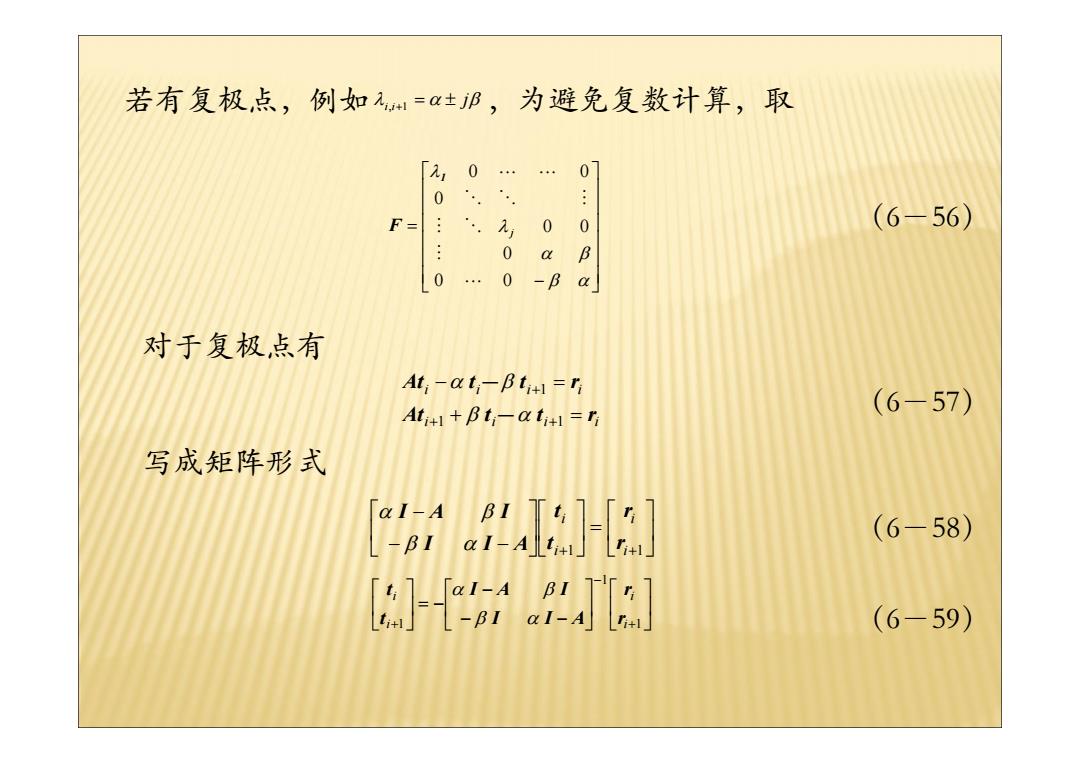
若有复极点,例如 ,为避免复数计算,取 λi,i+1 = α ± jβ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − = β α α β λ λ 0 0 0 0 0 0 0 0 L M M O O O M L L j 1 F 对于复极点有 i i i i i i i i At t t r At t t r + = − = + + + 1 1 1 β α α β - - 写成矩阵形式 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ = ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − +1 i+1 i i i r r t t I I A I A I β α α β ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − ⎥ = − ⎦ ⎤ ⎢ ⎣ ⎡ + − + 1 1 1 i i i i r r I I A I A I t t β α α β (6-56) (6-57) (6-58) (6-59)