
左单位元和右单位元 口e称为系统的左单位元(或左么)当且仅当 HX∈S,ezoX=x 口可以相应地定义系统的右单位元(右么)er a d
𝒆𝑳称为系统的左单位元(或左幺)当且仅当 ∀𝒙 ∈ 𝑺, 𝒆𝑳 ∘ 𝒙 = 𝒙 可以相应地定义系统的右单位元(右幺)𝒆𝑹 * a b c d a a d c a b b d c b c c d c c d d d b d * a b c d a a b c d b a b c d c a b c d d a b c d 16 左单位元和右单位元

关于单位元的进一步讨论 口左、右单位元不一定存在 口左、右单位元不一定唯一 口假设一个代数系统同时有左、右单位元, 则左、右单位元必相等且唯一;即系统 的单位元(幺元) ▣eL=el,oeR=eR 口系统若有单位元,必是唯一的 ▣e1=e1oe2=e2
左、右单位元不一定存在 左、右单位元不一定唯一 假设一个代数系统同时有左、右单位元, 则左、右单位元必相等且唯一;即系统 的单位元(幺元) 𝑒𝐿 = 𝑒𝐿 ∘ 𝑒𝑅 = 𝑒𝑅 系统若有单位元,必是唯一的 𝑒1 = 𝑒1 ∘ 𝑒2 = 𝑒2 17 关于单位元的进一步讨论

逆元(inverse element) 口只对存在单位元的代数系统讨论逆元 口给定系统S中的元素x,若存在S中的元素x',满 足x。x=1s,则称x是x的左逆元;若存在x”, 满足x。x”=1s,则称x"是x的右逆元 给定系统S中的元素x,如果存在S中的元素x*, 满足x。X*=x*。X=15,则称x*是X的逆元, 一般记为x~1 口逆元既是左逆元,又是右逆元 口如果y是x的逆元,则x也是y的逆元
只对存在单位元的代数系统讨论逆元 给定系统𝑆中的元素𝑥,若存在𝑆中的元素𝑥′,满 足𝑥 ′ ∘ 𝑥 = 𝟏𝑺,则称𝑥′是𝑥的左逆元;若存在𝑥′′, 满足𝑥 ∘ 𝑥 ′′ = 𝟏𝑺,则称𝑥′′是𝑥的右逆元 给定系统𝑆中的元素𝑥 ,如果存在𝑆中的元素𝑥 ∗ , 满足𝑥 ∘ 𝑥 ∗ = 𝑥 ∗ ∘ 𝑥 = 𝟏𝑺,则称𝑥 ∗是𝑥的逆元, 一般记为𝒙 −𝟏 逆元既是左逆元,又是右逆元 如果𝑦是𝑥的逆元,则𝑥也是𝑦的逆元 18 逆元(inverse element)
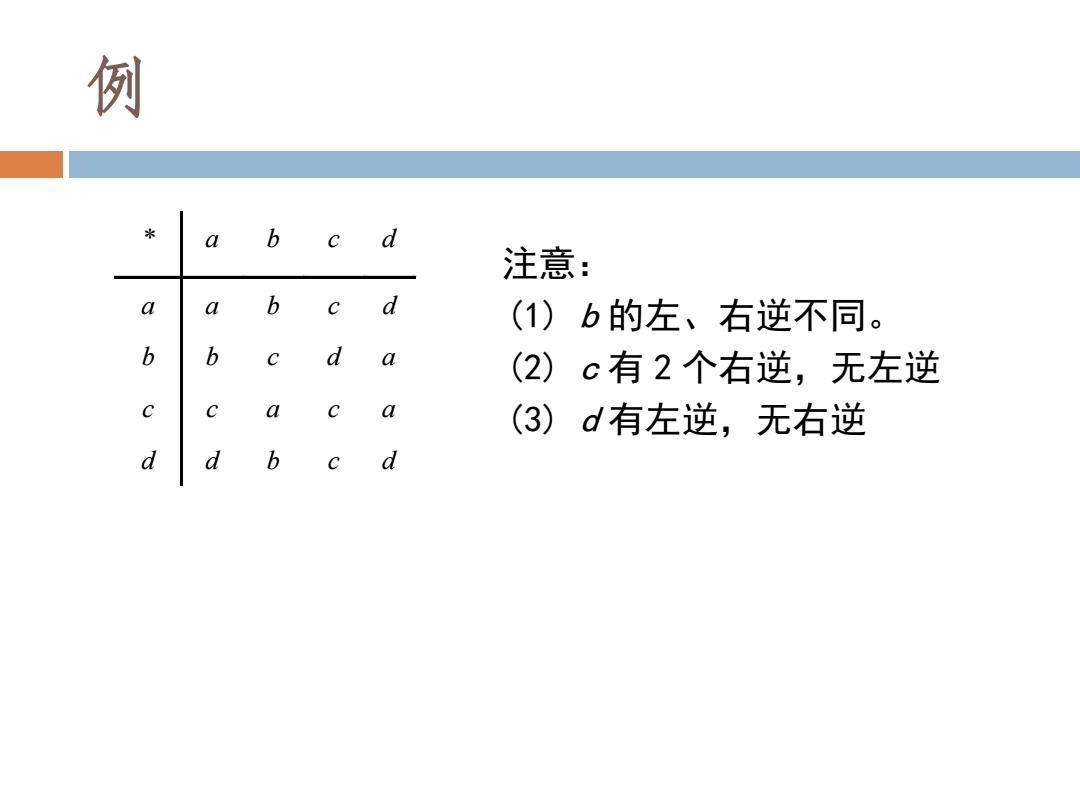
例 b 注意: a a b c d (1)b的左、右逆不同。 b b d a (2)c有2个右逆,无左逆 a a (3)d有左逆,无右逆 d d b d
例 注意: (1) b 的左、右逆不同。 (2) c 有 2 个右逆,无左逆 (3) d 有左逆,无右逆 * a b c d a a b c d b b c d a c c a c a d d b c d 19

关于逆元的进一步讨论 口如果代数系统S,)满足结合律: 口若给定的元素既有左逆,又有右逆,二者必相等且唯一 ■假设x的左逆是x',右逆是x": x'=x'。1s=x'0(x0x")=(x'ox)。x”=1sox"=x" 口若每个元素均有左逆,则左逆即右逆,且逆元唯一 ■任给S中元素a,设a的左逆是b,b的左逆是c,则 aob=(1soa)ob=(cob)。a)ob=(c。(boa)。b= (co1s)ob=C。b=1s
如果代数系统 𝑆, ∘ 满足结合律: 若给定的元素既有左逆,又有右逆,二者必相等且唯一 ◼ 假设𝑥的左逆是𝑥′,右逆是𝑥 ′′: 𝑥 ′ = 𝑥 ′ ∘ 𝟏𝑺 = 𝑥 ′ ∘ 𝑥 ∘ 𝑥 ′′ = 𝑥 ′ ∘ 𝑥 ∘ 𝑥 ′′ = 𝟏𝑺 ∘ 𝑥 ′′ = 𝑥′′ 若每个元素均有左逆,则左逆即右逆,且逆元唯一 ◼ 任给𝑆中元素𝑎,设𝑎的左逆是𝑏,𝑏的左逆是𝑐,则 𝑎 ∘ 𝑏 = 𝟏𝑺 ∘ 𝑎 ∘ 𝑏 = 𝑐 ∘ 𝑏 ∘ 𝑎 ∘ 𝑏 = 𝑐 ∘ 𝑏 ∘ 𝑎 ∘ 𝑏 = 𝑐 ∘ 𝟏𝑺 ∘ 𝑏 = 𝑐 ∘ 𝑏 = 𝟏𝑺 20 关于逆元的进一步讨论