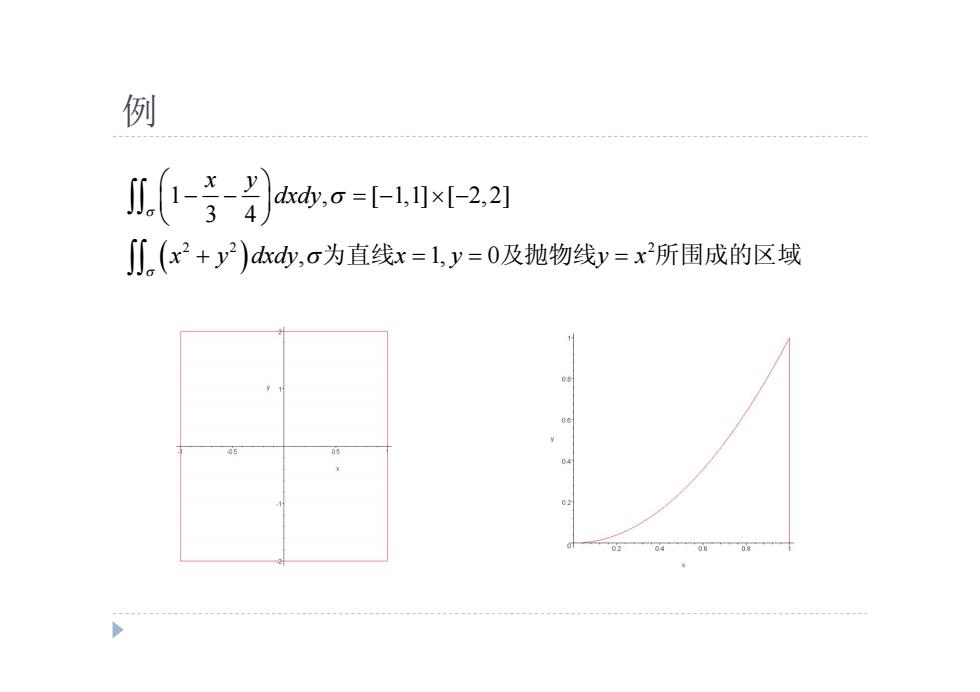
例 .-青-,o=-l小x-22 八(x+y)d,o为直线x=ly=0及抛物线y=x所围成的区域
例 2 2 2 1 , [ 1,1] [ 2,2] 3 4 , 1, 0 x y dxdy x y dxdy x y y x 为直线 及抛物线 所围成的区域

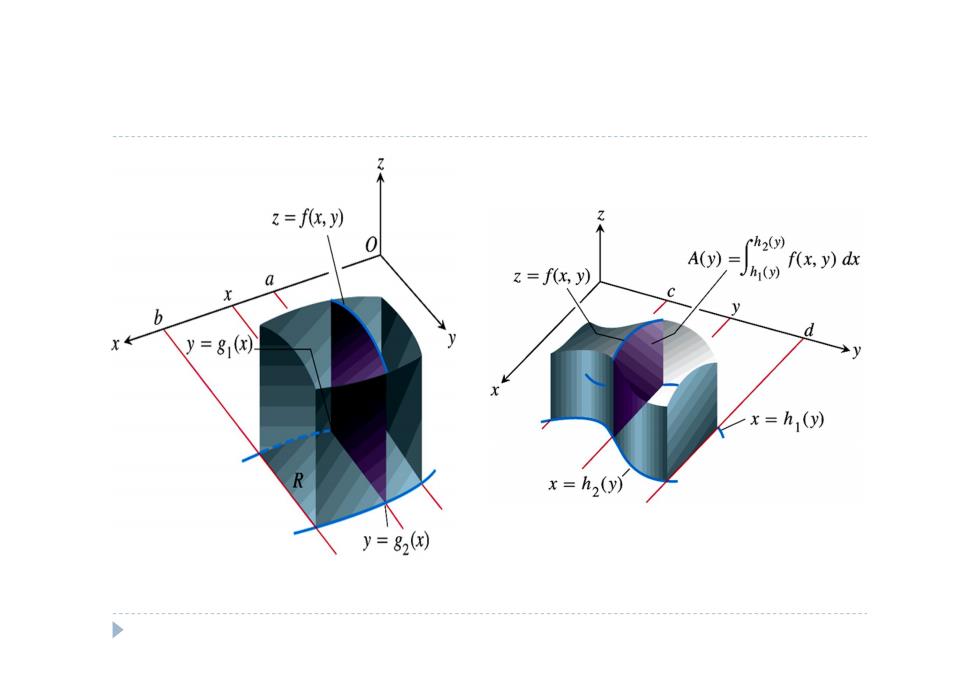
有界集合上二重积分的计算 设点集B={(x,y):y(x)≤(x)≤,(x),a≤x≤b},其中函数y,和y,在 [a,b]上连续,函数f在B上可积,如果对每一x∈[a,b],单变量积分 f(区存在,那么。=f) 类似地,如果点集B={《x,y):x(y)≤x≤x(y),c≤y≤d),其中函数 x和x,在a,b]上连续,函数f在B上可积,如果对每一y∈[a,b],单变 量积分∫fx,k存在,那勾/本=f(c)本
有界集合上二重积分的计算 2 1 2 1 1 2 1 2 ( ) ( ( ) ) ( 1 2 1 2 ) ( , ) : ( ) ( ) ( ), , [ , ] [ , ] , ( , ) : ( ) ( ), , [ ( ) , , ] y x b y y x B x a y x B x y y x y x y x a x b y y a b f B x a b f x y dy f d f x y dy d B x y x y x x y c y d x b B x x a f x x 设点集 其中函数 和 在 上连续,函数 在 上可积,如果对每一 ,单变量积分 存在,那么 类似地,如果点集 其中函数 和 在 上连续,函数 在 上可积,如果对 2 1 2 1 ( ) ( ( ( ) ) ) [ , ] , ( ) , x y x d x y y B c x y y a b f x y dx f d f x y dx dy x x 每一 ,单变 量积分 存在,那么
2=f(x,y) 0 ch2(y) z=f(x,y) A)JAf伍》 b y=81 x=h (y) R x=h2(y) y=82)
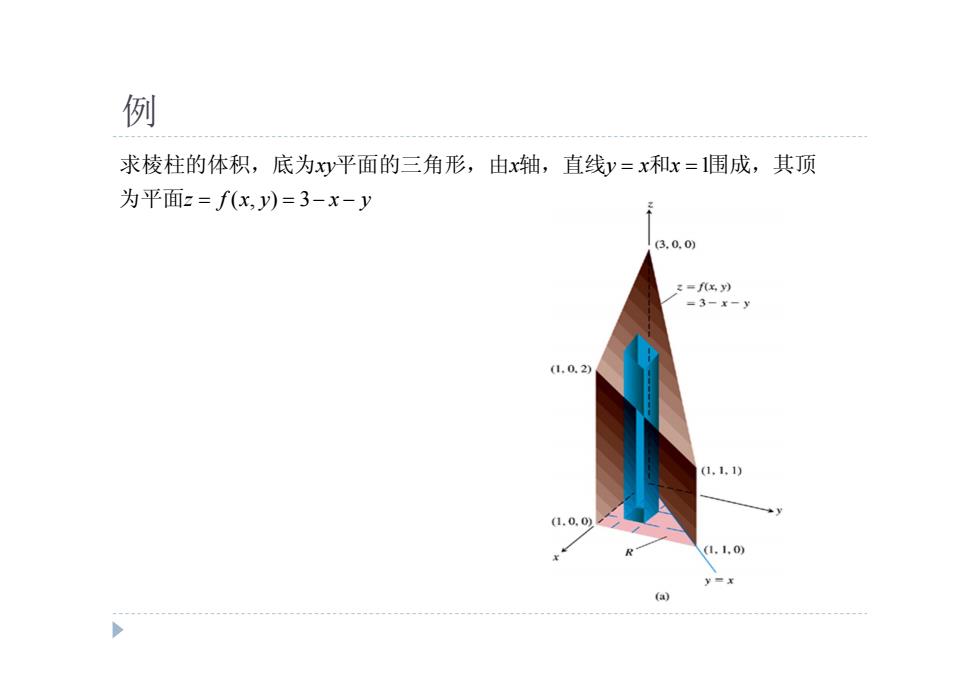
例 求棱柱的体积,底为xy平面的三角形,由x轴,直线y=x和x=1围成,其顶 为平面z=f(x,y)=3-x-y 3.0.0) z=f(x,y) =3-x-y (1.0.2) (1.1,1) (1.0.0 (1.1,0) y=x (a)
例 1 ( , ) 3 xy x y x x z f x y x y 求棱柱的体积,底为 平面的三角形,由 轴,直线 和 围成,其顶 为平面
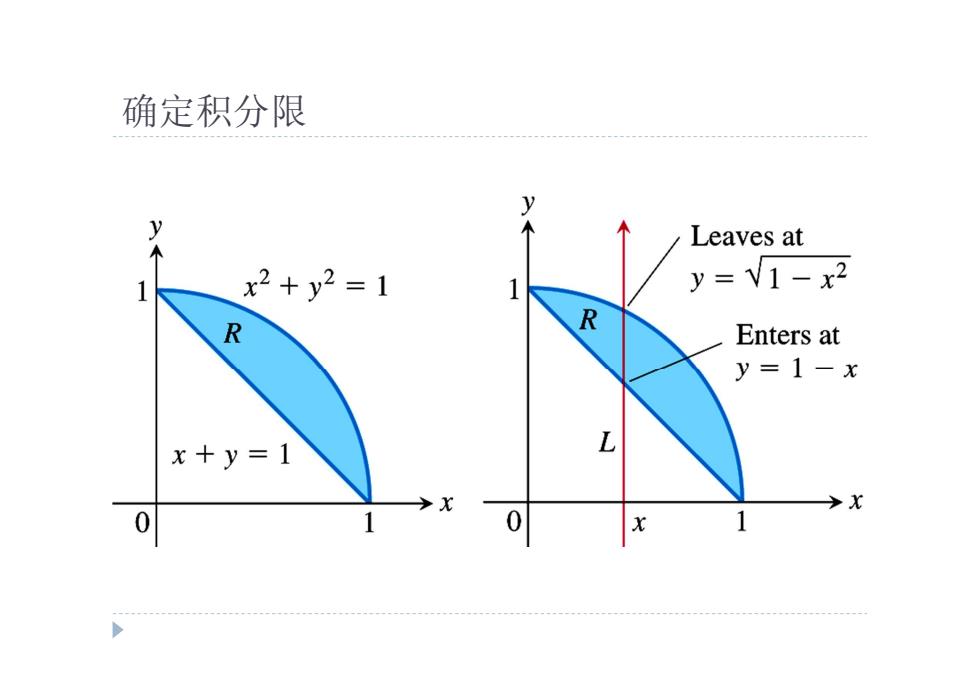
确定积分限 y Leaves at 1 x2+y2=1 1 y=V1-x2 R R Enters at y=1-x x+y=1 L X 0 1
确定积分限