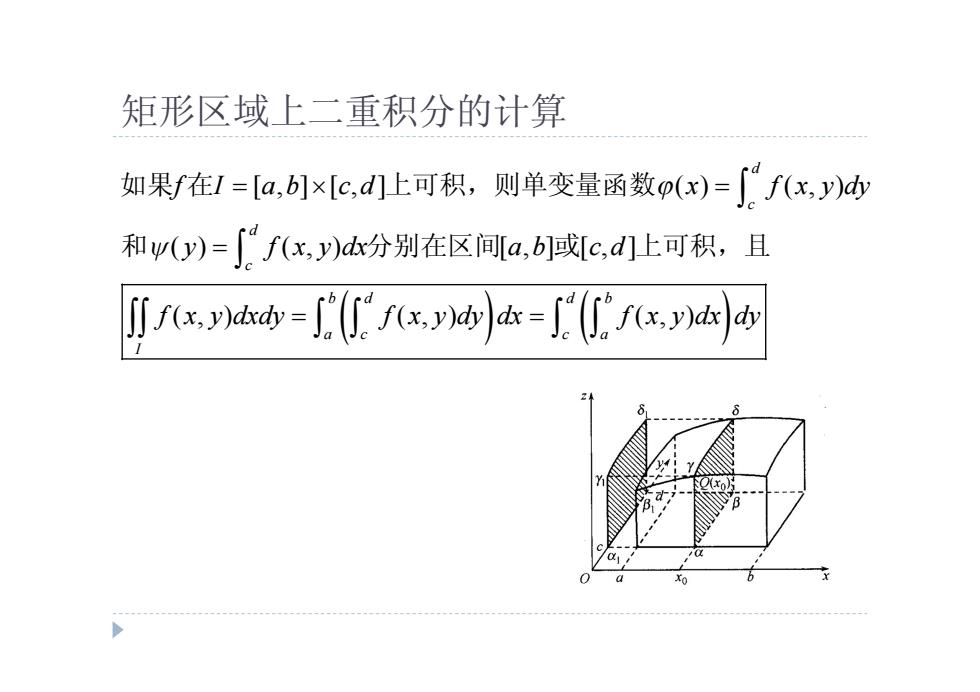
矩形区域上二重积分的计算 如果f在I=[a,b]x[c,d]上可积,则单变量函数p(x)=∫f(x,)山 和yw(y)=∫f(x,y)d分别在区间[a,b]或[c,d上可积,且 ∬fx,dk=(fxy=fx,d
矩形区域上二重积分的计算 [ , ] [ , ] ( ) ( , ) ( ) ( , ) [ , ] [ , ] ( , ) ( , ) ( , ) d c d c b d d b a c c a I f I a b c d x f x y dy y f x y dx a b c d f x y dxdy f x y dy dx f x y dx dy 如果 在 上可积,则单变量函数 和 分别在区间 或 上可积,且
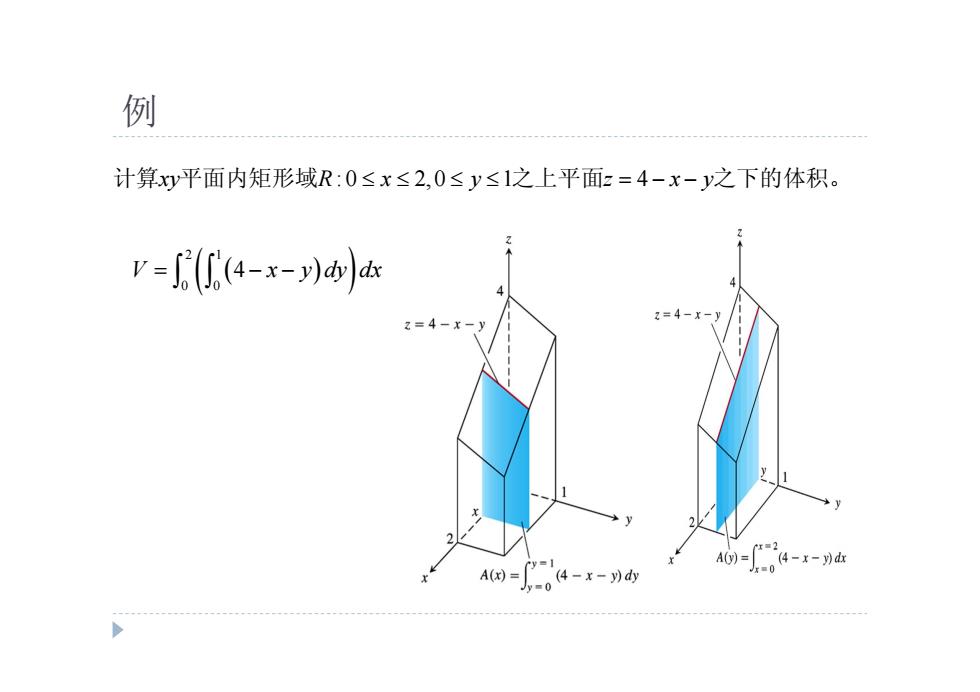
例 计算y平面内矩形域R:0≤x≤2,0≤y≤1之上平面z=4-x-y之下的体积。 r=4-x-列 =4-x A(x)= -04-x-yd西
例 计算xy R x y z x y 平面内矩形域 : 0 2,0 1 4 之上平面 之下的体积。 2 1 0 0 V x y dy dx 4

例 J,ysin(xy)d,I=[0,π]×[0, 0.0 =(ysin()4
例 sin , [0, ] [0,1] I y xy dxdy I 1 0 0 sin 1 y xy dx dy
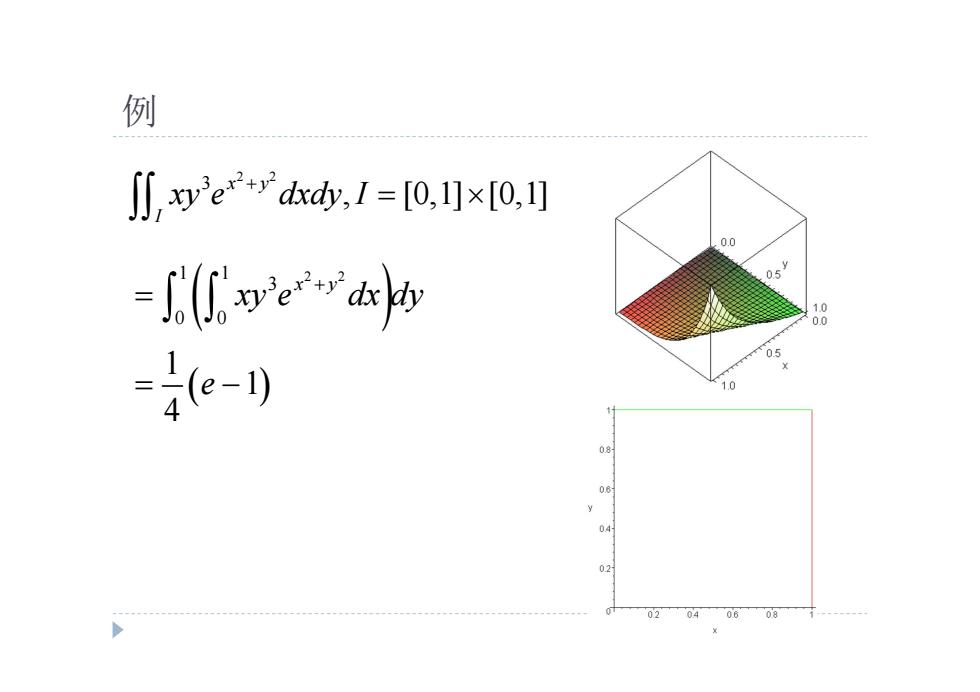
例 J∬,9yerd,1=0,1×f0,1] 0.0 -jyer 05 0.5 =4e-0 0 04 02 09 06 08
例 2 2 3 , [0,1] [0,1] x y I xy e dxdy I 1 1 2 2 3 0 0 1 1 4 x y xy e dx dy e
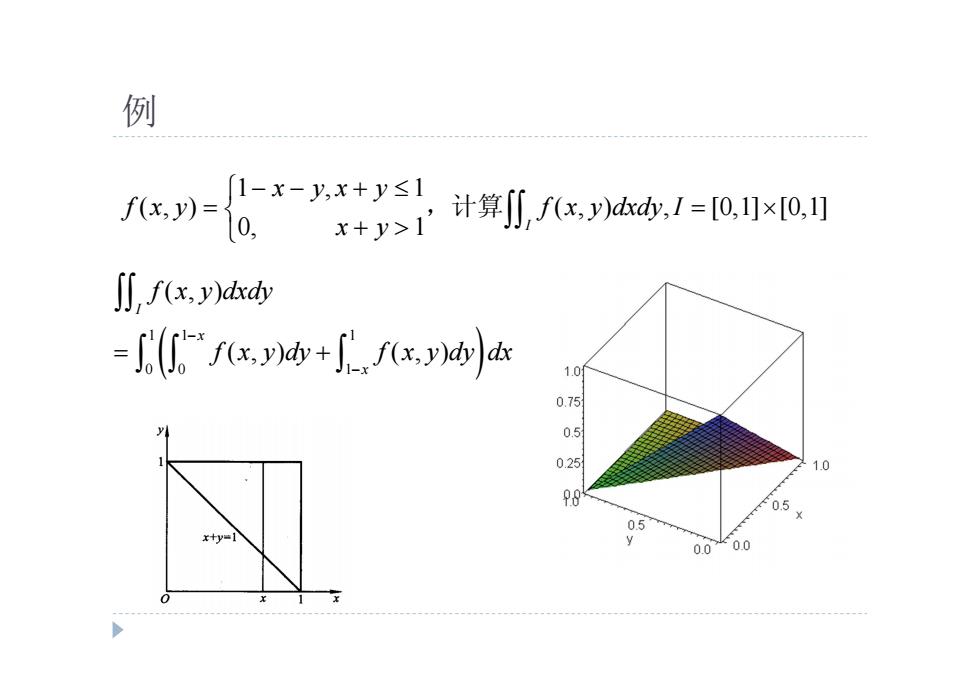
例 f(x,y)= 1-x-y,x+y≤1 0, x+y>1 计算,fx,I=ox0, ∬fx,y)d .ds 10 015 0.5 0.25 10 98 05¥ 05 xty=1 0.0 k0.0
例 1 , 1 ( , ) ( , ) , [0,1] [0,1] 0, 1 I x y x y f x y f x y dxdy I x y ,计算 1 1 1 0 0 1 ( , ) ( , ) ( , ) I x x f x y dxdy f x y dy f x y dy dx