
i j E d×b= a, b 时 b 训b←→ a. by b. 6、混合积 ax [abc]=(i×b)c= 6 b Cs cy c 上页 下页 这回
x y z x y z b b b a a a i j k a b = a b // z z y y x x b a b a b a = = [abc] a b c = ( ) x y z x y z x y z c c c b b b a a a = 6、混合积
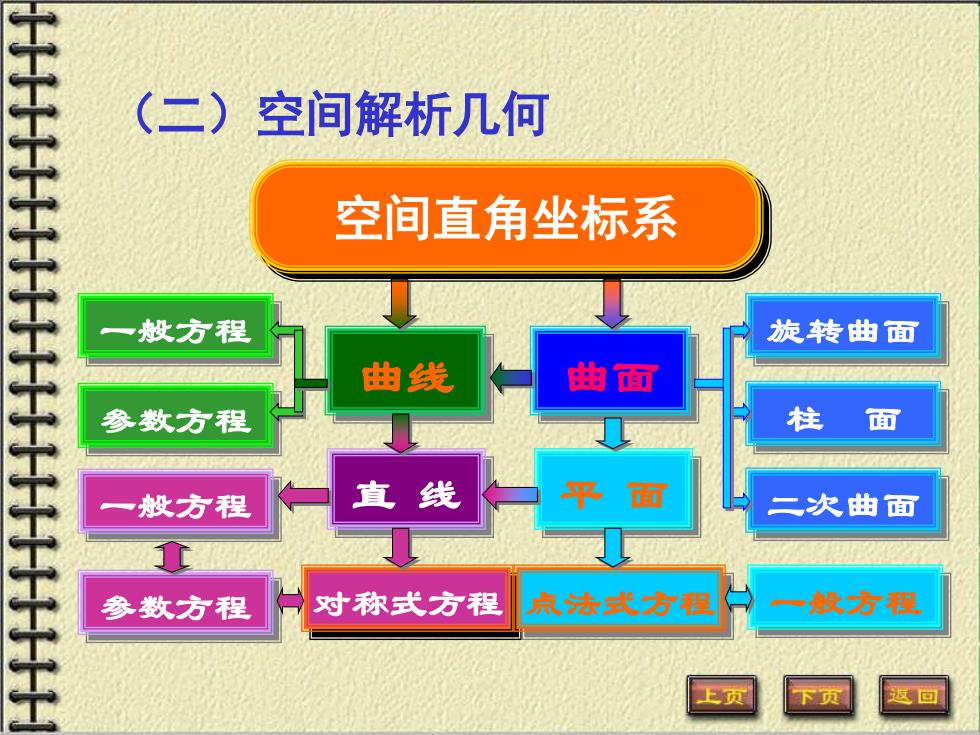
(二)空间解析几何 空间直角坐标系 一般方程 旋转曲面 曲线 曲面 参数方程 柱面 一般方程 直线 平1 面 二次曲面 参数方程 对称式方程 执法武方阻 一批方程 上页 下页 区回
直 线 曲线 曲面 平 面 参数方程 旋转曲面 柱 面 二次曲面 一般方程 参数方程 一般方程 对称式方程 点法式方程 一般方程 空间直角坐标系 (二)空间解析几何
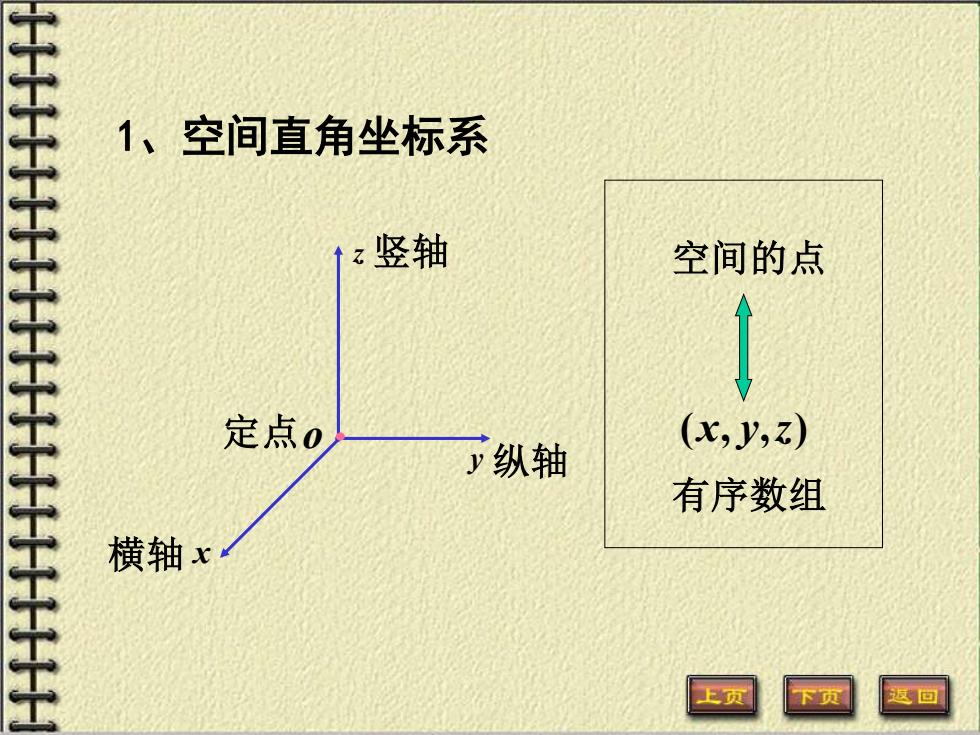
1、 空间直角坐标系 竖轴 空间的点 定点0 少纵轴 (x,v,z) 有序数组 横轴x 上页 下页 区回
横轴 x y 纵轴 z 竖轴 定点 o • 1、空间直角坐标系 空间的点 有序数组 (x, y,z)

空间直角坐标系 共有一个原点,三个坐标轴,三个坐标面,八个卦限 上页 下页 返回
x y o z 空 间 直 角 坐 标 系 共有一个原点,三个坐标轴,三个坐标面,八个卦限

两点间距离公式: 设M1(x1,y1,z1)、M2(x2,Jy2,72)为空间两点 它们距离为 MM2=V(x2-x+(0y2-y)+(a2-z1 上页
( ) ( ) ( ) 2 2 1 2 2 1 2 1 2 2 1 M M = x − x + y − y + z − z 它们距离为 设 ( , , ) 1 1 1 1 M x y z 、 ( , , ) 2 2 2 2 M x y z 为空间两点 两点间距离公式: