
通路的定义(有向图) 6 定义:有向图G中从到v,的长度为n的通路是G的n条 边e,…,en的序列,满足下列性质 口存在∈V,使得1和分别是e的起点和终点(1≤i≤n)。 相关点 口不必区分多重边时,可以用相应顶点的序列表示通路。 口长度为0的通路由单个顶点组成。 口回路:起点与终点相同,长度大于0。 口简单通路:边不重复,即,i,j,j→ee ▣初级通路:点不重复
定义:有向图G中从v0到vn的长度为n的通路是G的n条 边e1 ,…, en的序列,满足下列性质 存在viV, 使得vi-1和vi分别是ei的起点和终点 (1in)。 相关点 不必区分多重边时,可以用相应顶点的序列表示通路。 长度为0的通路由单个顶点组成。 回路:起点与终点相同,长度大于0。 简单通路: 边不重复,即,i, j, ij eiej 初级通路:点不重复 6 通路的定义(有向图)
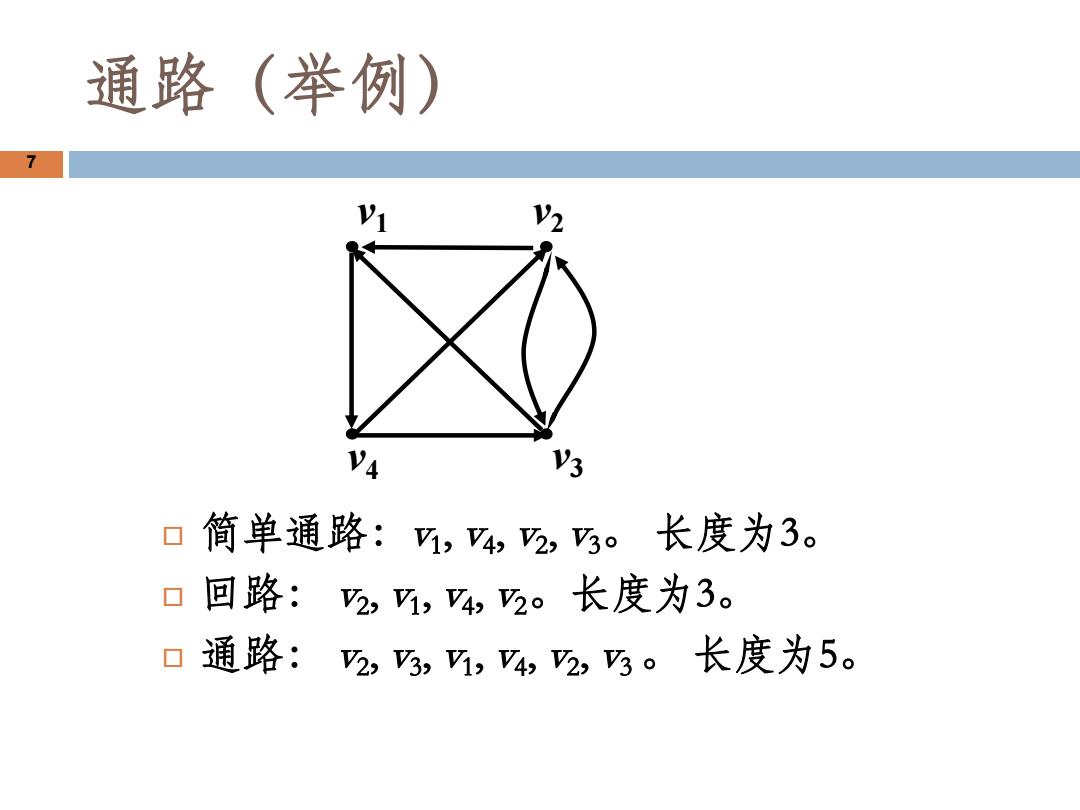
通路(举例) 7 1 V2 V4 V3 口简单通路:,4,2,。长度为3。 口回路:2,1,4,2。长度为3。 口通路:2,,1,4,2,。长度为5
简单通路:v1 , v4 , v2 , v3。 长度为3。 回路: v2 , v1 , v4 , v2。长度为3。 通路: v2 , v3 , v1 , v4 , v2 , v3 。 长度为5。 7 v1 v2 v4 v3 通路(举例)

通路与同构 8 口设图G的邻接矩阵为A ▣(A时:到的长度为k的通路个数 ▣(A:到的长度为的回路个数 口同构图的不变量:长度为的回路的存在性
设图G的邻接矩阵为A (Ak )i,j: vi到vj的长度为k的通路个数 (Ak )i,i: vi到vi的长度为k的回路个数 同构图的不变量:长度为k的回路的存在性。 8 通路与同构
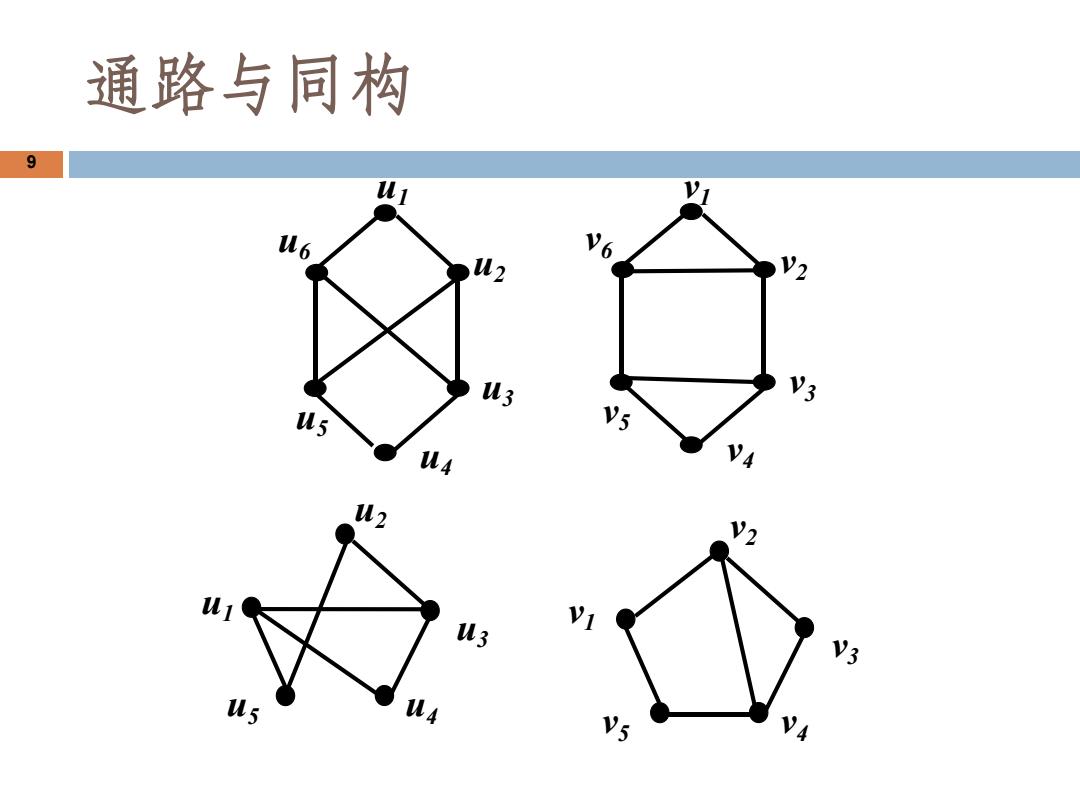
通路与同构 9 ul u6 6 02 V2 u3 v3 us v5 u4 4 u2 V2 u3 Vi v3 us v4
9 u6 u2 u1 u5 u3 u4 v6 v2 v1 v5 v3 v4 u2 u5 u1 u3 u4 v2 v5 v1 v3 v4 通路与同构

本节提要 10 口内容1:通路与回路 口简单通路边不重复、初级通路点不重复 ▣内容2:无向图的连通性 ▣内容3:有向图的连通性
内容1:通路与回路 简单通路边不重复、初级通路点不重复 内容2:无向图的连通性 内容3:有向图的连通性 10 本节提要