
判断以下例子是否是群 (1)<Z,+>,<Q,+>,<R,+>;<Z,+>,<N,+>. (2)<Mn(R),+>,<Mn(R),>. (3)<P(B),⊕>,⊕为对称差运算, (4)<Zm,⊕>,Zn={0,1,n-1},⊕为模n加
(1) <Z,+>,<Q,+>,<R,+>;<Z+ ,+>,<N,+>. (2) <Mn (R),+>,<Mn (R),·>. (3) <P(B),>,为对称差运算. (4) <Zn ,>,Zn={ 0,1, ., n1},为模 n 加. 判断以下例子是否是群
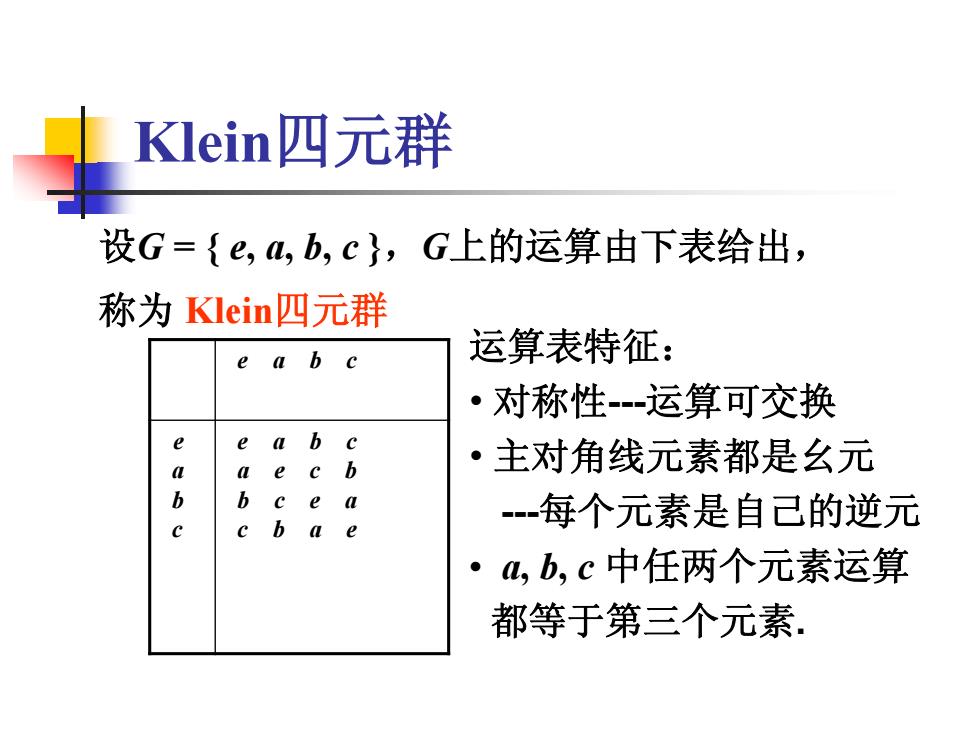
Klein四元群 设G={e,4,b,c},G上的运算由下表给出, 称为Klein四元群 e a b c 运算表特征: ·对称性运算可交换 e a b c e cb ·主对角线元素都是么元 b b c e a c c b -每个元素是自己的逆元 a e ·a,b,c中任两个元素运算 都等于第三个元素
Klein四元群 设G = { e, a, b, c },G上的运算由下表给出, 称为 Klein四元群 e a b c e a b c e a b c a e c b b c e a c b a e 运算表特征: • 对称性-运算可交换 • 主对角线元素都是幺元 -每个元素是自己的逆元 • a, b, c 中任两个元素运算 都等于第三个元素

群的直积 定义群V1=<S1,。>,V2=<S2,*>. 令S=S1×S2并定义S上的·运算如下: V<a,b>,<c,d>ES, <a,b>.<c,d>=<ao c,b*d> 称<S,>为V1和V2的直积,记作V1×V2 可以证明:V1×V2仍群
群的直积 定义 群V1 =< S1, >, V2 =<S2,*>. 令S=S1 S2 并定义S上的 运算如下: <a,b>,<c,d> S, <a,b>·<c,d>= <a c,b*d> 称<S, ·>为V1和V2的直积,记作V1 V2 可以证明:V1 V2仍群

群中的术语 定义1)群G是有穷集,则称G是有限群,否 则称为无限群 群G的基数称为群G的阶 有限群G的阶记作G孔. 2)只含单位元的群称为平凡群 3)若群G中的二元运算是可交换的,则称G 为交换群或阿贝尔(Abel)群
群中的术语 定义 1) 群 G 是有穷集,则称 G 是有限群,否 则称为无限群. 群 G 的基数称为群G的 阶 有限群 G 的阶记作|G|. 2) 只含单位元的群称为平凡群. 3) 若群G中的二元运算是可交换的,则称G 为交换群 或 阿贝尔(Abel)群

实例 <Z,+>和<R,+>是无限群 <Zn,⊕>是有限群,也是n阶群 Klein四元群G={e,a,b,c是4阶群 上述群都是交换群 n阶(≥2)实可逆矩阵集合关于矩阵乘法构成的群 是非交换群
实例 <Z,+> 和 <R,+>是无限群 <Zn ,>是有限群,也是 n 阶群 Klein四元群 G = {e, a, b, c}是 4 阶群 上述群都是交换群 n 阶 (n≥2) 实可逆矩阵集合关于矩阵乘法构成的群 是非交换群