
k k CMCA 高压低压,单分子反应速率的 k3+k.Cu 降变一Lindemann机理特征 关于简单碰撞理论: ☆ 说明了频率因子的概念; A=f(碰撞次数或碰撞频率) ☆适用于气体或液体的简单反应; 单分子,双分子,三分子反应 ☆缺陷:k从实验获得,半经验;对复杂分 子反应,计算值与实验值有相当误差; 引入的校正因子意义不明
高压→低压,单分子反应速率的 3 2 M 降变 —— Lindemann机理特征 1 3 M A k k c k k c c r + = 关于简单碰撞理论: ☆ 说明了频率因子的概念; A = f (碰撞次数或碰撞频率) ☆ 适用于气体或液体的简单反应; 单分子,双分子,三分子反应 ☆ 缺陷: k 从实验获得,半经验;对复杂分 子反应,计算值与实验值有相当误差; 引入的校正因子意义不明
三、对疲状态理论(TST) BE+X→BE.X→B.E.X]t→B.E.X→B+ EX一 u=u(rBE YEX,IBX) u(r) →W=U(BE,r'Ex) 反应势能面图 R BE+X +EX TBE
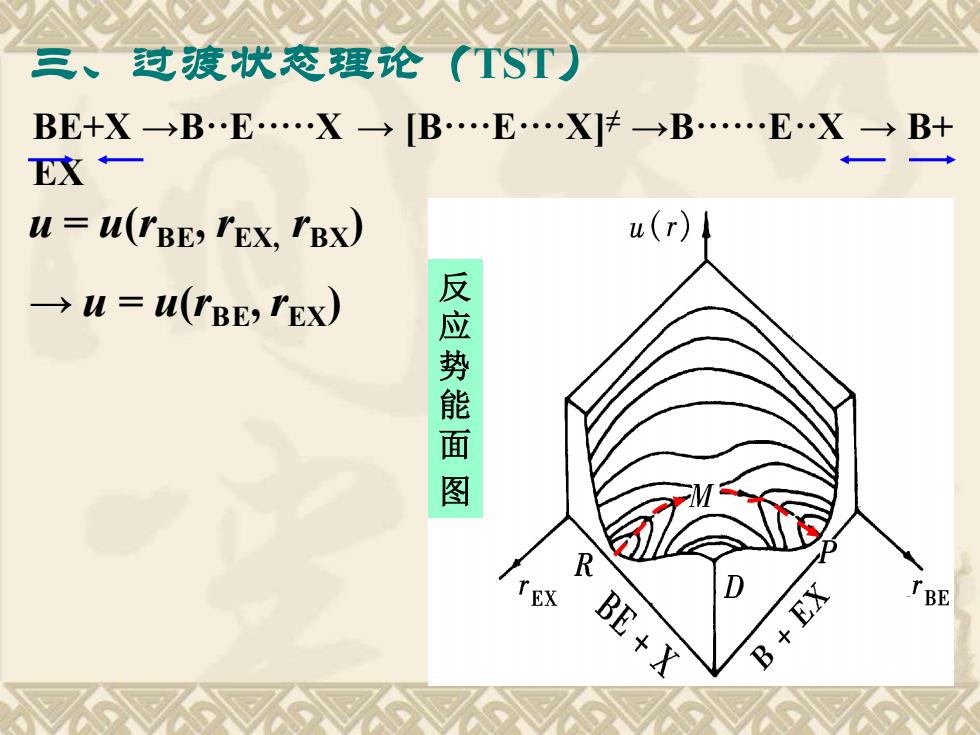
三、过渡状态理论(TST) BE+X →B··E·····X → [B····E····X]≠ →B······E··X → B+ EX u = u(rBE, rEX, rBX) → u = u(rBE, rEX) 反 应 势 能 面 图
R(BE+X) 能量 D(X+B+E) [B.E.X]t BE+X 50 色 B+EX 30 反应进程→ P(B+EX) 反应势能面剖面图 70 TBE 1mol物质反应,活化 反应势能面投影图 能为:E,=L6
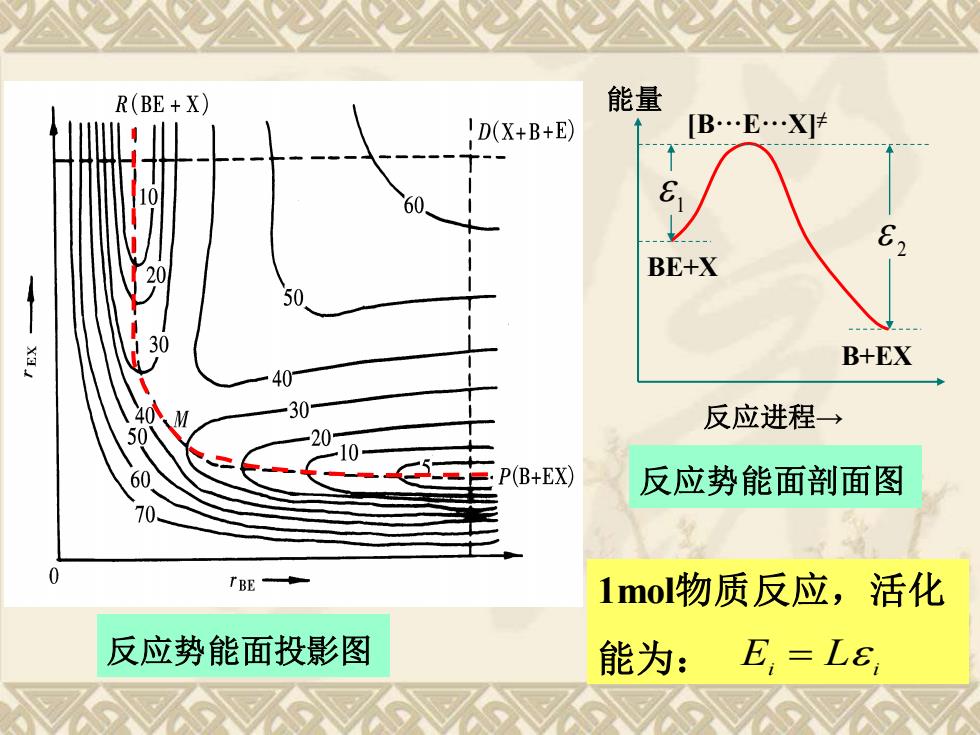
反应势能面投影图 BE+X B+EX 1 2 [B···E···X]≠ 能量 反应进程→ 反应势能面剖面图 1mol物质反应,活化 能为: Ei L i =

反应机理为: ① BE+X÷X :(快) ②[BX]≠→产物 (慢) 导出:E=△H+RT BEXA exp() 的振动频率 A= hL R >A与活化熵变有关,与碰撞理论的结果相 比较得:P与活化熵有关; 若知道过渡状态的构型,就可计算k值。 绝对速率理论
反应机理为: BE+X [BEX]≠ k1 ① k2 (快) ② [BEX]≠→产物 (慢) 导出: E = H +RT a r ◆ A与活化熵变有关,与碰撞理论的结果相 比较得:P与活化熵有关; ◆ 若知道过渡状态的构型,就可计算k值。 ——绝对速率理论 exp( ) e r R S h L R T A = : [BEX]≠ 的振动频率