§9.三元系相图简介 一、三元系相图组成的表示法 水=3-Φ+1=4-,Φmin=1,fmax=3 三维坐标→等边三角立柱 等边三角形—组成三角形 三个立柱侧面一二元相图面 组成三角形的边一二元组成 B 组成三角形的顶点一纯组元
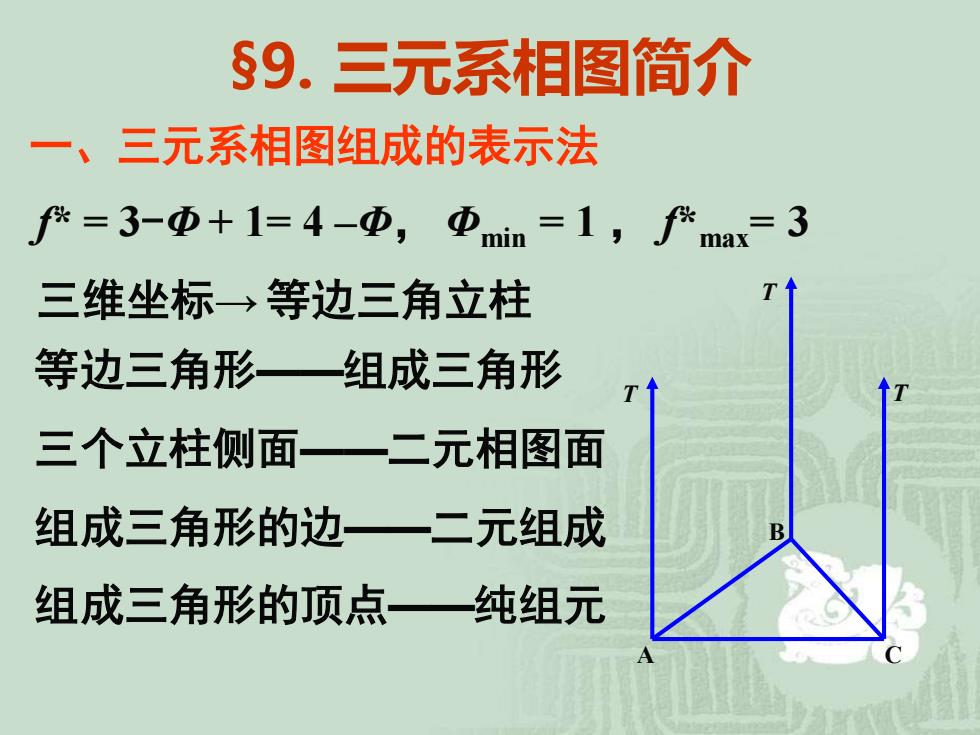
§9. 三元系相图简介 f* = 3-Φ + 1= 4 –Φ, Φmin = 1 , f* max= 3 三维坐标→ 等边三角立柱 A C B T T 等边三角形——组成三角形 T 三个立柱侧面——二元相图面 组成三角形的边——二元组成 组成三角形的顶点——纯组元 一、三元系相图组成的表示法
Cb=Bb'=Pa: 代表体系P中A物的含量; ba'=Cc'=Pb: 代表体系P中B物的含量; Aa'=cb'=Pc: 代表体系P中C物的含量; 1.等含量规则 一组体系点同在平行于三角形某一 边的线上,该则组体系中平行线对 应的顶点组成含量相同
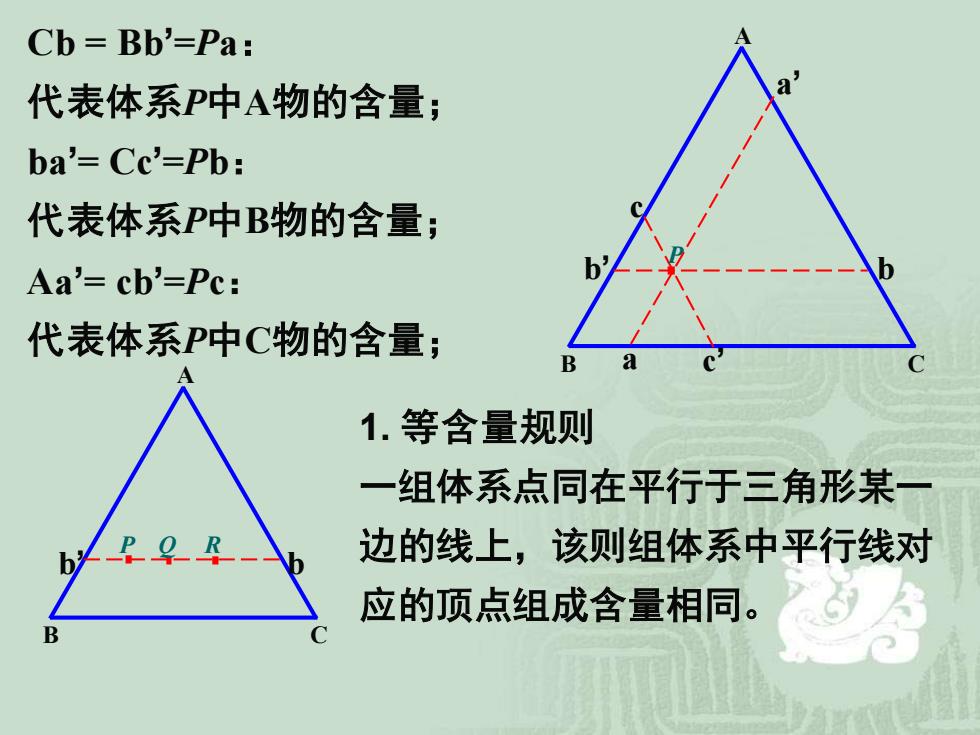
B C A P a a’ b’ b c’ c Cb = Bb’=Pa: 代表体系P中A物的含量; ba’= Cc’=Pb: 代表体系P中B物的含量; Aa’= cb’=Pc: 代表体系P中C物的含量; 1. 等含量规则 一组体系点同在平行于三角形某一 边的线上,该则组体系中平行线对 应的顶点组成含量相同。 B C A b’ b P Q R
2.定比规则 凡位于通过顶点(A)的任一直线上的 R 体系,其中顶点代表的组元含量不 同,其余两组元(B和C)的含量比相 同,即:CB(R=C(P)= CB(O) Cc(R) Cc(P) Ccie 3.杠杆规则 由两个三元体系(M和)混合得到的 新三元体系点(O)一定在M和N的连 线上,且满足杠杆规则: W·MO=W·NO,W。=WM+W
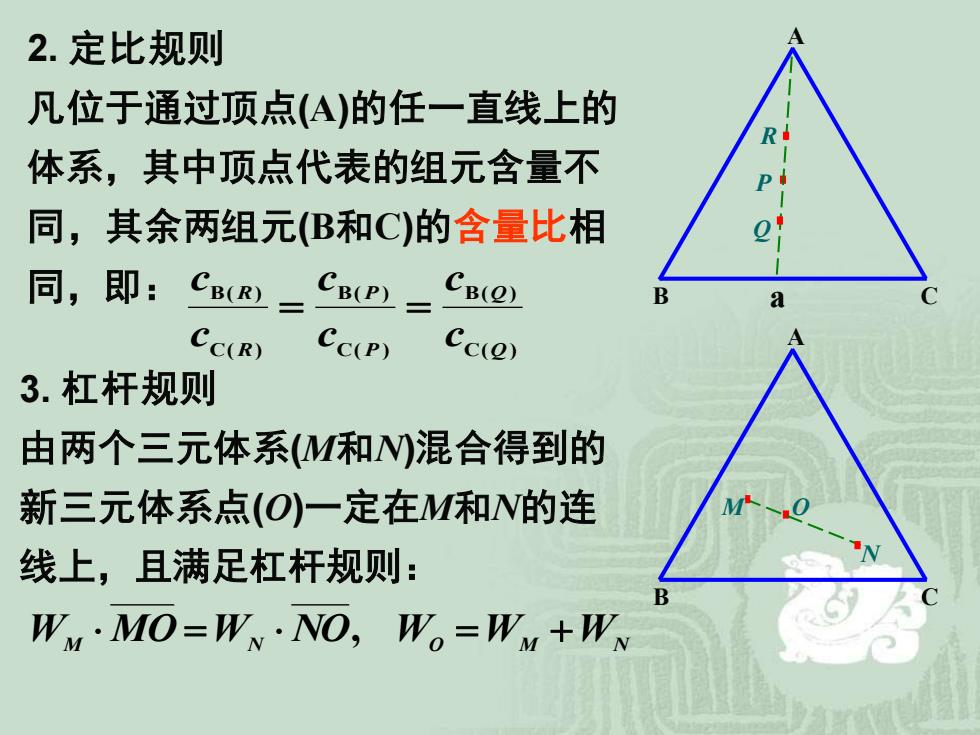
2. 定比规则 凡位于通过顶点(A)的任一直线上的 体系,其中顶点代表的组元含量不 同,其余两组元(B和C)的含量比相 同,即: B C A a P Q R C( ) B( ) C( ) B( ) C( ) B( ) Q Q P P R R c c c c c c = = 3. 杠杆规则 由两个三元体系(M和N)混合得到的 新三元体系点(O)一定在M和N的连 线上,且满足杠杆规则: B C A M O N WM MO WN NO WO =WM +WN =
4.重心规则 由三个三元体系(O、M和N混合得 到的新三元体系点(H)是△MON的 质量重心。 5.背向规则 从一个三元体系中不断取走某一组 元,那么该体系的组成点将沿着原 组成点与代表被取走组元的顶点的 连线向着背离该顶点的方向移动
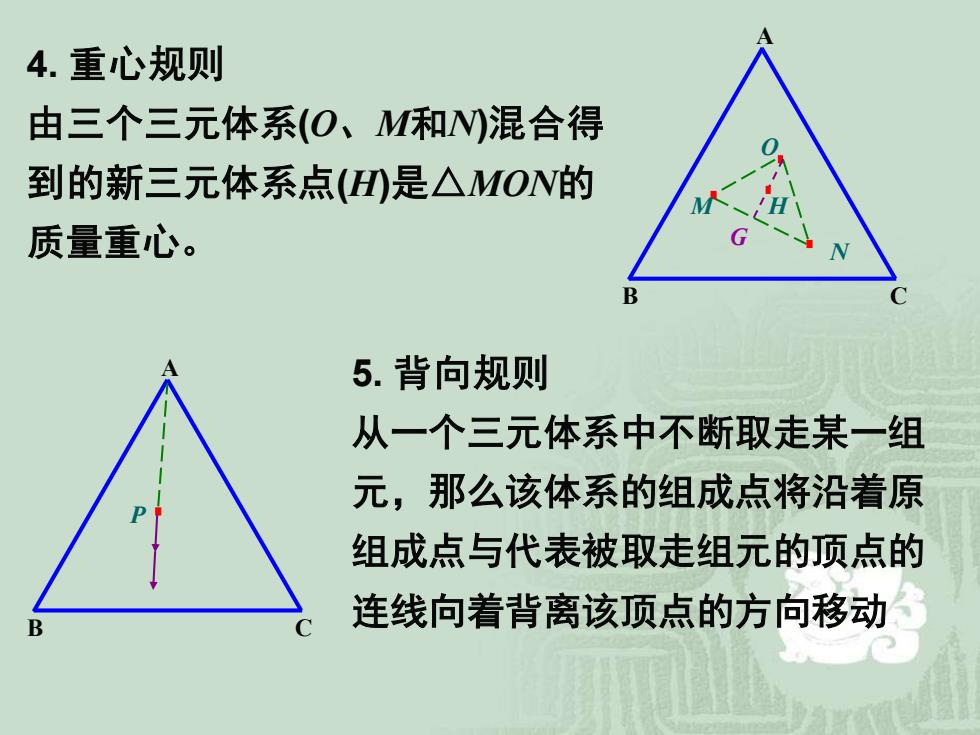
5. 背向规则 从一个三元体系中不断取走某一组 元,那么该体系的组成点将沿着原 组成点与代表被取走组元的顶点的 连线向着背离该顶点的方向移动 4. 重心规则 由三个三元体系(O、M和N)混合得 到的新三元体系点(H)是△MON的 质量重心。 B C A M O N G H B C A P

二、简单共晶三元系 由三个组元两两构成简单二元共晶系组成的 如:Pb-Sn-Bi系 Pb熔点:327℃,Sn熔点:232℃, B熔点:271℃ Wu Pb-Sn共晶温度 182℃,共晶组成 62%Sn (e1) Sn-B共晶温度 139℃,共晶组成 58%Bi (e2) Pb-B共晶温度 128℃,共晶组成 45%Pb (e) Pb-Sn-Bi共晶温度96℃,共晶组成15%Sn,32%Pb(e)
二、简单共晶三元系 由三个组元两两构成简单二元共晶系组成的 如:Pb-Sn-Bi系 Pb熔点: 327℃, Sn熔点: 232℃, Bi熔点: 271℃ Pb-Sn共晶温度 182 ℃, 共晶组成 62%Sn (e1 ) Sn-Bi共晶温度 139 ℃, 共晶组成 58%Bi (e2 ) Pb-Bi共晶温度 128℃, 共晶组成 45%Pb (e3 ) Pb-Sn-Bi共晶温度 96 ℃, 共晶组成 15%Sn, 32% Pb (e) WBi