
第七章表面化学 密切接触的两相之间的过渡区(大约几个分子层厚度)称 为界面,通常有液一气,固一气,固一液,液一液,固一固等界 面。若密切接触的两相中有一相是气体则称为表面。本章讨论 表面(包括界面)现象。 通常的情况下处于系统界面层的分子比物系内部的分子少 得多,因而可以忽略不计。 界面层分子受的力与内部分子受的力不同,因此表现出一 些特殊的性质,当物系的分散度很大时,则必需考虑界面层分 子的特殊性质和由此产生的界面现象
第七章 表面化学 密切接触的两相之间的过渡区(大约几个分子层厚度)称 为界面,通常有液—气,固—气,固—液,液—液,固— 固等界 面。若密切接触的两相中有一相是气体则称为表面。本章讨论 表面(包括界面)现象。 通常的情况下处于系统界面层的分子比物系内部的分子少 得多,因而可以忽略不计。 界面层分子受的力与内部分子受的力不同,因此表现出一 些特殊的性质,当物系的分散度很大时,则必需考虑界面层分 子的特殊性质和由此产生的界面现象

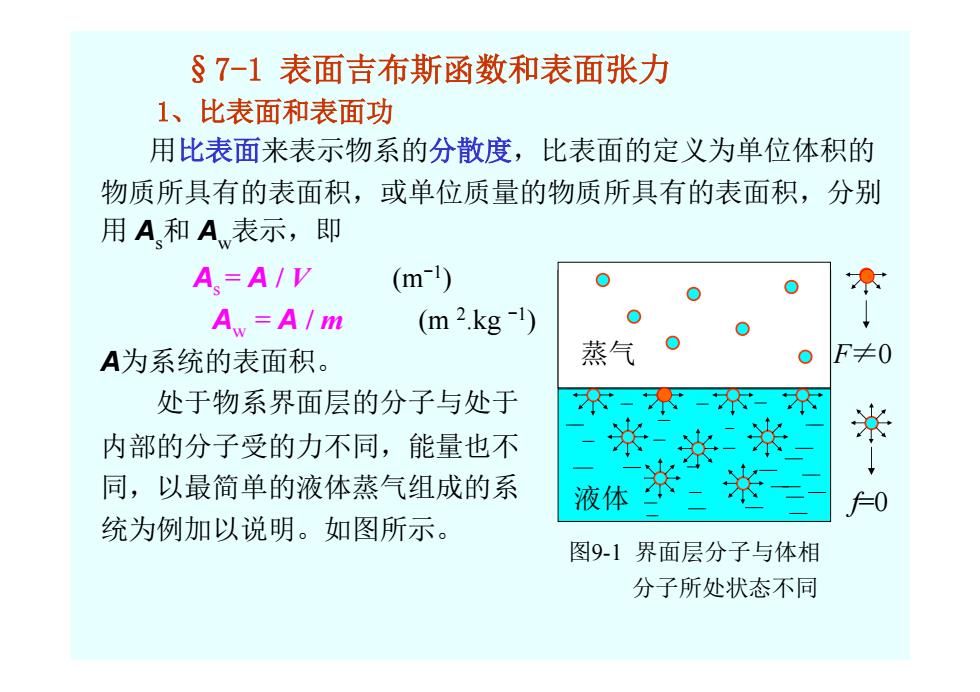
§7-1表面吉布斯函数和表面张力 1、比表面和表面功 用比表面来表示物系的分散度,比表面的定义为单位体积的 物质所具有的表面积,或单位质量的物质所具有的表面积,分别 用A和A表示,即 A.=A/V (m-1) A=A/m (m2.kg-1) A为系统的表面积。 处于物系界面层的分子与处于 内部的分子受的力不同,能量也不 同,以最简单的液体蒸气组成的系 统为例加以说明。如图所示
§7-1 表面吉布斯函数和表面张力 1、比表面和表面功 用比表面来表示物系的分散度,比表面的定义为单位体积的 物质所具有的表面积,或单位质量的物质所具有的表面积,分别 用 As和 Aw表示,即 As = A / V (m-1) Aw = A / m (m 2.kg -1) A为系统的表面积。 处于物系界面层的分子与处于 内部的分子受的力不同,能量也不 同,以最简单的液体蒸气组成的系 统为例加以说明。如图所示
§7-1表面吉布斯函数和表面张力 1、比表面和表面功 用比表面来表示物系的分散度,比表面的定义为单位体积的 物质所具有的表面积,或单位质量的物质所具有的表面积,分别 用A和A表示,即 A.=A/V (m-l) A=A/m (m2.kg1) A为系统的表面积。 蒸气 F≠0 处于物系界面层的分子与处于 内部的分子受的力不同,能量也不 同,以最简单的液体蒸气组成的系 液体 f-0 统为例加以说明。如图所示。 图9-1界面层分子与体相 分子所处状态不同
§7-1 表面吉布斯函数和表面张力 1、比表面和表面功 用比表面来表示物系的分散度,比表面的定义为单位体积的 物质所具有的表面积,或单位质量的物质所具有的表面积,分别 用 As和 Aw表示,即 As = A / V (m-1) Aw = A / m (m 2.kg -1) A为系统的表面积。 处于物系界面层的分子与处于 内部的分子受的力不同,能量也不 同,以最简单的液体蒸气组成的系 统为例加以说明。如图所示。 图9-1 界面层分子与体相 分子所处状态不同 液体 蒸气 F≠0 f=0

其结果导致: ●液体表面有自动收缩的趋势: ·界面层分子有自发与外来分子发生化学或物理结合的趋 势。 由于表面层的分子处于不对称的力场中,使表面层的分子受 到一个向内的拉力,因此要扩大表面积,必须对系统作功。 系统在温度、压力和组成不变的条件下,可逆地增加表面 积时对系统作的非体积功称为表面功,表面功与系统增加的 面积成正比,即 8W'=odA (7-1-1) 式中σ表示在温度、压力和组成不变的条件下,可逆地增加 位表面积对系统作的非体积功,称为比表面功。 8W.=dG=odA 所以o又称为比表面吉布斯函数。单位是Jm2
其结果导致: ●液体表面有自动收缩的趋势; ●界面层分子有自发与外来分子发生化学或物理结合的趋 势。 由于表面层的分子处于不对称的力场中,使表面层的分子受 到一个向内的拉力,因此要扩大表面积,必须对系统作功。 系统在温度、压力和组成不变的条件下,可逆地增加表面 积时对系统作的非体积功称为表面功, 表面功与系统增加的 面积成正比,即 δW '=σdA (7-1-1) 式中 σ 表示在温度、压力和组成不变的条件下,可逆地增加 单 位表面积对系统作的非体积功,称为比表面功。 δWr‘ = dG =σdA 所以σ又称为比表面吉布斯函数。单位是J.m-2

2、表面热力学基本方程 以前在讨论热力学基本方程式时,都假设只有体积功,现在 考虑到表面功时,热力学基本方程式中应增加od4一项。 G=G(T,p.nBs ncs.,A) 式中=(rp 数 称为比表面吉布斯函 dG=-SdT+Vdp+odA +Bupdng 同理: dU=Tds-pdy+odA +BupdnB dH= TdS+dp,+odA+ΣBMpdng dA=-SdT -pdy+odA +BupdnB 上面四个关系式称为热力学基本方程式,由以上关系式可得
2、表面热力学基本方程 以前在讨论热力学基本方程式时,都假设只有体积功,现在 考虑到表面功时,热力学基本方程式中应增加σdA 一项。 G = G (T , p, nB, nC,.,A ) dG = - SdT + Vdp + σdA + ΣB µBdnB 同理: dU = TdS - pdV + σdA + ΣB µBdnB dH = TdS + Vdp + σdA + ΣB µBdnB dA = -SdT - pdV + σdA + ΣB µBdnB 上面四个关系式称为热力学基本方程式,由以上关系式可得 ∑ ∂∂ + ∂∂ + ∂∂ + ∂∂ = ≠ dA AG dn nG dp pG dT TG dG T p n B T p n B p n T n C B , , , , , , ( ) ( ) ( ) ( ) 式中 T p n AG , , ( ) ∂∂ σ = ,称为 比表面吉布斯函 数