
§3.子配分函数的计算 平动子配分函数(P678) 采用量子态分布较方便(不用计算简并度): t 4,=∑e7=∑eBam:) (nx,ny,n2) =.∑.exp (nxny,nz) {+ =qt,x9t,y·9t,z
§3. 子配分函数的计算 一、 平动子配分函数(P678) 采用量子态分布较方便(不用计算简并度): x y z n n n z z y y x x n n n n n n k T q q q l n l n l n m h q e e x y z x y z x y z t, t, t, ( , , ) 2 2 2 2 2 2 2 ( , , ) ( , , ) t 8 exp t t = = + + = = −

三者形式相似:4,cx j=x,y, ni=1 8m 令: 8ml 当a<1时 nx= e=〔)j 2
2 2 2 8 x ml x h 令: = − 三者形式相似: = = 1 2 2 2 t, 8 exp nj j j j l n m h q j = x, y,z 当 1 时 2 x 2 1 2 0 1 2 2 2 t, 2 d 8 exp 2 2 = − = − = h m e n l l n m h q x x n n x x x x x x
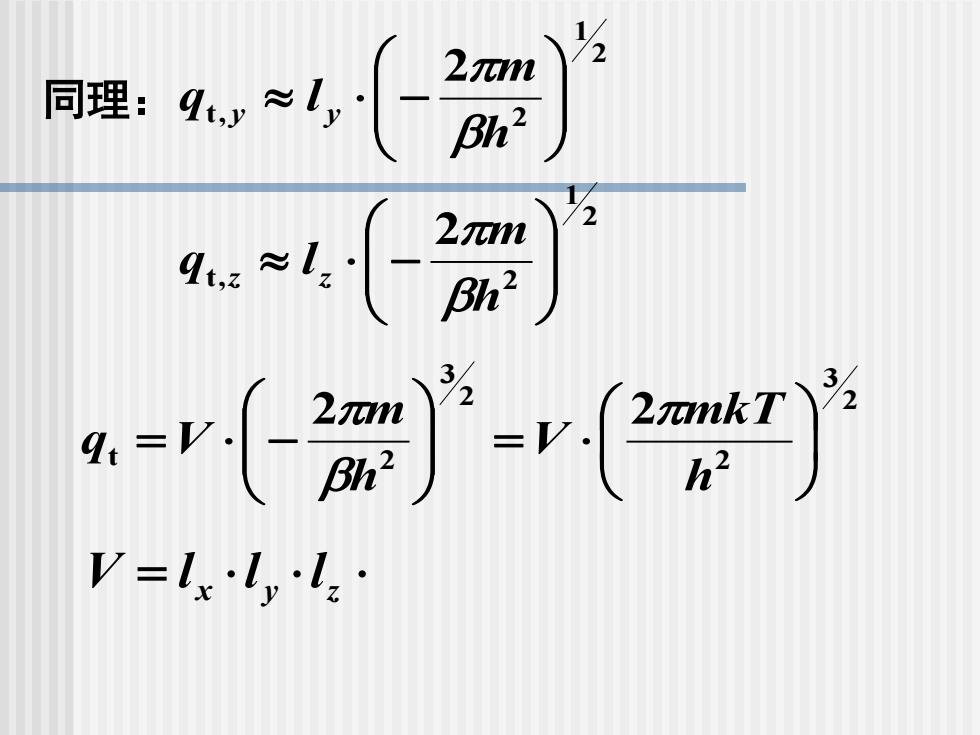
&(-( V=.l
2 1 t, 2 2 − h m q l y y 同理: 2 1 t, 2 2 − h m q l z z 2 3 2 2 3 t 2 2 2 = = − h mkT V h m q V = x y z V l l l

转动子配分函数(P679680) ☆非对称线型分子 J(J+1)h2 J(J+1)⊙ 9.=∑(2J+1)e8xk =∑(2J+1)e ⊙:转动特征温度,表征转动能级间隔的大小 若T>0⊙., 则求和式可化作积分式,得9.=% 若T>⊙,则求和式作级数展开,得 4= ++
二、 转动子配分函数(P679~680) ☆非对称线型分子 + − + − = + = + J T J J Θ J kTI J J h q J e J e r 2 2 ( 1) 8 ( 1) r (2 1) (2 1) Θr :转动特征温度,表征转动能级间隔的大小 若 T Θr ,则求和式可化作积分式,得 r r Θ q = T 若 T Θr ,则求和式作级数展开,得 + + = + + 3 r 2 r r r r 315 4 15 1 3 1 1 T Θ T Θ T Θ Θ T q

若T<<⊙.,则必须严格按求和式计算,即 g=1+3cW2z9)+5c69 ☆对称线型分子 必须考虑对称数(σ≠1) T 如T>⊙.情况下,4= .0 ☆非线型多原子分子(视为三维刚性转子) 对称数σ≠1,在T>>⊙情况下
若 T Θr ,则必须严格按求和式计算,即 = + − + − ) + 6 ) 5exp( 2 1 3exp( r r t T Θ T Θ q ☆对称线型分子 必须考虑对称数(σ≠1) 如 T Θr 情况下, r r Θ T q = ☆非线型多原子分子(视为三维刚性转子) 对称数σ≠1,在 T Θr 情况下