
§4.熵(S)及其应用 一、热功的转换效率与 热力学第二定律的经典表述 1.卡诺循环及可逆热机效率 高温热源(T) (1)恒温可逆膨胀 ,(2)绝热可逆膨胀 锅炉 T1一T2 太空 低温热源(T2) (3)恒温可逆压缩;(4)绝热可逆压缩 T2→T1
§4. 熵(S)及其应用 一、热功的转换效率与 热力学第二定律的经典表述 1. 卡诺循环及可逆热机效率 高温热源(T1) 锅 炉 太 空 低温热源(T2) (1)恒温可逆膨胀;(2)绝热可逆膨胀 T1 T2 (3)恒温可逆压缩;(4)绝热可逆压缩 T2→T1 Q1 Q2
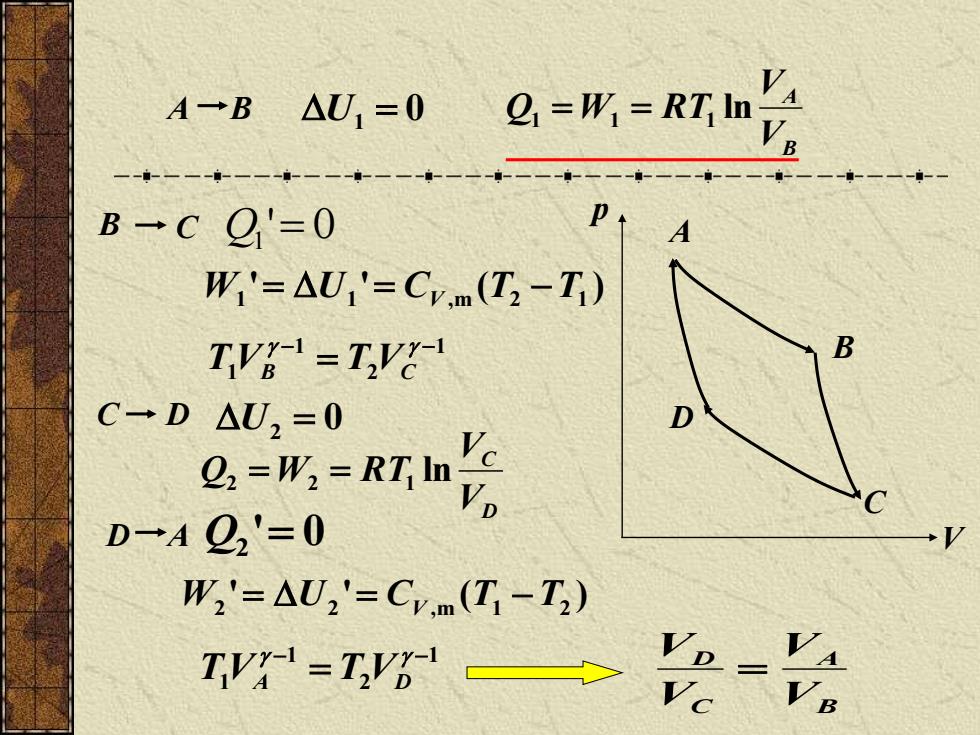
A-B△U,=0 V Q,=用=RT B→cQ'=0 W'=△U1'=C.m(T2-T) TVB-=TVg- C一D△U2=0 D Q.-W:-RTInyp ,'c D-A22'=0 W2'=△U2'=Cm(T-T2)
V p A B C C D B C Q1 ' = 0 ' ' ( ) W1 = U1 = C V , m T2 − T1 D U2 = 0 DC VV Q 2 = W2 = RT1 ln 1 2 1 1 − − = T VB T VC D A Q2 ' = 0 ' ' ( ) W2 = U 2 = C V , m T1 − T2 1 2 1 1 − − = T VA T VD BA CD VV VV = A B U1 = 0 BA VV Q1 = W1 = RT1 ln

e=g,+e.+0+0,=Q,+2,=Rr-In'0 三市 热机效率:7=”_2+2可道1- 21 21 热机 (1)T2不为绝对零度时,7<1。 (2)热功转换具有不可逆性。 功可100%转换成热,热不可能100%转换成功 (3)+9=0
W V V Q Q Q Q Q Q Q R T T B A = − = 1 + 2 + 1 '+ 2 '= 1 + 2 = ( 1 − 2 )ln (1)T2不为绝对零度时, (2)热功转换具有不可逆性。 功可100%转换成热,热不可能100%转换成功 r < 1。 (3) 0 2 2 1 1 + = T Q T Q 1 1 2 1 Q Q Q Q W + = − 热机效率: = 可逆 热机 ——— 1 1 2 T T −T

2.热力学第二定律的经典表述(见教材P208) 实质:自动过程都是不可逆的。 3.卡诺原理 在两个热源之间工作的热机中,可逆热 机效率最大。即:1≥1 ★在两个热源之间工作的一切可逆热机效率 相等。1r=1r ★在两个热源之间工作的可逆热机效率大于 切不可逆热机效率。1.>1r 则: g+g≤0
2. 热力学第二定律的经典表述 (见教材 P208) 实质:自动过程都是不可逆的。 3. 卡诺原理 在两个热源之间工作的热机中,可逆热 机效率最大。即:ηr≥η ★在两个热源之间工作的一切可逆热机效率 相等。ηr = ηr ★在两个热源之间工作的可逆热机效率大于 一切不可逆热机效率。 ηr >ηir 2 2 1 1 T Q T Q 则: + ≤0

二、任意可逆循环过程的热温商与熵函数 热温商:QT 对卡诺循环有:号+ 2=0 p 设任意可逆循环:A一B一A 每个小卡话猫环%% B 整个循环过程:户学,-0或%-0 f9.=9e+9nm=9).a-9)a=0
二、任意可逆循环过程的热温商与熵函数 热温商:Q/T 0 2 2 1 1 + = T Q T Q 对卡诺循环有: 设任意可逆循环:A B A 0 δ δ 1 1 + = + + i i i i T Q T Q 每个小卡诺循环: 整个循环过程: ) 0 δ ( r 1 = i= i i T Q ) 0 δ ( r = i i T Q 或 ) 0 δ ) ( δ ) ( δ ) ( δ ) ( δ ( r = r( ) + r( ) = r( ) − r( ) = B A B A A B B A T Q T Q T Q T Q T Q V p A B