
第五章相平衡热力学 §5-1相变和相变熵 系统中物理性质和化学性质完全相同的部分称为相,物质 从一个相流动到另一个相的过程,称为相变化,简称相变。 相变化(包括气化、冷凝、熔化、凝固、升华、凝华以 及晶型转化等) 1相变焓 通常谈到相变化都是指定温、定压,W=0时的变化过 程, 因此相变过程的热艺是想变榜,即
第五章 相平衡热力学 §5-1 相变和相变熵 系统中物理性质和化学性质完全相同的部分称为 相,物质 从一个相流动到另一个相的过程,称为相变化,简称相变 。 相变化 (包括气化 、冷凝 、熔化 、凝固 、升华 、凝华 以 及晶型转化 等 ) 1 相变焓 通常谈到相变化都是指定温、定压,W‘ =0 时的变化过 程, 因此相变过程的热就是相变焓,即 Q p H β = ∆ α

相变焓:蒸发烙:AvapHm,熔化烙:△usHm,升华焙:△ubHm 晶型转变焓:△rHm 为了计算各种相变过程的热效应,需从化学、化工手册 上查找称为摩尔相变焓的基础实验数据。摩尔相变焓指1mol 纯物质于恒定温度及该温度的平衡压力下发生相变时相应的 焓变,以符号△。BHm(T)表示,单位:kmol。所以, 摩尔蒸发焓ApHm心[Hng-Hm)=A月Hm (5-1-1) 摩尔溶化焓AsHm世Hn)-Hm)=AHm (5-1-2) 摩尔升华焓4 u HH(g)-Hm=AHm (5-1-3) 摩尔转变焓4HmHm(Cr,2)-Hm(Cr,)=AHm (5-1-4) 摩尔冷凝焓为-△aHnm,摩尔结晶焓为-△Hm,摩尔凝华焓 为-△bHm
(5-1-1) 相变焓: 蒸发焓: ∆vapH m,熔化焓: ∆fusH m, 升华焓: ∆subH m, 晶型转变焓: ∆trsH m 为了计算各种相变过程的热效应,需从化学、化工手册 上查找称为摩尔相变焓的基础实验数据。摩尔相变焓指1mol 纯物质于恒定温度及该温度的平衡压力下发生相变时相应的 焓变,以符号ΔαβHm( T )表示,单位:kJ·mol-1。所以, m g m m l def ∆vapHm H (g) − H (l) =∆ H m l m m s def ∆ fusHm H (l) − H (s) =∆ H m g m m s def ∆subHm H (g) − H (s) =∆ H m Cr m m Cr def ∆trsHm H Cr H Cr ∆ H,2,1 ( ,2) − ( ,1) = 摩尔蒸发焓 (5-1-2) (5-1-3) (5-1-4) 摩尔溶化焓 摩尔升华焓 摩尔转变焓 摩尔冷凝焓为-ΔvapHm,摩尔结晶焓为-ΔfusHm,摩尔凝华焓 为-ΔsubHm

在恒温、恒压、非体积功为零的条件下,物质的量为n的某 物质的相变焓可用下式计算 △相变H=n△相变Hm=p (5-1-5) 由于相变过程是在恒压、不作非体积功条件下进行,所以此 相变过程的焓差就等于此过程系统与环境交换的热Q,· 例5-1-1在101.325kPa下,汞的沸点为630K,气化时吸热 291.6 kJ-kg-1,汞气化过程为Hg(1)=Hg(g) 求1.00mol汞在此过程的W、Q、△U及△H。设汞蒸气在此温度 下为理想气体,液体汞的体积可以忽略。(M200.6gmo1) 解:△H=n△aIH=(1.00×291×200.6×103)k=58.5kJ W=-p"g')Fpg-nRT-1.00×8.3145×630kJ=-5.24kJ Q,=△H=58.5kJ △U=2,+W=(58.5-5.24)kJ=53.3kJ
在恒温、恒压、非体积功为零的条件下,物质的量为 n的某 物质 的相变焓可用下式计算 Δ相变H = n Δ相变 Hm = Qp (5-1-5 ) 由于相变过程是在恒压、不作非体积功条件下进行,所以此 相变过程的焓差就等于此过程系统与环境交换的热 Qp 。 例5-1-1 在101.325kPa下,汞的沸点为630K,气化时吸热 291.6kJ·kg-1,汞气化过程为 Hg(1) = Hg(g) 求1.00mol汞在此过程的 W、 Q、Δ U及Δ H。设汞蒸气在此温度 下为理想气体,液体汞的体积可以忽略。( MHg=200.6g·mol-1 ) 解:ΔH = n Δ vapH = (1.00 ×291 ×200.6 ×10-3)kJ = 58.5kJ W= -p ( Vg - V1)= -pVg= -nRT= -1.00 ×8.3145 ×630kJ = -5.24kJ Q p = ΔH = 58.5kJ ΔU = Qp +W = (58.5-5.24)kJ = 53.3kJ

2、相变焓与温度的关系 由于物质的焓是温度与压力的函数,故相变焓应为温度与压力 的函数。但相变焓是指某温度T及该温度对应的平衡压力下物 质发生相变时的焓差,而与温度对应的平衡压力又是温度的函 数,所以摩尔相变焓可归结为温度的函数。一般手册上大多只 列出某个温度、压力下的摩尔相变焓数据,这样,就必须知道 如何由T、p1下的摩尔相变焓数值去求任意温度T,及压力pP2下摩 尔相变焓数值,下面举例说明如何计算。 若有1mol物质B在p1、T,条件下由液相转变为气相,其摩 尔气化焓为△vap Hm(Ti),求在T2p2条件下的△vapHm(T)。求解 状态函数增量问题,必须利用状态函数增量只与始末态有关而 与途径无关的特点,为此可设计如下的过程:
2、相变焓与温度的关系 由于物质的焓是温度与压力的函数,故相变焓应为温度与压力 的函数。但相变焓是指某温度 T 及该温度对应的平衡压力下物 质发生相变时的焓差,而与温度对应的平衡压力又是温度的函 数,所以摩尔相变焓可归结为温度的函数。一般手册上大多只 列出某个温度、压力下的摩尔相变焓数据,这样,就必须知道 如何由T1、p1下的摩尔相变焓数值去求任意温度T2及压力p2下摩 尔相变焓数值,下面举例说明如何计算。 若有1mol物质 B 在 p1、T1 条件下由液相转变为气相,其摩 尔气化焓为ΔvapHm(T1),求在T2、p2条件下的ΔvapHm(T2)。求解 状态函数增量问题,必须利用状态函数增量只与始末态有关而 与途径无关的特点,为此可设计如下的过程:
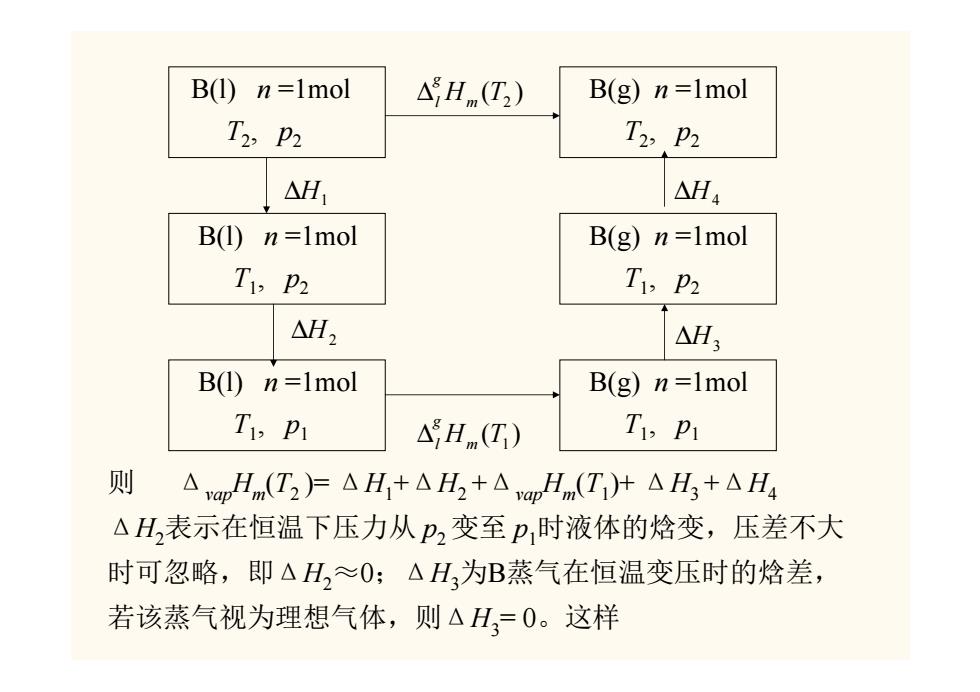
B(1)n=1mol △Hnm(T2) B(g)n=1mol T2,p2 T2,p2 △H1 △H4 B(1)n=1mol B(g)n=1mol T1,p2 T1,p2 △H2 △H3 B(1)n=1mol B(g)n=1mol TP △Hm(T) T p 则 △vapHm(T2)F△H+△H2+△pHm(Ti)+△H3+△H4 △H表示在恒温下压力从p2变至p时液体的焓变,压差不大 时可忽略,即△H,≈O:△H为B蒸气在恒温变压时的焓差, 若该蒸气视为理想气体,则△H,=0。这样
B(l) n =1mol T2, p2 B(l) n =1mol T1, p2 B(l) n =1mol T1, p1 B(g) n =1mol T2, p2 B(g) n =1mol T1, p2 B(g) n =1mol T1, p1 ( ) Hm T2 g ∆l ( ) Hm T1 g ∆l ∆H1 ∆H3 ∆H2 ∆H4 则 ΔvapHm(T2 )= ΔH1+ΔH2 +ΔvapHm(T1)+ ΔH3 +ΔH4 ΔH2表示在恒温下压力从 p2 变至 p1时液体的焓变,压差不大 时可忽略,即ΔH2≈0;ΔH3为B蒸气在恒温变压时的焓差, 若该蒸气视为理想气体,则ΔH3= 0。这样