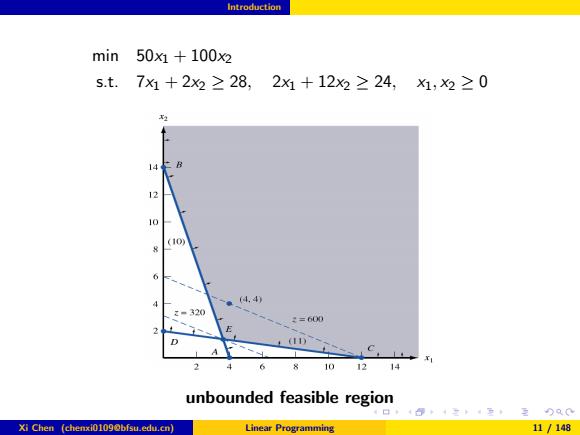
Introduction min 50x1+100x2 s.t. 7X+2x2≥28,2x1+12x9≥24,灯,2≥0 14 B 12 10 (10 4.40 =320 、¥=600 (11) 8 101214 unbounded feasible region Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 11/148
Introduction min 50x1 + 100x2 s.t. 7x1 + 2x2 ≥ 28, 2x1 + 12x2 ≥ 24, x1, x2 ≥ 0 unbounded feasible region Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 11 / 148
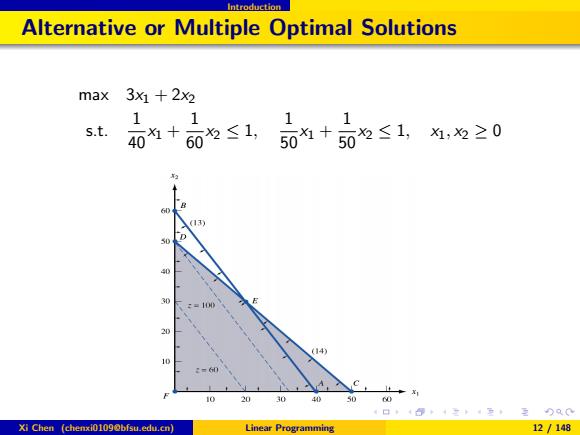
Introduction Alternative or Multiple Optimal Solutions max 3X+2x2 1, s.t. 40 609≤1, 1 1 501+502≤1,,为≥0 60 (13) 30 40 30 20 10 2=60 a 20 40 50 60 Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 12/148
Introduction Alternative or Multiple Optimal Solutions max 3x1 + 2x2 s.t. 1 40 x1 + 1 60 x2 ≤ 1, 1 50 x1 + 1 50 x2 ≤ 1, x1, x2 ≥ 0 Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 12 / 148

Introduction Infeasible LP max 3x1+2x92 11 s.t. 40为+ 609≤1, 501+ 502≤1,为≥30,2≥30 $ 60 (15 50 (17 40 30 20 G (16) 10 20 30 50 60 Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 13/148
Introduction Infeasible LP max 3x1 + 2x2 s.t. 1 40 x1 + 1 60 x2 ≤ 1, 1 50 x1 + 1 50 x2 ≤ 1, x1 ≥ 30, x2 ≥ 30 Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 13 / 148
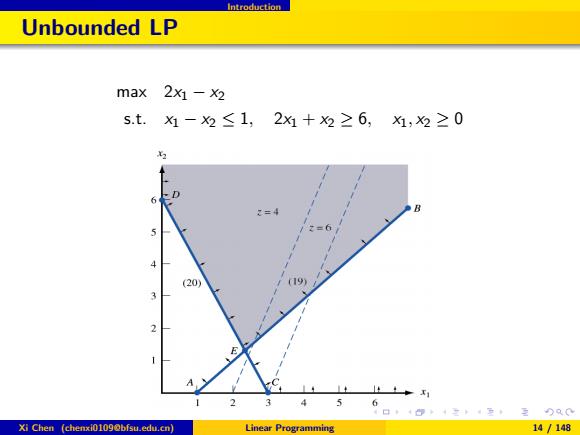
Introduction Unbounded LP max2x灯-2 s.t.x1-为≤1,2x+9≥6,为,2≥0 D (20) 6 Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 14/148
Introduction Unbounded LP max 2x1 − x2 s.t. x1 − x2 ≤ 1, 2x1 + x2 ≥ 6, x1, x2 ≥ 0 Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 14 / 148

Introduction Example 3(A Diet Problem My diet requires that all the food I eat come from one of the four "basic food groups"(chocolate cake,ice cream,soda,and cheesecake).At present,the following four foods are available for consumption:brownies, chocolate ice cream,cola,and pineapple cheesecake.Each brownie costs 50g,each scoop of chocolate ice cream costs 20g,each bottle of cola costs 30g,and each piece of pineapple cheesecake costs 80g.Each day,I must ingest at least 500 calories,6 oz of chocolate,10 oz of sugar,and 8 oz of fat.The nutritional content per unit of each food is shown in the table. How to satisfy my daily nutritional requirements at minimum cost? Nutritional Values for Diet Type of Faod Calaries Sugar (Dunces) Fat (Ounces Brownie 400 2 Chocolate ice cream (I scoop) 200 2 Cola (1 bottle) 150 0 4 Pineapple cheesecake (I piece) 500 0 4 0Q0 Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 15/148
Introduction Example 3 (A Diet Problem) My diet requires that all the food I eat come from one of the four “basic food groups” (chocolate cake, ice cream, soda, and cheesecake). At present, the following four foods are available for consumption: brownies, chocolate ice cream, cola, and pineapple cheesecake. Each brownie costs 50, each scoop of chocolate ice cream costs 20, each bottle of cola costs 30, and each piece of pineapple cheesecake costs 80. Each day, I must ingest at least 500 calories, 6 oz of chocolate, 10 oz of sugar, and 8 oz of fat. The nutritional content per unit of each food is shown in the table. How to satisfy my daily nutritional requirements at minimum cost? Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 15 / 148