
Introduction Assumptions oProportionality:The contribution of the objective function from each decision variable is proportional to the value of the decision variable,and so does each linear constraint. o Additivity:The value of the objective function is the sum of the contributions from individual variables,and so does each linear constraint. oDivisibility:Each decision variable be allowed to assume fractional values.A linear programming problem in which some or all of the variables must be nonnegative integers is called an integer programming problem. o Certainty:Each parameter(objective function coefficient,righthand side,and technological coefficient)is known with certainty. 0Q0 Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 6/148
Introduction Assumptions Proportionality: The contribution of the objective function from each decision variable is proportional to the value of the decision variable, and so does each linear constraint. Additivity: The value of the objective function is the sum of the contributions from individual variables, and so does each linear constraint. Divisibility: Each decision variable be allowed to assume fractional values. A linear programming problem in which some or all of the variables must be nonnegative integers is called an integer programming problem. Certainty: Each parameter (objective function coefficient, righthand side, and technological coefficient) is known with certainty. Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 6 / 148

Introduction Definition 1.2 The feasible region for an LP is the set of all points that satisfies all the LP's constraints and sign restrictions.Any point that is not in an LP's feasible region is said to be an infeasible point. Definition 1.3 For a maximization problem,an optimal solution to an LP is a point in the feasible region with the largest objective function value.Similarly,for a minimization problem,an optimal solution is a point in the feasible region with the smallest objective function value. o Most LPs have only one optimal solution. Some LPs have no optimal solution. o Some LPs have an infinite number of solutions. Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 7/148
Introduction Definition 1.2 The feasible region for an LP is the set of all points that satisfies all the LP’s constraints and sign restrictions. Any point that is not in an LP’s feasible region is said to be an infeasible point. Definition 1.3 For a maximization problem, an optimal solution to an LP is a point in the feasible region with the largest objective function value. Similarly, for a minimization problem, an optimal solution is a point in the feasible region with the smallest objective function value. Most LPs have only one optimal solution. Some LPs have no optimal solution. Some LPs have an infinite number of solutions. Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 7 / 148
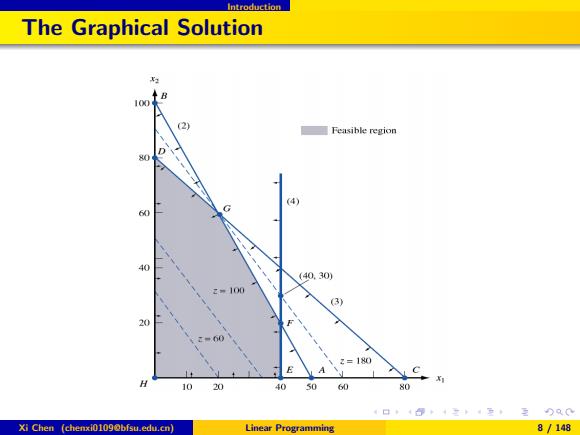
Introduction The Graphical Solution 100 B (2) Feasible region D 80 (4) 60 G 40 (40.30) z=100 (3) 60 2=180 E A C 10 20 40 50 60 80 Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 8/148
Introduction The Graphical Solution Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 8 / 148

Introduction Definition 1.4 A constraint is binding if the left-hand side and the right-hand side of the constraint are equal when the optimal values of the decision variables are substituted into the constraint.If they are unequal with respect to the optimal solutions,a constraint is nonbinding. Definition 1.5 A set of points S is a convex set if the line segment joining any pair of points in S is wholly contained in S.For any convex set S,a point P in S is an extreme point if each line segment that lies completely in S and contains the point P has P as an endpoint of the line segment )Q0 Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 9/148
Introduction Definition 1.4 A constraint is binding if the left-hand side and the right-hand side of the constraint are equal when the optimal values of the decision variables are substituted into the constraint. If they are unequal with respect to the optimal solutions, a constraint is nonbinding. Definition 1.5 A set of points S is a convex set if the line segment joining any pair of points in S is wholly contained in S. For any convex set S, a point P in S is an extreme point if each line segment that lies completely in S and contains the point P has P as an endpoint of the line segment. Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 9 / 148

Introduction Example 2 Dorian Auto manufactures luxury cars and trucks.The company believes that its most likely customers are high-income women and men.To reach these groups,Dorian Auto has embarked on an ambitious TV advertising campaign and has decided to purchase 1-minute commercial spots on two types of programs:comedy shows and football games. Each comedy commercial is seen by 7 million high-income women and 2 million high-income men.Each football commercial is seen by 2 million high-income women and 12 million high-income men.A 1-minute comedy ad costs $50,000,and a 1-minute football ad costs $100,000.Dorian would like the commercials to be seen by at least 28 million high-income women and 24 million high-income men. How Dorian Auto can meet its advertising requirements at minimum cost? 0Q0 Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 10/148
Introduction Example 2 Dorian Auto manufactures luxury cars and trucks. The company believes that its most likely customers are high-income women and men. To reach these groups, Dorian Auto has embarked on an ambitious TV advertising campaign and has decided to purchase 1-minute commercial spots on two types of programs: comedy shows and football games. Each comedy commercial is seen by 7 million high-income women and 2 million high-income men. Each football commercial is seen by 2 million high-income women and 12 million high-income men. A 1-minute comedy ad costs $50, 000, and a 1-minute football ad costs $100, 000. Dorian would like the commercials to be seen by at least 28 million high-income women and 24 million high-income men. How Dorian Auto can meet its advertising requirements at minimum cost? Xi Chen (chenxi0109@bfsu.edu.cn) Linear Programming 10 / 148