
第二节 第十二章 常款项级赵的审敘法 正项级数及其审敛法 二、交错级数及其审敛法 三、绝对收敛与条件收敛 HIGH EDUCATION PRESS 机动目录上页下页返回结束
二、交错级数及其审敛法 三、绝对收敛与条件收敛 第二节 一、正项级数及其审敛法 常数项级数的审敛法 机动 目录 上页 下页 返回 结束 第十二章
正项级数及其审敛法 00 若4n≥0,则称∑4,为正项级数 n= 定理1.正项级数>4n收敛 二部分和序列S n=] (n=1,2,.)有界 证:“一”若∑4n收敛,则{Sn收敛,故有界 n=1 un≥0,∴.部分和数列{Sn}单调递增 又已知{Sn}有界,故{Sn}收敛,从而∑4n也收敛 n= HIGH EDUCATION PRESS 机动目录上页下页返回结束
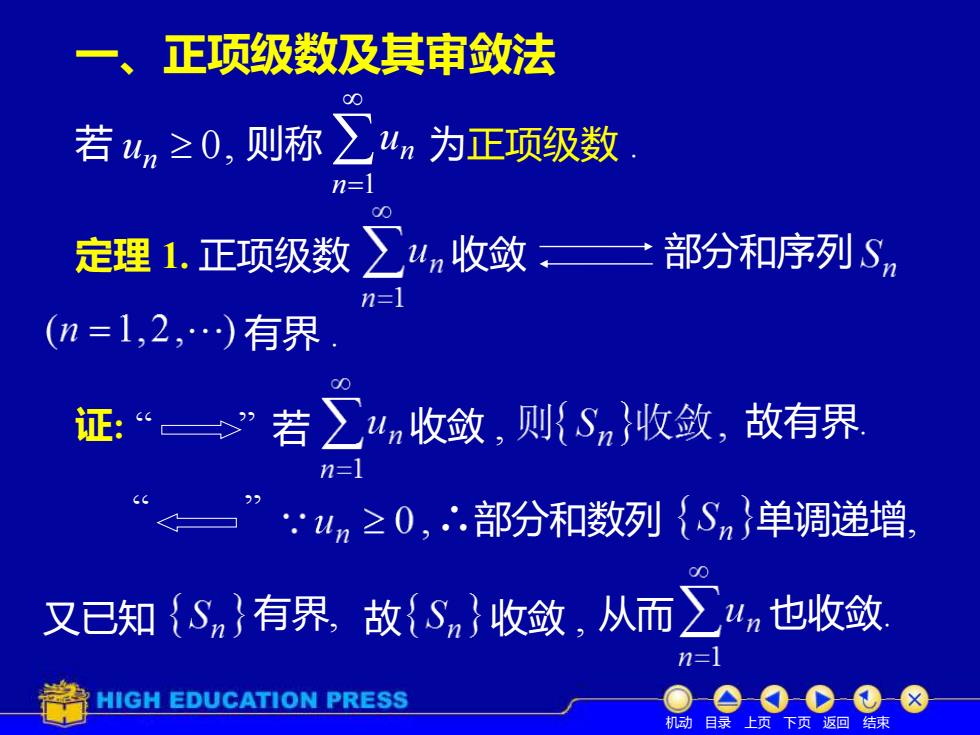
一、正项级数及其审敛法 若 0, un n=1 un 定理 1. 正项级数 收敛 部分和序列 有界 . 若 收敛 , ∴部分和数列 又已知 有界, 故 从而 故有界. 则称 为正项级数 . 单调递增, 收敛 , 也收敛. 证: “ ” “ ” 机动 目录 上页 下页 返回 结束

00 定理2(比较审敛法) 设∑4n,∑yn是两个正项级数 n=1 n=1 且存在N∈Z+,对一切n>N,有un≤kyn(常数k>0), 则有 (①)若强级数∑y收敛,则弱级数∑4,也收敛 n=l n=l 00 (2)若弱级数 ∑4n发散,则强级数∑yn也发散 n=1 n=1 证:因在级数前加、减有限项不改变其敛散性,故不妨 设对一切n∈Z,都有un≤kvn, 令S,和o分别表示弱级数和强级数的部分和,则有 HIGH EDUCATION PRESS Oe0C08 机动目录上页下页返回结束
都有 定理2 (比较审敛法) 设 且存在 对一切 有 (1) 若强级数 则弱级数 (2) 若弱级数 则强级数 证: 设对一切 则有 收敛 , 也收敛 ; 发散 , 也发散 . 分别表示弱级数和强级数的部分和, 则有 是两个正项级数, (常数 k > 0 ), 因在级数前加、减有限项不改变其敛散性, 故不妨 机动 目录 上页 下页 返回 结束

Sn≤kom 00 (1)若强级数∑yn收敛,则有o=1imom n-→0 n=1 因此对一切n∈Z,有Sn≤ko 由定理1可知,弱级数>,也收敛 n=] (2)若弱级数∑4n发散则有1imSn=∞, n=1 1n→00 因此lim n=o∞,这说明强级数 n-→c0 ∑vn也发散 n=】 HIGH EDUCATION PRESS 机动目录上 下页返回结
(1) 若强级数 则有 因此对一切 有 由定理 1 可知, (2) 若弱级数 则有 因此 这说明强级数 也发散 . 也收敛 . 发散, 收敛, 弱级数 机动 目录 上页 下页 返回 结束

例1.讨论p级数1+ +++.(常数p>0 的敛散性 解:1)若p≤l,因为对一切n∈Z, 而调和级数∑,发散,由比较审敛法可知刀级数∑ n=1h 发散 HIGH EDUCATION PRESS 机动目录上页下页返回结束
例1. 讨论 p 级数 + p + p ++ p + n 1 3 1 2 1 1 (常数 p > 0) 的敛散性. 解: 1) 若 p 1, 因为对一切 而调和级数 =1 1 n n 由比较审敛法可知 p 级数 n 1 发散 . 发散 , 机动 目录 上页 下页 返回 结束