
第6章振动力学基础 §6.1简谐振动动力学 §6.2简谐振动运动学 §6.3微振动的简谐近似 §6.4平行简谐振动的合成振动频谱 §6.5垂直简谐振动的合成 §6.6阻尼振动 §6.7受迫振动共振
第 6 章 振动力学基础 §6.1 简谐振动动力学 §6.2 简谐振动运动学 §6.3 微振动的简谐近似 §6.5 垂直简谐振动的合成 §6.4 平行简谐振动的合成 振动频谱 §6.6 阻尼振动 §6.7 受迫振动 共振
§6.4平行简谐振动的合成 振动频谱 、 同频率平行简谐振动的合成 某一质点在直线上同时参与两个独立的同频率的简 谐振动,其振动方程分别表示为: x1=Ac0S(0t+01) x2=A2C0s(0t+p2) 4=4+4 0 x=X+X2
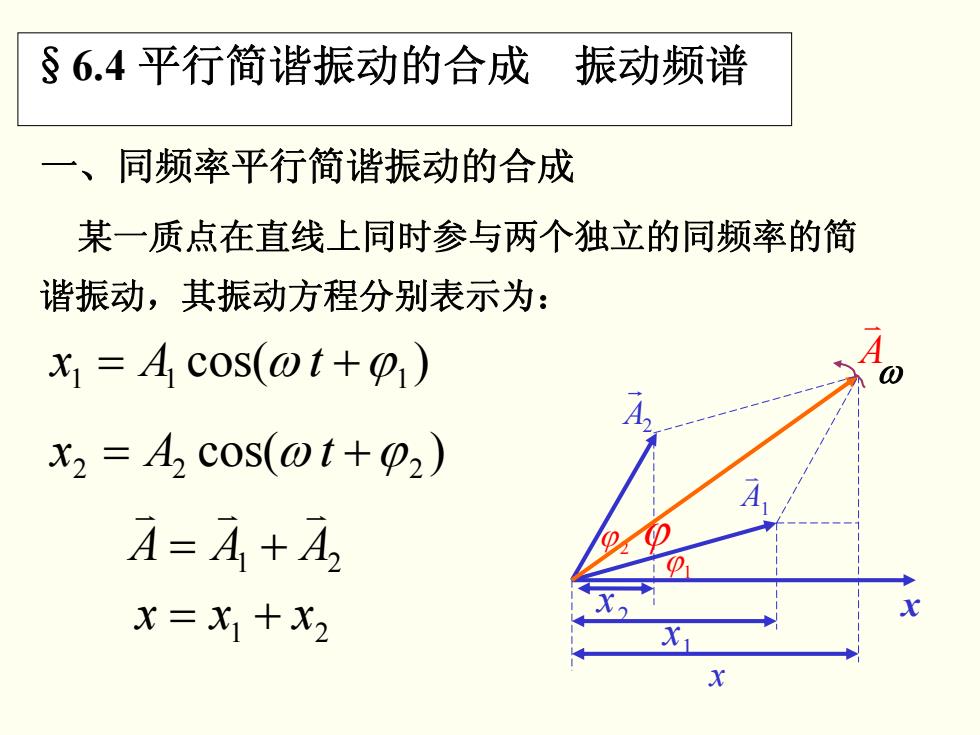
一、同频率平行简谐振动的合成 某一质点在直线上同时参与两个独立的同频率的简 谐振动,其振动方程分别表示为: )cos( = 11 ω + ϕ1 tAx ω x 1 x 2 x cos( ) = 22 ω + ϕ 2 tAx x A1 v A 2 r ϕ1 ϕ 2 A v ϕ AAA 21 v v v += 21 = + xxx §6.4 平行简谐振动的合成 振动频谱

>结论:一个质点参与两个在同一直线上频率相同的简谐振 动,其合成运动仍为简谐振动。 A=VA2+42+2A4c0s(020) A sin o+sinp2 Φ=arctan A cosp+4 cosp2 (1若:02-9,=2km(k=0,±1,±2,) 则:A=VA?+A好+2AA2=A+A (2若:p2-9,=(2k+1)元(k=0,±1,±2,…) 则:A=VA+A-2AA,2=4-A2
一个质点参与两个在同一直线上频率相同的简谐振 动,其合成运动仍为简谐振动 。 ¾结论: cos(2 ) 21 12 2 2 2 1 ++= AAAAA −ϕϕ 1 21 2 211 2 cos cos sin sin arctan ϕ ϕ ϕ ϕ ϕ AA AA + + = 2 π ( ,2,1,0 L ) (1)若: ϕ − ϕ12 = kk = ± ± )12( π ( ,2,1,0 L ) (2)若: ϕ − ϕ12 = + kk = ± ± 2121 2 2 2 则: 1 2 +=++= AAAAAAA 2121 2 2 2 1 则: 2 −=−+= AAAAAAA
[例题6-6]两个同方向的简谐振动曲线(如图所示) 1.求合振动的振幅。 2.求合振动的振动式。 A x2(t) 解:A=A2-A 2π A 0= x,(t) T 元 兀 A1c0s01=0 A 2 2 4,cos0,=02,=± A 2
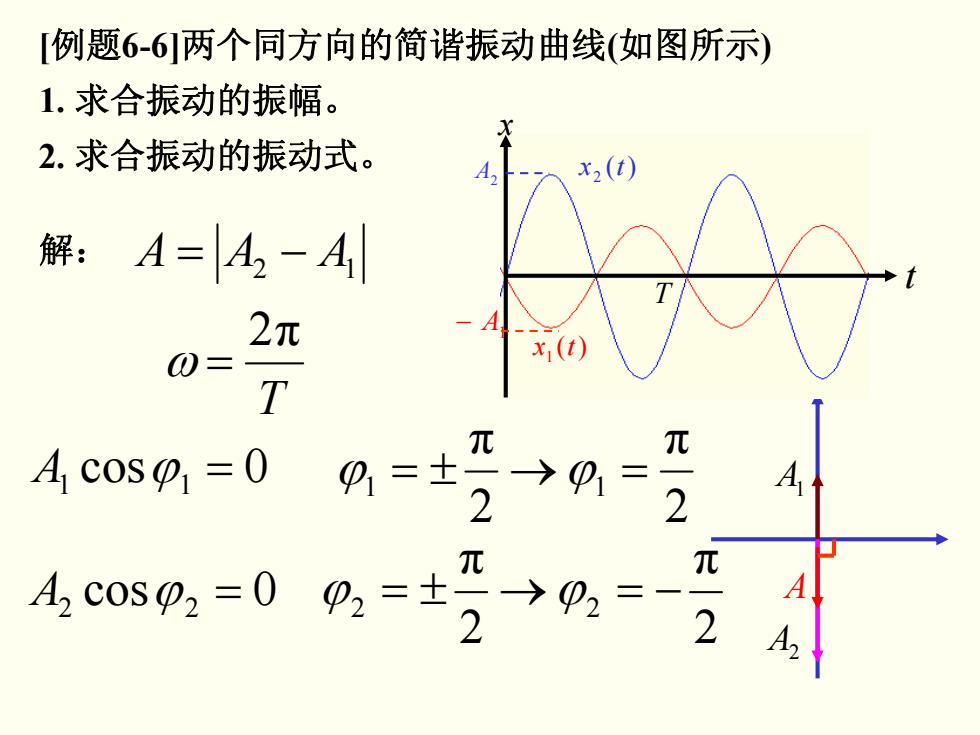
[例题6-6]两个同方向的简谐振动曲线(如图所示) 1. 求合振动的振幅。 2. 求合振动的振动式。 解: −= AAA 12 T 2π ω = 0cos A ϕ11 = 2π 2π ϕ1 ϕ1 =→±= 0cos A ϕ 22 = 2π 2π ϕ2 ϕ2 −=→±= A1 A2 A − A1 A2 x )( 1 tx )( 2 tx T t
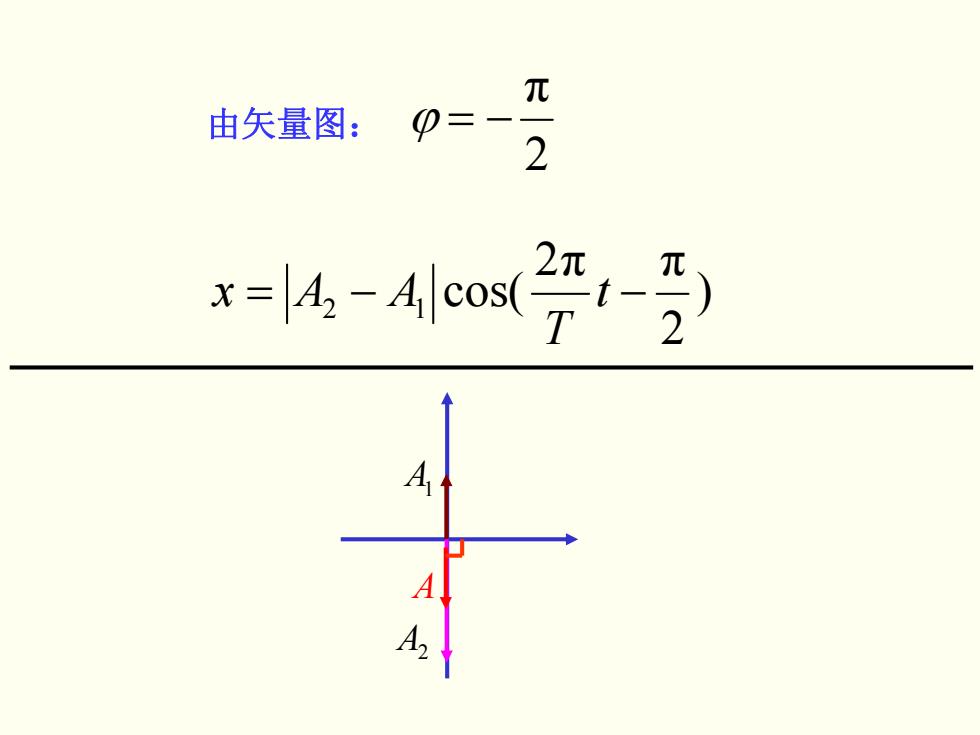
元 由矢量图: 2 x=4-4eo21-
) 2 2 ππ cos( −= 12 t − T AAx A1 A2 A 2 π 由矢量图: ϕ −=