
欧拉图的判别法 定理15.1无向图G是欧拉图当且仅当G是连通 的且所有顶点都是偶度的。 定理15.2无向图G是半欧拉图当且仅当G连通 且恰有两个奇度顶点
定理15.1 无向图G是欧拉图当且仅当G是连通 的且所有顶点都是偶度的。 定理15.2 无向图G是半欧拉图当且仅当G连通 且恰有两个奇度顶点. 欧拉图的判别法
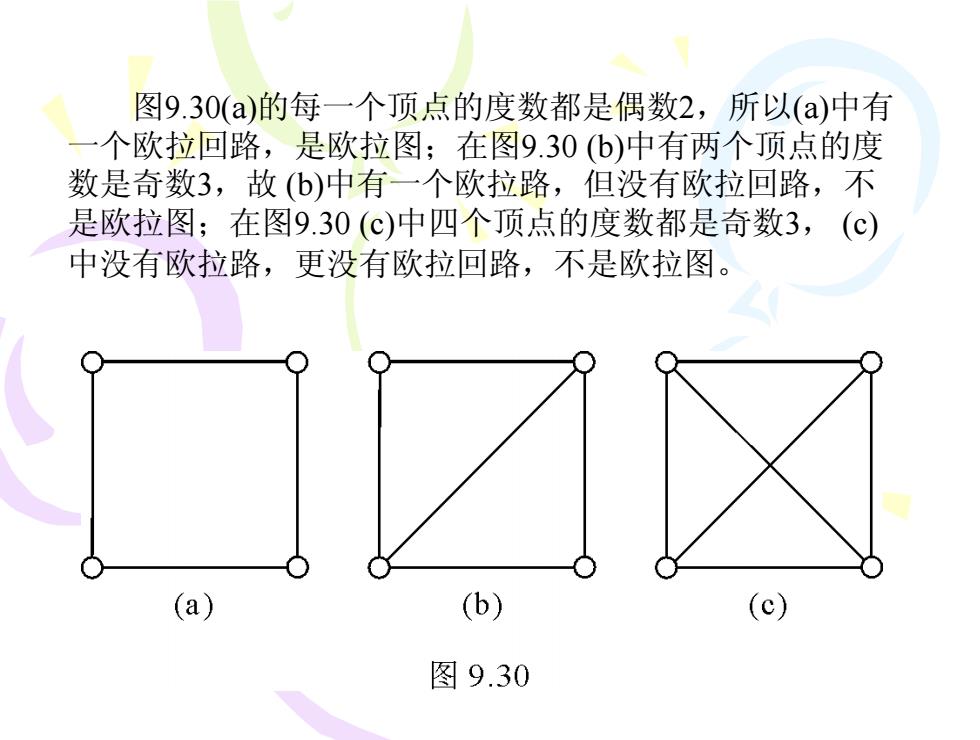
图9.30(a)的每一个顶点的度数都是偶数2,所以(a)中有 个欧拉回路,是欧拉图;在图9.30(b)中有两个顶点的度 数是奇数3,故(b)中有一个欧拉路,但没有欧拉回路,不 是欧拉图;在图9.30(C)中四个项点的度数都是奇数3,(c) 中没有欧拉路,更没有欧拉回路,不是欧拉图。 (a) (b) 图9.30
图9.30(a)的每一个顶点的度数都是偶数2,所以(a)中有 一个欧拉回路,是欧拉图;在图9.30 (b)中有两个顶点的度 数是奇数3,故 (b)中有一个欧拉路,但没有欧拉回路,不 是欧拉图;在图9.30 (c)中四个顶点的度数都是奇数3, (c) 中没有欧拉路,更没有欧拉回路,不是欧拉图

有向欧拉图的判别法 定理15.3有向图D是欧拉图当且仅当D强连通且 每个顶点的入度都等于出度 定理15.4有向图D是半欧拉图当且仅当D单向连通 且恰有两个奇度顶点,其中一个入度比出度大1,另一 个出度比入度大1,其余顶点的入度等于出度:
有向欧拉图的判别法 定理15.3 有向图D是欧拉图当且仅当D强连通且 每个顶点的入度都等于出度. 定理15.4有向图D是半欧拉图当且仅当D单向连通 且恰有两个奇度顶点, 其中一个入度比出度大1, 另一 个出度比入度大1, 其余顶点的入度等于出度
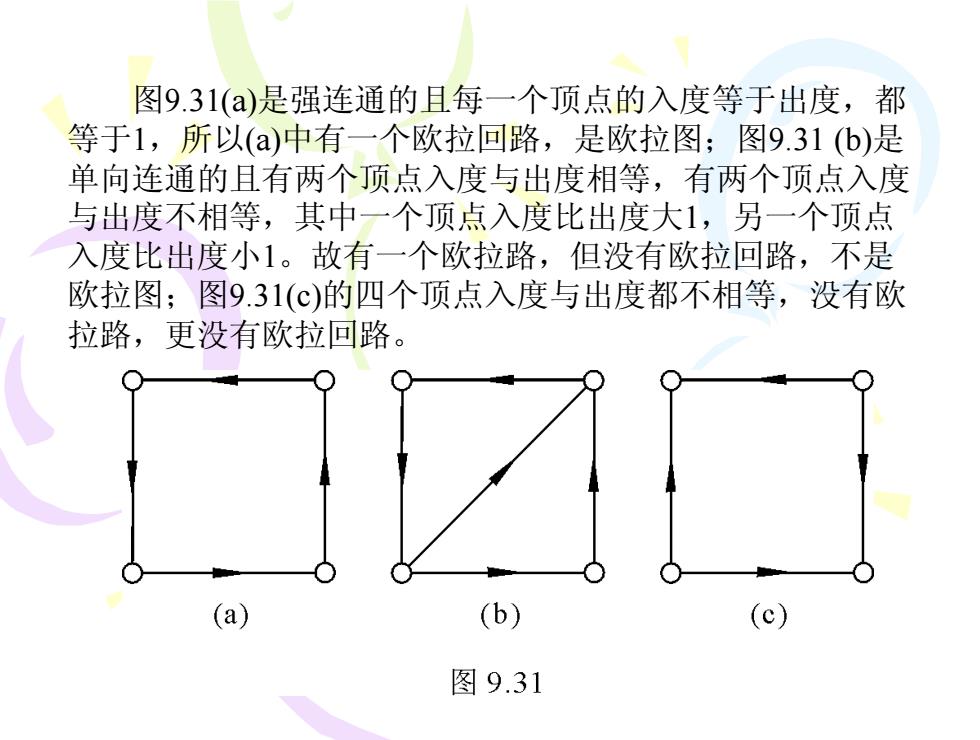
图9.31(a)是强连通的且每一个顶点的入度等于出度,都 等于1,所以(a)中有一个欧拉回路,是欧拉图:图9.31(b)是 单向连通的且有两个顶点入度与出度相等,有两个顶点入度 与出度不相等,其中一个顶点入度比出度大1,另一个顶点 入度比出度小1。故有一个欧拉路,但没有欧拉回路,不是 欧拉图;图9.31(c)的四个顶点入度与出度都不相等,没有欧 拉路,更没有欧拉回路。 (a) (b) (c) 图9.31
图9.31(a)是强连通的且每一个顶点的入度等于出度,都 等于1,所以(a)中有一个欧拉回路,是欧拉图;图9.31 (b)是 单向连通的且有两个顶点入度与出度相等,有两个顶点入度 与出度不相等,其中一个顶点入度比出度大1,另一个顶点 入度比出度小1。故有一个欧拉路,但没有欧拉回路,不是 欧拉图;图9.31(c)的四个顶点入度与出度都不相等,没有欧 拉路,更没有欧拉回路
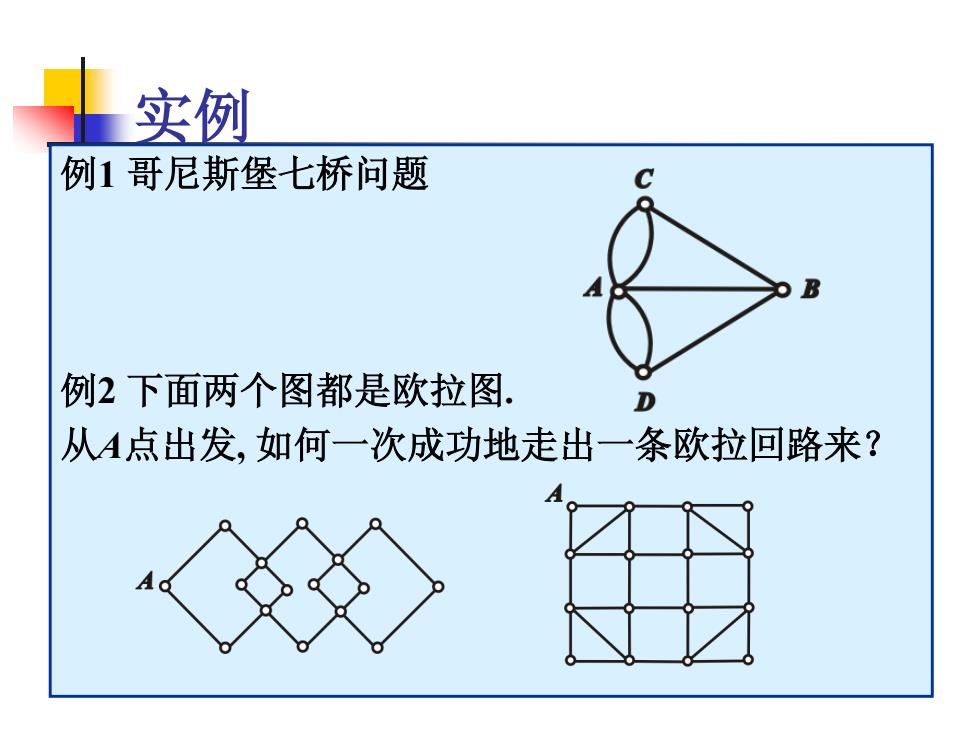
实例 例1哥尼斯堡七桥问题 例2下面两个图都是欧拉图. D 从A点出发,如何一次成功地走出一条欧拉回路来?
实例 例1 哥尼斯堡七桥问题 例2 下面两个图都是欧拉图. 从A点出发, 如何一次成功地走出一条欧拉回路来?