
3-11 一火箭垂直向上发射,它的气体质量排出率恒为5.00×102m0s1, 其中0是火箭最初的质量.火箭排出的气体相对于火箭的速率为5.00×10ms1 求发射10.0s后火箭的速率和高度.(重力略去不计) 分析由于火箭每秒钟排出气体的质量恒定,在:时刻火箭的质量m也就 确定.在重力忽略的情况下,火箭仅在推力udmidt作用下飞行.由于排气速率 恒定,由动力学方程mduldt=一udm/dt经一次积分后,可得火箭速率与质量 的关系式u=u加,因此,特定时间后火箭的速率即可求得:至于火箭的高 度,只需对速度关系式再进行一次积分即可得到。 解设火箭每秒钟排出气体的质量为是,在t时刻火箭的质量为m=m0一:. 由分析可知火箭的速率与质量的关系为 v uln 0 mo-kt (1) 故火箭发射t=10s后的速率 v=3.47×103m·s1 因v=dydt,将式(1)对时间t积分,并依据初始条件t=0时,y=0,可得火箭 发射10s后的高度 r109 0 m0206dt=1.53×10m

3一12铁路上有一静止的平板车,其质量为m',设平板车可无摩擦地在 水平轨道上运动.现有N个人从平板车的后端跳下,每个人的质量均为m,相 对平板车的速度均为4.问:在下列两种情况下,(1)N个人同时跳离:(2)一个 人、一个人地跳离,平板车的末速是多少?所得的结果为何不同,其物理原因是 什么? 分析由于地面没有摩,,对人与车组成的系统而言,人跳离车这一过程, 实质上是在水平轨道方向上的动量守恒问题.应用动量守恒定律时,取地面为参 考系(惯性系),而不能选取平板车(非惯性系).因此,在考虑人的动量时,必须是 相对于地面的动量.在每次跳车过程中,人与车之间有相互作用力,但由于时间 很短,因此,在短哲的冲力作用下,人、车的速度都有一次腺间的跃变,人的动量 由mo变为m(o'+),而车的动量由m'。变为m'o'.当N个人接连跳车时,为 了得到最终的车速,可利用数学上的递推公式进行处理, 解取平板车及N个人组成的系统,以地面为参考系,平板车的运动方向 为正方向,系统在该方向上满足动量守恒, 考患N个人同时跳车的情况.设跳车后平板车的速度为,则由动量守恒 定律得 0=m'o+Nm(o-4) U= m m'+Nm (1) 又考虑N个人一个接一个的跳车的情况.设当平板车上尚有n个人时的 速度为。,跳下一人后车速为。-1,在这一次跳车过程中,根据动量守恒有 (m'+nm)n=mvn-1+(t-1)m℃e-1+m(vn-1-4) (2) 由式(2)可解得递推公式 -1=y十 (3) n十m 显然,当车上有N个人时(即n=N),因尚未有人跳离平板车,故N=0:而车 上N个人全跳完时,车速为0.根据式(3)有 UN-1=0+m Nmu m N-2=w-1十 m'+(N-1)m“ 0=U1十7 十m 将上述各等式的两侧分别相加,整理后得 0= m'+nm n和1 由于 m'+nm≤m'+Nm n=1,2,3,…,N 故有 70>u 即N个人一个接一个地跳车时,平板车的末速0大于N个人同时跳下时平板 车的末速口.这是因为在N个人逐一跳离车时,车对地的速度逐次增加,导致跳 车者相对地面的速度也逐次增大,并对平板车所作的功也相应增大,因而平板车 得到的能量也大,其车速也大
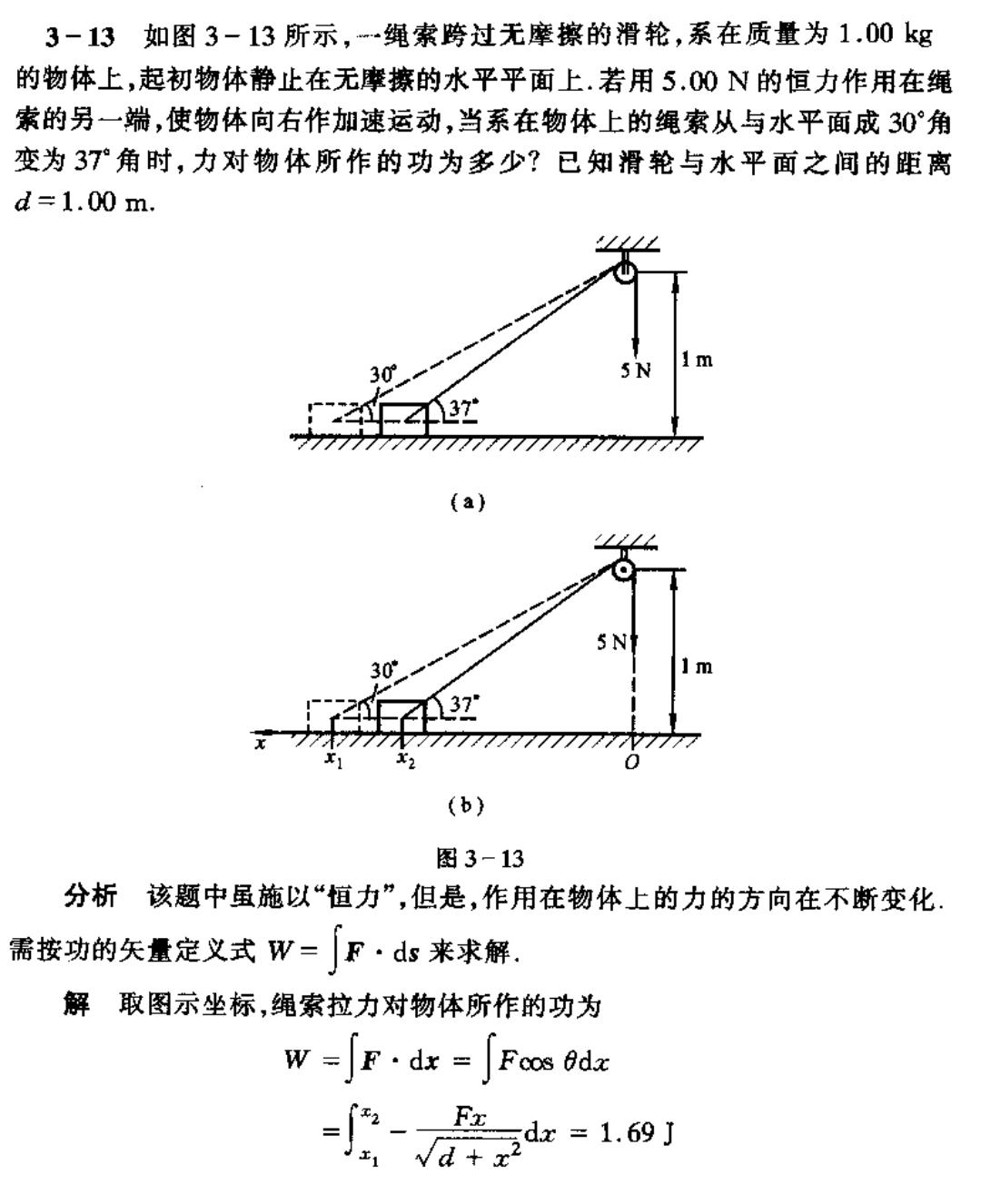
3-13如图3-13所示,…绳索跨过无摩擦的滑轮,系在质量为1.00kg 的物体上,起初物体静止在无摩擦的水平平面上.若用5.00N的恒力作用在绳 素的另一端,使物体向右作加速运动,当系在物体上的绳索从与水平面成30°角 变为3T角时,力对物体所作的功为多少?已知滑轮与水平面之间的距离 d=1.00m. 30 年红 777777777777777777777777777777 (a) N 30 】m 232 (b) 图3-13 分析该题中虽施以“恒力”,但是,作用在物体上的力的方向在不断变化, 需按功的矢量定义式W=F·ds来求解 解取图示坐标,绳索拉力对物体所作的功为 w=F·dx=Fcos8dz -产a如1w1