
第十二京电磁感成电磁场 思12.11如图所示,在磁感强度B=7.6×10-4T的均匀磁场中,故置一个线网。此线同由两 个半径均为3.7m且相互垂直的半圆成,磁感强度的方向与两半圆平面的夹角分别为62”和 28。若在4.5×0-?s的时问内磁场突架或至零,试间在此线图内的惩应电动势为多少? 思121分析:出各种原因在回路中所引起的感应电动势,均可由法拉第电磁感应定律求解, 即c:一芒-品B5包在聚相时度室下列机个问思: 【。回路必须是闭合的,所求得的电动势为回路的总电动势。 2,中应该是国路在任意时刻成任意位置处的础通量。它由心-∫B:dS计算对于均句磁 场则有巾-∫B:dS-心c0sB,其中ScOs8=S,为闭会回路在垂直于磁场的平面内的投能面 积.对于本题,中-5,c0sa+S:c0s0中B和0为两半图形平面法线,与B之间的夹角. 3.感应电动势的方向可由-地来判定,教材中已给出判定方法,为方便起见,所取回 d 毫的正向(飘时针成逆时针)应与穿过包路的B的方向满足右螺旋关扇,此时中恒为正值: 这对符号确定较为有利。 恶121解:迎着B的方向,取边时针为找圈回路的正向。由法拉第电磁感应定律 e (BS,cos0,+BS,cos0)=(S,cos0,+S,cos0,) 山-d d山 (S,c0s8,+Scos82)-4.91xl04V
第十二章电磁感应电磁场 题 12.1:如图所示,在磁感强度 7.6 10 T -4 B = 的均匀磁场中,放置一个线圈。此线圈由两 个半径均为3.7 cm 且相互垂直的半圆构成,磁感强度的方向与两半圆平面的夹角分别为 62 和 28 。若在 4.5 10 s -3 的时间内磁场突然减至零,试问在此线圈内的感应电动势为多少? 题 12.1 分析:由各种原因在回路中所引起的感应电动势,均可由法拉第电磁感应定律求解, 即 = − = − S d d d d d B S t t Φ 但在求解时应注意下列几个问题: 1.回路必须是闭合的,所求得的电动势为回路的总电动势。 2.Φ 应该是回路在任意时刻或任意位置处的磁通量。它由 = S Φ B dS 计算。对于均匀磁 场则有 d cos S Φ = = BS B S ,其中 S = S⊥ cos 为闭会回路在垂直于磁场的平面内的投影面 积。对于本题, 1 1 2 2 Φ = BS cos + BS cos 中 1 和 2 为两半圆形平面法线 n e 与 B 之间的夹角。 3.感应电动势的方向可由 t Φ d d − 来判定,教材中已给出判定方法。为方便起见,所取回 路的正向(顺时针或逆时针)应与穿过回路的 B 的方向满足右螺旋关系,此时 Φ 恒为正值, 这对符号确定较为有利。 题 12.1 解:迎着 B 的方向,取逆时针为线圈回路的正向。由法拉第电磁感应定律 ( cos cos ) 4.91 10 V cos cos d d cos cos d d d d 4 1 1 2 2 1 1 2 2 1 1 2 2 − + = = − = − = − + = − + S S t B S S t B BS BS t t Φ ( ) ( )

之0,说明感应电动势方向与回路正向一致 题122;一铁心上绕有线图100匝,已知铁心中磁通量与时间的关系为 中-(80xI0Wh)si(l00s'r,求在t-10xl0-s时,线图中的感应电动势。 题12,2解:线岁中总的感应电动势 6s-w 山 =(2.51V)e08(l00xs-y 当1=1.0×10-2s时,8=2.51V。 思123:如图所示,用一根处导线弯成半轻为r的一个半圆。使这根半圆形导找在磁感强度 为B的匀强磁杨中以顿辛了旋转,整个电路的电阻为R,求感应电蓬的表达式和最大做。 思123解:由于磁场是均匀的,故任意时刻穿过回路的磁通量为 )=中+cose 其中成等丁常量,S为半国面积, 0-中+-(%+2) W-我+行可Bos2喻+) 1 限指法拉第电酸多应定律,有5=一9-产历+ 因此可路中的感应电就为 10-£-r2 -sin(2+) 划感应电流的最大慎为 - R 恶124:有两根湘距为d的无限长平行直导线,它们通以大小相等近向相反的电流,且电流 均以业的变化率增长。若有一边长为d的正方形线医与两导线处于同一平面内,知图所示
0 ,说明感应电动势方向与回路正向一致 题 12.2 : 一铁心上绕有线圈 100 匝,已知铁心中磁通量与时间的关系为 Φ (8.0 10 Wb)sin(100 s )t −5 −1 = ,求在 1.0 10 s -2 t = 时,线圈中的感应电动势。 题 12.2 解:线圈中总的感应电动势 t t Φ N (2.51 V) cos(100 s ) d d −1 = − = 当 1.0 10 s -2 t = 时, = 2.51 V。 题 12.3:如图所示,用一根硬导线弯成半径为 r 的一个半圆。使这根半圆形导线在磁感强度 为 B 的匀强磁场中以频率 f 旋转,整个电路的电阻为 R,求感应电流的表达式和最大值。 题 12.3 解:由于磁场是均匀的,故任意时刻穿过回路的磁通量为 Φ(t) = Φ0 + BS cos 其中Φ0 等于常量,S 为半圆面积, ( 2 ) 0 0 = Φ +t = + ft cos(2 ) 2 1 ( ) 0 2 Φ t = Φ0 + r B ft + 根据法拉第电磁感应定律,有 sin(2 ) d d 0 2 2 = − = r fB ft + t Φ 因此回路中的感应电流为 ( ) sin(2 ) 0 2 2 = = ft + R r fB R I t 则感应电流的最大值为 R r fB I 2 2 m = 题 12.4:有两根相距为 d 的无限长平行直导线,它们通以大小相等流向相反的电流,且电流 均以 t I d d 的变化率增长。若有一边长为 d 的正方形线圈与两导线处于同一平面内,如图所示
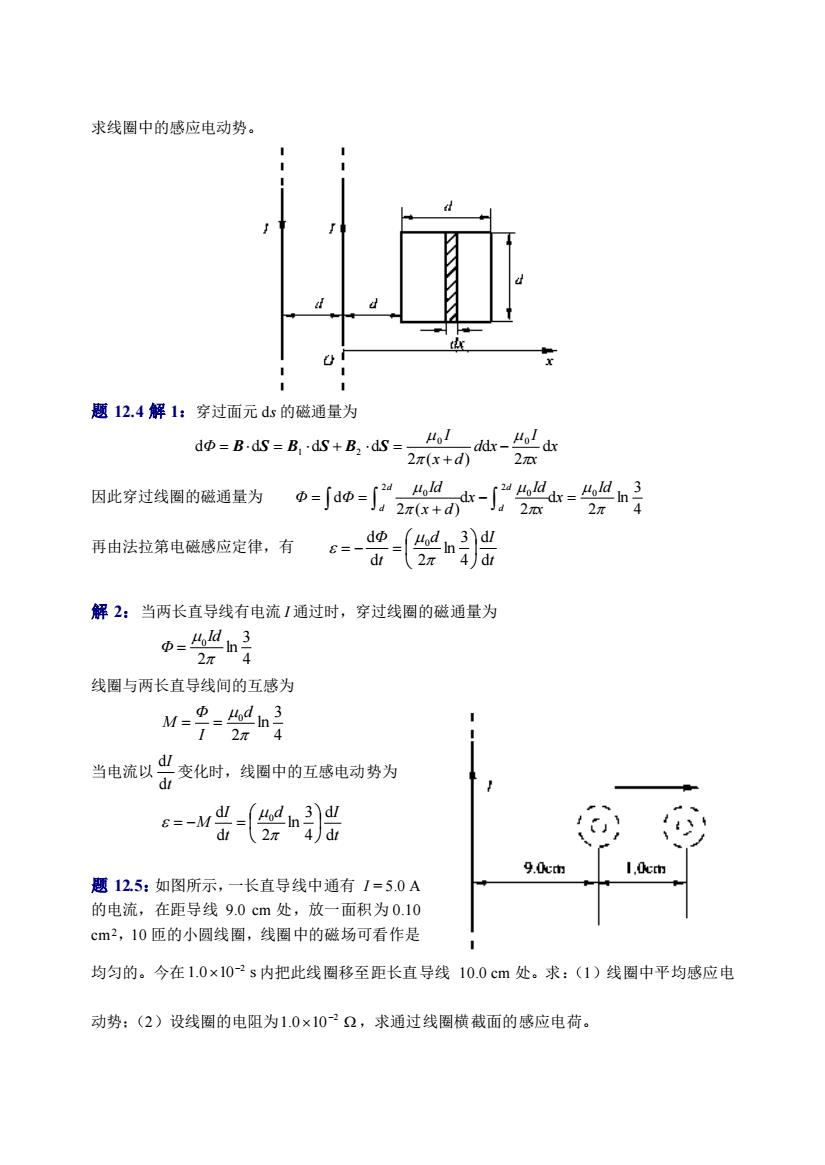
求线圈中的感应电动势, 题12,4解1:穿过面元ds的酸通量为 d=B-dS=B.ds+B,dS=Moldds-ol ds 2x(x+d) 因此等过线医的磁通量为 =小a地-广4-广尝=尝n 24 再由法拉第电酸感应定律,有 2=- d山 解2:当两长直导线有电流/通过时,家过线尚的题通量为 -44h 2x4 线圆与两长直线间的互感为 M-din3 12x4 当电流以”变化时,找图中的互感电动势为 dr 9.0w 思125:如图所示,一长直导线中通有1-5.0A 的电流,在距导线9.0cm处,放一面积为0.10 m2,10版的小因线园,线园中的磁场可看作是 均匀的,今在1.0×02s内把此线图移至距长直导线100cm处。求:(1)线图中平均感应电 动势:(2》设线图的电阻为10x01Q,求通过线圆横裁面的感应电荷
求线圈中的感应电动势。 题 12.4 解 1:穿过面元 ds 的磁通量为 x x I d x x d I Φ d 2 d 2 ( ) d d d d 0 0 1 2 − + = B S = B S + B S = 因此穿过线圈的磁通量为 4 3 ln 2 d 2 d 2 ( ) d 0 2 0 2 0 Id x x Id x x d Id Φ Φ d d d d − = + = = 再由法拉第电磁感应定律,有 t d I t Φ d d 4 3 ln d 2 d 0 = − = 解 2:当两长直导线有电流 I 通过时,穿过线圈的磁通量为 4 3 ln 2 0 Id Φ = 线圈与两长直导线间的互感为 4 3 ln 2 0 d I Φ M = = 当电流以 t I d d 变化时,线圈中的互感电动势为 t d I t I M d d 4 3 ln d 2 d 0 = − = 题 12.5:如图所示,一长直导线中通有 I = 5.0 A 的电流,在距导线 9.0 cm 处,放一面积为 0.10 cm2,10 匝的小圆线圈,线圈中的磁场可看作是 均匀的。今在 1.0 10 s −2 内把此线圈移至距长直导线 10.0 cm 处。求:(1)线圈中平均感应电 动势;(2)设线圈的电阻为 −2 1.0 10 ,求通过线圈横截面的感应电荷
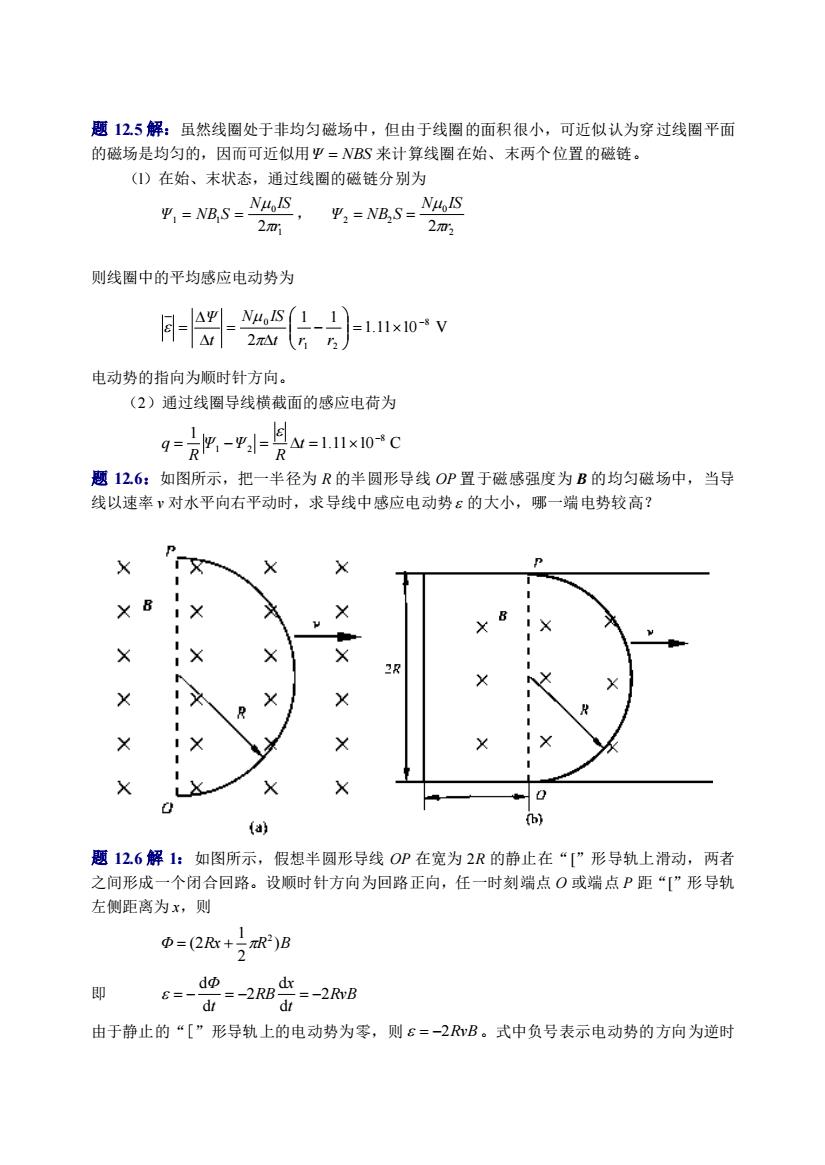
题125解:屁然线图处于非均匀磁场中,但由于线图的面积很小,可近似认为穿过线图平面 的毯场是均匀的,因而可近似用平=NBS来计算线园在始、末两个位置的琶链。 《)在始、末状态,通过线图的磁链分别为 %=BS=区 =NB S= NupIS 28 281 则线圈中的平均感应电动势为 -111×10*V 电动势的粉向为顺时针方向。 (2》通过线国学线横甚面的感应电荷为 q=严-g-月y=1x0c R 题126:如图所示,把一半径为R的率国形导线OP置于磁感强度为B的均匀磁场中,当导 线以庭率¥对水平向右平动时,求导线中感应电动势:的大小,围端电势较高? i (aj 思126解1:如图所示,假州半国形导线0OP在宽为2R的静止在“[”形导轨上滑动,两者 之间形成一个闭合回路。设顺时针方向为回路正向。任一时刻操点O或端点P距“[形导轨 左侧便离为x,则 =(2+二R2)B 2 即 d 6=- 2=-2RB业=-28 d山 由于静止的“[”形导轨上的电动势为零,则E=-2B。式中负号表示电动势的方向为逆时
题 12.5 解:虽然线圈处于非均匀磁场中,但由于线圈的面积很小,可近似认为穿过线圈平面 的磁场是均匀的,因而可近似用 Ψ = NBS 来计算线圈在始、末两个位置的磁链。 (l)在始、末状态,通过线圈的磁链分别为 1 0 1 1 2 r N IS Ψ NB S = = , 2 0 2 2 2 r N IS Ψ NB S = = 则线圈中的平均感应电动势为 1.11 10 V 1 1 2 8 1 2 0 − = − = = t r r N IS t Ψ 电动势的指向为顺时针方向。 (2)通过线圈导线横截面的感应电荷为 1.11 10 C 1 8 1 2 − = − = t = R Ψ Ψ R q 题 12.6:如图所示,把一半径为 R 的半圆形导线 OP 置于磁感强度为 B 的均匀磁场中,当导 线以速率 v 对水平向右平动时,求导线中感应电动势 的大小,哪一端电势较高? 题 12.6 解 1:如图所示,假想半圆形导线 OP 在宽为 2R 的静止在“[”形导轨上滑动,两者 之间形成一个闭合回路。设顺时针方向为回路正向,任一时刻端点 O 或端点 P 距“[”形导轨 左侧距离为 x,则 Φ Rx R )B 2 1 (2 2 = + 即 RvB t x RB t Φ 2 d d 2 d d = − = − = − 由于静止的“[”形导轨上的电动势为零,则 = −2RvB 。式中负号表示电动势的方向为逆时
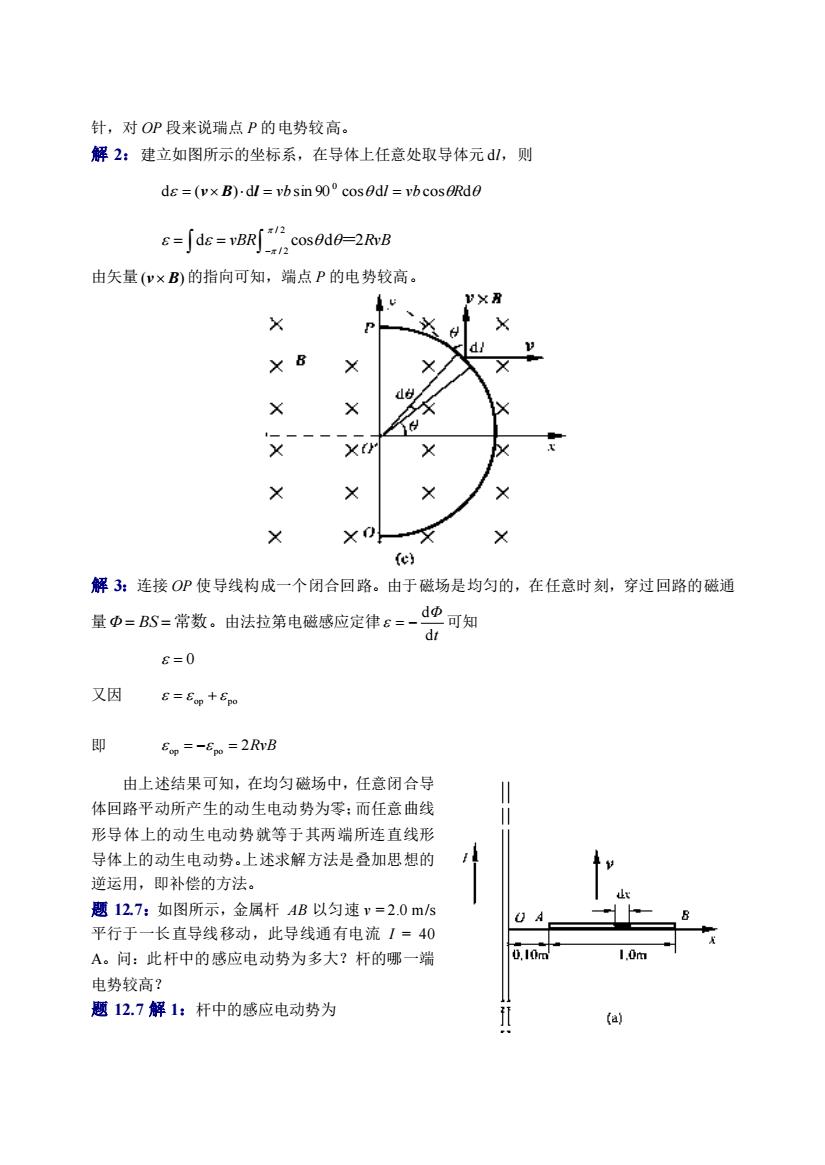
针,对OP段米说瑞点P的电势较高。 解2:建立如图所示的坐标系,在导体上任意处取导体元山,则 ds=(v×B)dl=vbsin0°cos0dl=cosRd8 de0vB 由矢量(x的指向可知。端点P的电势较高。 X X B X e 解3:连接O使导线构咸一个闭合回路。出于磁场是均匀的,在任意时刻,穿过回路的磁通 量巾一S-常数。由法拉第电磁感应定律6一d地可知 d山 5-0 又因 E=Ep+Ep 即 5p=-8a=2RB 由上述结果可知,在均匀磁场中,任意闭合导 体回路平动所产生的动生电动势为零:而任意曲战 形导体上的动生电动势就等于其两端所连直找形 导体上的动生电动势。上运求解方法是叠加思想的 逆运用,即补偿的方法, 题127:如图所示,金属杆AB以匀速”=2.0ms 平行于一长直导线移动,北导线通有电瓷/一40 A。问:此杆中的感应电动势为多大?杆的愿一端 0,0 电势较高? 思12.7解1:杆中的感应电动势为 a
针,对 OP 段来说瑞点 P 的电势较高。 解 2:建立如图所示的坐标系,在导体上任意处取导体元 dl,则 d ( ) d sin 90 cos d cos d 0 = v B l = vb l = vb R − = = / 2 / 2 d cos d 2 vBR = RvB 由矢量 (v B) 的指向可知,端点 P 的电势较高。 解 3:连接 OP 使导线构成一个闭合回路。由于磁场是均匀的,在任意时刻,穿过回路的磁通 量 Φ = BS =常数 。由法拉第电磁感应定律 t Φ d d = − 可知 = 0 又因 op po = + 即 op = − po = 2RvB 由上述结果可知,在均匀磁场中,任意闭合导 体回路平动所产生的动生电动势为零;而任意曲线 形导体上的动生电动势就等于其两端所连直线形 导体上的动生电动势。上述求解方法是叠加思想的 逆运用,即补偿的方法。 题 12.7:如图所示,金属杆 AB 以匀速 v = 2.0 m/s 平行于一长直导线移动,此导线通有电流 I = 40 A。问:此杆中的感应电动势为多大?杆的哪一端 电势较高? 题 12.7 解 1:杆中的感应电动势为