
家庭馆亚 6 直线和圆的位置关系 第2课时 )线的判定、三角形的内勿圆
6 直线和圆的位置关系 第2课时 切线的判定、三角形的内切圆

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.过半径外端且垂直 于这条半径的直线是圆的切线 温馨提示 1切线必须同时具备以下两个条件:(1)经过半径的外端;(2) 垂直于半径 2.切线的判定方法:1)直线与圆有唯一公共点;2)直线到圆 心的距离等于该圆的半径;3)切线的判定定理, 导航页
导航页 基础自主梳理 1.过半径外端且 于这条半径的直线是圆的切线. 温馨提示 1.切线必须同时具备以下两个条件:(1)经过半径的外端;(2) 垂直于半径. 2.切线的判定方法:(1)直线与圆有唯一公共点;(2)直线到圆 心的距离等于该圆的半径;(3)切线的判定定理. 垂直

基础自主梳理 2.与三角形各边都相切 的圆叫做三角形的内切圆,内 切圆的圆心是三角形三条角平分线的交点,叫做三角形的 内心. 易错警示 1任何一个三角形都只有一个内心,三角形的内心在三角形 的内部 2.一个三角形只有一个内切圆,而一个圆有无数个外切三角 形. 3.等边三角形的内心和外心重合 导航页
导航页 基础自主梳理 2.与三角形各边都 的圆叫做三角形的内切圆,内 切圆的圆心是三角形三条 的交点,叫做三角形的 内心. 易错警示 1.任何一个三角形都只有一个内心,三角形的内心在三角形 的内部. 2.一个三角形只有一个内切圆,而一个圆有无数个外切三角 形. 3.等边三角形的内心和外心重合. 相切 角平分线
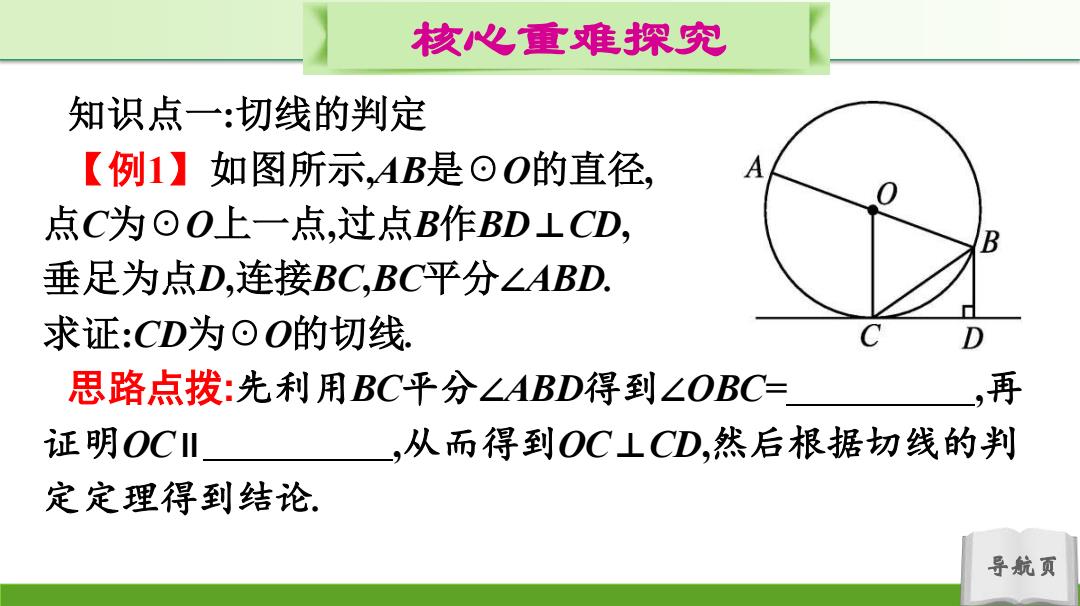
核心重难探究 知识点一:切线的判定 【例1】如图所示,AB是⊙O的直径, 点C为⊙O上一点,过点B作BD⊥CD, 垂足为点D,连接BC,BC平分∠ABD. 求证:CD为⊙O的切线 思路点拨:先利用BC平分∠ABD得到∠OBC= ,再 证明OCⅢ ,从而得到OC⊥CD,然后根据切线的判 定定理得到结论. 导航页
导航页 核心重难探究 知识点一:切线的判定 【例1】如图所示,AB是☉O的直径, 点C为☉O上一点,过点B作BD⊥CD, 垂足为点D,连接BC,BC平分∠ABD. 求证:CD为☉O的切线. 思路点拨:先利用BC平分∠ABD得到∠OBC= ,再 证明OC∥ ,从而得到OC⊥CD,然后根据切线的判 定定理得到结论