
例将二进制数1011.01转换成 十进制数。 解:将每一位二进制数乘以位权,然后 相加,可得 (1011.01)B=1×23+0×22+1×21+ 1×20+1×2-1+0X2-2 (11.25)D 2006年 新疆大学信息科学与工程学院 16 《数字电路课题组》
2006年 新疆大学信息科学与工程学院 《数字电路课题组》 16 例 将二进制数1011.01转换成 十进制数。 解:将每一位二进制数乘以位权,然后 相加,可得 (1011.01)B = 1×2 3 + 0×2 2 + 1×2 1 + 1×2 0+1×2-1+0×2-2 =(11.25)D
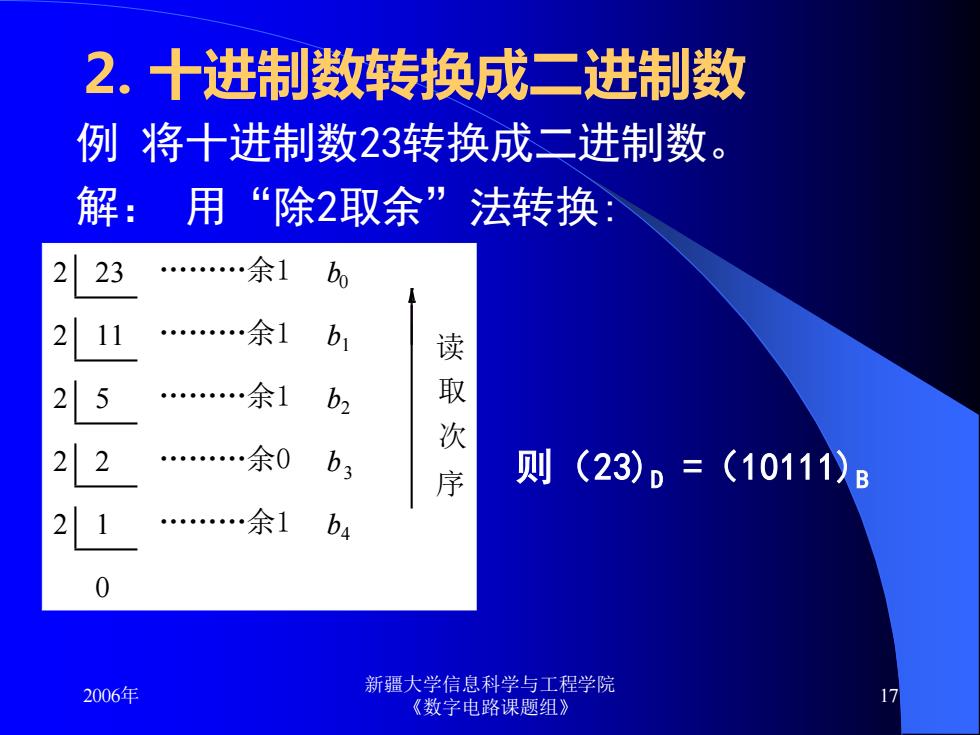
2.十进制数转换成二进制数 例将十进制数23转换成二进制数。 解:用“除2取余”法转换: 2 23 .余1 211 .余1 b 25 .余1 b2 取 次 22 .余0 序 则(23)D=(10111)B 21 .余1 2006年 新疆大学信息科学与工程学院 《数字电路课题组》
2006年 新疆大学信息科学与工程学院 《数字电路课题组》 17 23 11 5 2 1 2 2 2 2 2 .余0 .余1 .余1 .余1 .余1 0 b b b b b 0 1 2 3 4 读 取 次 序 例 将十进制数23转换成二进制数。 解: 用“除2取余”法转换: 2. 十进制数转换成二进制数 则(23)D =(10111)B

3、十进制数转换成二进制数 转换方法:整数部分采用除基数取余法; 小数部分采用乘基数取整法。 例(286.8125)1转换成二进制数的过程如 下所示 2006年 新疆大学信息科学与工程学院 18 《数字电路课题组》
2006年 新疆大学信息科学与工程学院 《数字电路课题组》 18 3、十进制数转换成二进制数 转换方法:整数部分采用除基数取余法; 小数部分采用乘基数取整法。 例(286.8125 )10转换成二进制数的过程如 下所示:

例二进制与十进制之间的转换 对于整数部分:除2取余 2286 余数 2 143 0(最低位) 2 71 35 2 8 0 2 0 0 '.(286)10=(100001110)2 1(录高位) 2006年 新疆大学信息科学与工程学院 19 《数字电路课题组》
2006年 新疆大学信息科学与工程学院 《数字电路课题组》 19 例二进制与十进制之间的转换 2 286 2 143 0 (最低位) 2 71 1 2 35 1 2 17 1 2 8 0 2 4 0 2 2 0 2 1 0 0 1 (最高位) 余数 ∴(286)10 = (100001110)2 对于整数部分:除2取余

二进制与十进制之间的转换 对于小数部分:乘2取整 0.8125×2=1.625取出整数1 (景高位》 1.625×2=1.25 取出整数1 0.25×2=0.5 取出整数0 0.5×2=1.0 取出整数1 (景低位) (0.8125)10=(0.1101)2 则(286.8125)10(100011110.1101) 2 2006年 新疆大学信息科学与工程学院 20 《数字电路课题组》
2006年 新疆大学信息科学与工程学院 《数字电路课题组》 20 对于小数部分: 乘2取整 0. 8125×2=1.625 取出整数1 (最高位) 1. 625×2=1.25 取出整数1 0.25×2=0.5 取出整数0 0. 5×2=1.0 取出整数1 (最低位) ∴ (0.8125 )10 = (0.1101)2 则(286.8125)10= (100011110.1101) 2 二进制与十进制之间的转换