
1.1.1二进制 ●二进制数字符号:0、1权:2的幂 ●二进制的基数:2,计数规律:逢二进一。 任意一个二进制数可以表示成 (S)2k2+kn12m-1+.+k,21+k20 +k,21+.+kn2m 其中:k只能取0或1,它由(S),决定, m,n为正整数,表示权。 2006年 新疆大学信息科学与工程学院 《数字电路课题组》
2006年 新疆大学信息科学与工程学院 《数字电路课题组》 11 ⚫二进制数字符号:0、1 权:2的幂 ⚫二进制的基数:2,计数规律:逢二进一。 任意一个二进制数可以表示成 (S)2 =kn 2 n+kn-1 2 n-1+.+k1 2 1+k0 2 0 +k-1 2 -1+.+k-m 2 -m 其中:ki只能取0或1,它由(S)2决定, m,n为正整数,表示权。 1.1.1二进制

1.1.2八进制 数字符号:0~7 计数规则:逢八进 ●基数:8权:8的幂 任意一个八进制数可以表示成 (S)gk8n+knm-181+.+k,81+k80 +k,81+.+k8m 其中:k,可取0,1,2, 7八个数之 它由()。决定。m和n为正整数,表示权。 2006年 新疆大学信息科学与工程学院 12 《数字电路课题组》
2006年 新疆大学信息科学与工程学院 《数字电路课题组》 12 数字符号:0~7 计数规则:逢八进一 ⚫基数:8 权:8的幂 ⚫ 任 意 一 个 八 进 制 数 可 以 表 示 成 (S)8 =kn 8 n+kn-1 8 n-1+.+k1 8 1+k0 8 0 +k-1 8 -1+.+k-m 8 -m 其中:ki可取0,1,2,.,7八个数之一, 它由(S)8 决定。m和n为正整数,表示权。 1.1.2 八进制

1.1.3十六进制 数字符号:09、A、B、C、D、E、F 十六进制数的基数:16,计数规律:逢十六 进一。权:16的幂 任意一个十六进制数可以表示成 (S)16kn16+kn-116-1+.+k1161+k160 +k,161+.+km16m 其中:k可取0,1,2,.,9,A,B,C,D, E,F等十六个数码、字母之 一,它由(S)16决 定; m和n为正整数,表示权 2006年 新疆大学信息科学与工程学院 13 《数字电路课题组》
2006年 新疆大学信息科学与工程学院 《数字电路课题组》 13 1.1.3 十六进制 数字符号:0~9、A、B、C、D、E、F 十六进制数的基数:16,计数规律:逢十六 进一。权:16的幂 任意一个十六进制数可以表示成 (S)16=kn 16n+kn-1 16n-1+.+k1 161+k0 160 +k-1 16-1+.+k-m 16-m 其中:ki可取0,1,2,.,9,A,B,C,D, E,F等十六个数码、字母之一,它由 (S)16决 定;m和n为正整数,表示权
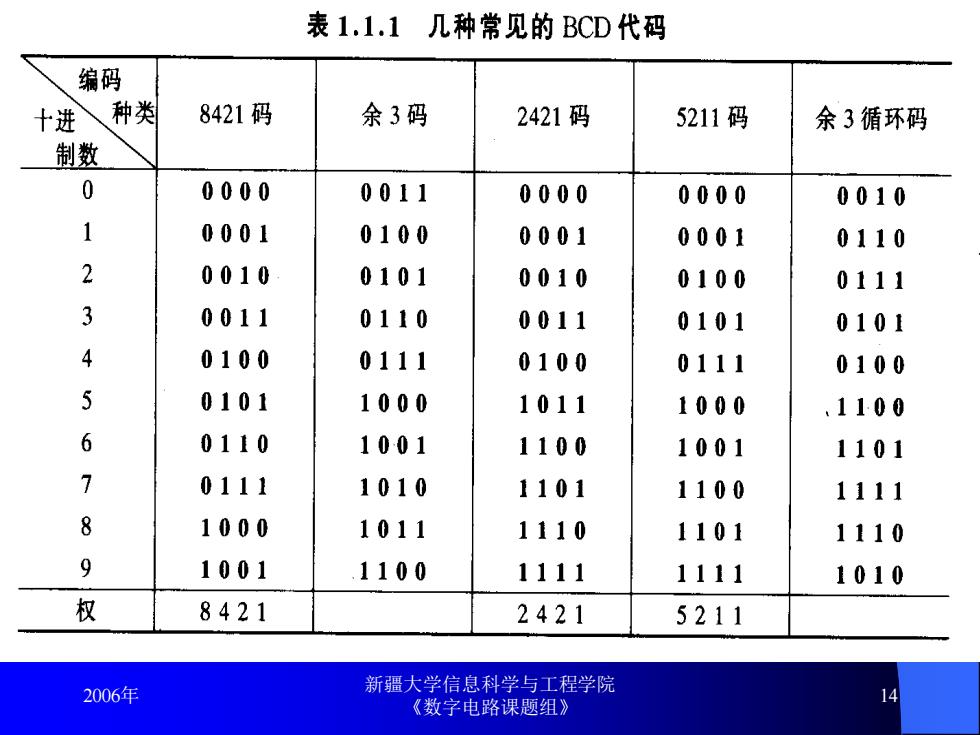
表1.1.1 几种常见的BCD代码 编码 十进 种类 8421码 余3码 2421码 5211码 余3循环码 制数 0 0000 0011 0000 0000 0010 1 0001 0100 0001 0001 0110 2 0010 0101 0010 0100 0111 3 0011 0110 0011 0101 0101 4 0100 0111 0100 0111 0100 5 0101 1000 1011 1000 .1100 6 0110 1001 1100 1001 1101 7 0111 1010 1101 1100 1111 8 1000 1011 1110 1101 1110 9 1001 1100 1111 1111 1010 权 8421 2421 5211 2006年 新疆大学信息科学与工程学院 14 《数字电路课题组》
2006 年 新疆大学信息科学与工程学院 《数字电路课题组》 14

1.1.4不同数制之间的相互转换 一、二进制与十进制的转换 1、二进制转换成十进制 转换方法:按权展开求和。 例1.2.1将二进制数10011.101转换成十进制数。 解:将每一位二进制数乘以位权,然后相加, 可得 (10011.101)B=1×24+0×23+0×22+1×21+ 1×20+1×2-1+0×2-2+1X2-3 (19.625)D 2006年 新疆大学信息科学与工程学院 《数字电路课题组》
2006年 新疆大学信息科学与工程学院 《数字电路课题组》 15 1.1.4 不同数制之间的相互转换 一、二进制与十进制的转换 1、二进制转换成十进制 转换方法:按权展开求和。 例1.2.1将二进制数10011.101转换成十进制数。 解:将每一位二进制数乘以位权,然后相加, 可得 (10011.101)B=1×2 4+0×2 3+0×2 2+1×2 1+ 1×2 0+1×2-1+0×2-2+1×2-3 =(19.625)D