
导期 【思考辨析】 判断下列说法是否正确,正确的在后面的括号里画“√”,错误 的画“X” (1)三条平行线可以确定一个平面.(×) (2)圆上的三点确定一个平面(V√) (3)四边形是平面图形.(X) (4)两条相交直线可以确定一个平面.(√)
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号里画“√” ,错误 的画“×” . (1)三条平行线可以确定一个平面.( ) (2)圆上的三点确定一个平面.( ) (3)四边形是平面图形.( ) (4)两条相交直线可以确定一个平面.( ) × √ × √
导 课堂·重难突破 探究一平面的基本事实(公理)的理解 【例1】如图,在正方体ABCD-A1B1C1D1中,正方形ABCD与 A1B1CD1的中心分别为O,O判断下列说法是否正确,并说明 理由。 ①直线AC在平面CC1B1B内; ②平面AA1C1C与平面BBD1D的交线为 001; ③由点A,O,C可以确定一个平面;
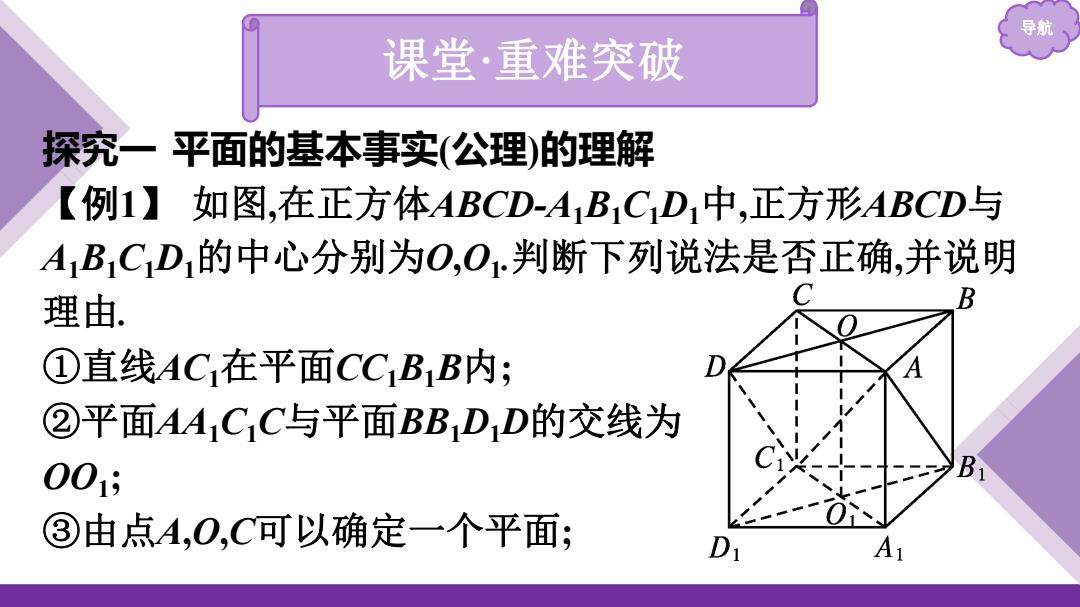
导航 课堂·重难突破 探究一 平面的基本事实(公理)的理解 【例1】 如图,在正方体ABCD-A1B1C1D1中,正方形ABCD与 A1B1C1D1的中心分别为O,O1 .判断下列说法是否正确,并说明 理由. ①直线AC1在平面CC1B1B内; ②平面AA1C1C与平面BB1D1D的交线为 OO1; ③由点A,O,C可以确定一个平面;

④由点A,C,B,确定的平面是ADCB1 ⑤若直线l是平面AC内的直线,直线m是平面D,C内的直线,若l 与m相交,则交点一定在直线CD上; ⑥由点A,C1,B确定的平面与由点A,C1,D确定的平面是同一平 面. 分析:首先弄清正方体中点、线、面的关系,再结合平面的基 本事实、推论解答
导航 ④由点A,C1 ,B1确定的平面是ADC1B1; ⑤若直线l是平面AC内的直线,直线m是平面D1C内的直线,若l 与m相交,则交点一定在直线CD上; ⑥由点A,C1 ,B1确定的平面与由点A,C1 ,D确定的平面是同一平 面. 分析:首先弄清正方体中点、线、面的关系,再结合平面的基 本事实、推论解答

解:①错误.假设AC1C平面CC1B1B,则A∈平面CC1B1B, 与事实矛盾,所以AC4平面CC1B1B. ②正确.O,01是两平面的两个公共点。 ③错误因为A,O,C三点共线,所以点A,O,C不能确定一个平面. ④正确..A,C1,B1不共线,.确定平面α. 又AB1C1D为平行四边形,设AC1,B1D相交于点O3,而 O3∈a,B1∈a,∴.B1O3Ca.而D∈B1O3,.D∈a. ⑤正确.若l与m相交,则交点是两平面的公共点,而直线CD为 两平面的交线,所以交点一定在直线CD上 ⑥正确理由同④
导航 解:①错误.假设AC1⊂平面CC1B1B,则A∈平面CC1B1B, 与事实矛盾,所以AC1⊄ 平面CC1B1B. ②正确.O,O1是两平面的两个公共点. ③错误.因为A,O,C三点共线,所以点A,O,C不能确定一个平面. ④正确.∵A,C1 ,B1不共线,∴确定平面α. 又AB1C1D为平行四边形,设AC1 ,B1D相交于点O3 ,而 O3∈α,B1∈α,∴B1O3⊂α.而D∈B1O3 ,∴D∈α. ⑤正确.若l与m相交,则交点是两平面的公共点,而直线CD为 两平面的交线,所以交点一定在直线CD上. ⑥正确.理由同④