Trade Initial investment Value on day T Buy stock -5010.000 10.000Sy Borrow funds 500.000 -50,00e59036时j=-506,202.54 Receive cash dividends on day, and re-invest at risk-free rate until day T 40,000e056036=40,330.12 Value of position 0 10.000S7-506,202.54+40,330.12

结论和一些准则 >持有成本收益一般来说,包括两个部分 (1)成本:金融资产的利息和非金融资产的存储 成本。 >利息部分通常表现为比率的形式,如果我们 在今天借款买入资产,在时刻T我们每单位资 产负债eT。 > (②)收益:金融资产的收入或有形资产的便利 收益。 > 收入和非利息现金流既可表示为资产价格的 一个连续比例,、也可表示为离散现金流,这 取决于基础资产的特征
结论和一些准则 ➢ 持有成本/收益一般来说,包括两个部分 ➢ (1)成本:金融资产的利息和非金融资产的存储 成本。 ➢ 利息部分通常表现为比率的形式,如果我们 在今天借款买入资产,在时刻T我们每单位资 产负债e rT 。 ➢ (2)收益:金融资产的收入或有形资产的便利 收益。 ➢ 收入和非利息现金流既可表示为资产价格的 一个连续比例,也可表示为离散现金流,这 取决于基础资产的特征

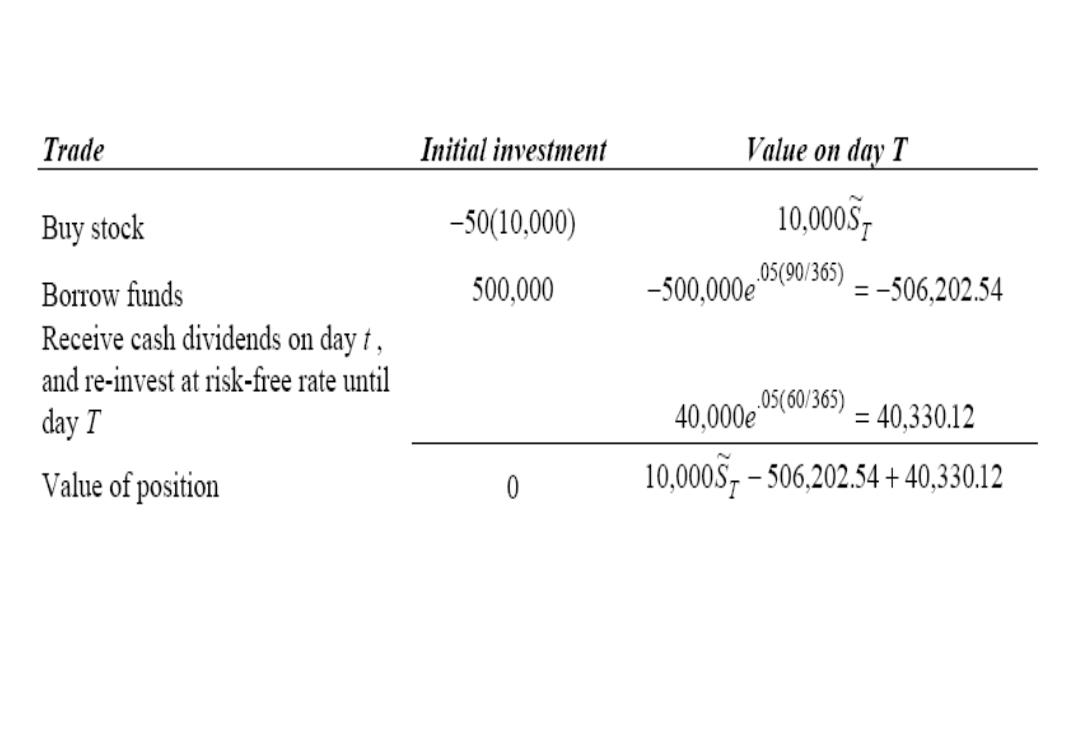
表41:利用连续比率离散现金流的净持有成本假设,计算杠杠化资产在时刻T 的未来价值。假设所有资产按照不变的连续利率计算利息成本。: 资产类型 建议模型 期末价值 非利息持有成本收益解释 股票 一单个股票或者 离散现金流 Sr-(Se"T-FVD) 对于单个普通股股票或 范围较小的股票组合 范围较窄的股票指数,收益 按照时刻t支付的离散型 现金股息I增长,股息按照 无风险利率一直持有至时 刻即Fn=∑1e-t). 股票组合 连续比率 ST-Se0-DT 对于范围广泛的股票组合, 收益按照固定的连续股息 收益率累积

债券 离散现金流 S,-(SeT-FD对于附息债券,收益按照时 刻t支付的离散型现金股 息I增长,利息按照无风险 利率一直持有至时刻T,即 FVI- ∑1,er- 外汇 连续比率 ST-Sel-OT 对于外汇存款,收益按照固 定的连续国外利率累积。 商品 离散现金流 Sr-(Se"T-FVD) 对于大多数有形商品,需要 支付存储成本(如仓库租金和 保险费),也会有便利收益。 此时,F是便利收益的未来 值减去离散型存储成本的未 来价值,即FV=FV(便利收 益)FV(存储成本)。尽管存储 成本可以设定为离散现金流, 但便利收益(如黄金租赁率)》 可设定为一个比率。一

4.2远期合约定价 >远期合同:在未来时刻T按照当前约定的价格 由卖方向买方交付基础资产的合同。 >本节的目的是在连续和离散净持有成本假设 下,推导时刻T之前对应于基础资产价格的远 期合约价格 。 我们用代表当前远期合同的价格,其在T时 >手 刻的价格表示为。到期的远期合同价格必 定与基础资产的侨格相同,即方=5
4.2 远期合约定价 ➢ 远期合同:在未来时刻T按照当前约定的价格 由卖方向买方交付基础资产的合同。 ➢ 本节的目的是在连续和离散净持有成本假设 下,推导时刻T之前对应于基础资产价格的远 期合约价格。 ➢ 我们用f代表当前远期合同的价格,其在T时 刻的价格表示为 。到期的远期合同价格必 定与基础资产的价格相同,即 ~ T f ~ ~ T T f S =