
第7章标准化期权 的解析法定价 朱子川接小波张翠萍 杨杨
第7章 标准化期权 的解析法定价 朱子川 接小波 张翠萍 杨杨

背景 第6章中,推导了期权价格关系式。仅指明了价格的边界, 而非精确的期权价值。本章推导欧式期权的定价公式,将该 公式用于风险管理,如何估计定价公式中的参数。 女 期权的定价也是未来现金流的现值。看涨期权的预期现金流 取决于:基础资产经风险调整的预期价格升值率。贴现率是期 权经风险调整的预期回报率。该传统定价法的一个问题是, 要准确估计风险调整的预期回报参数是非常困难的 1973年,随着Black和Scholes(1973)以及Merton(1973) (BSM)在期权和其基础资产之间构建一个无风险套期保值, 期权定价就与个人风险偏好无关,假设个体是风险中性的。 所有资产的预期回报率等于它们的无风险利率
背景 ❖ 第6章中,推导了期权价格关系式。仅指明了价格的边界, 而非精确的期权价值。本章推导欧式期权的定价公式,将该 公式用于风险管理,如何估计定价公式中的参数。 ❖ 期权的定价也是未来现金流的现值。看涨期权的预期现金流 取决于:基础资产经风险调整的预期价格升值率。贴现率是期 权经风险调整的预期回报率。该传统定价法的一个问题是, 要准确估计风险调整的预期回报参数是非常困难的。 ❖ 1973年,随着Black和Scholes (1973)以及Merton (1973) (BSM)在期权和其基础资产之间构建一个无风险套期保值, 期权定价就与个人风险偏好无关,假设个体是风险中性的。 所有资产的预期回报率等于它们的无风险利率

内容 第一节风险中性定价的直觉分析 。第二节给定正态分布回报率的均值和方差, 推导了资产预期价值的表达式。 ·第三节欧式看涨期权的定价公式。 ·第四节欧式看跌期权的定价公式。 ~第五节说明如何利用期权定价公式去度量期 权的风险特征。 心最后一节是结论
内容 ❖ 第一节风险中性定价的直觉分析 ❖ 第二节给定正态分布回报率的均值和方差, 推导了资产预期价值的表达式。 ❖ 第三节欧式看涨期权的定价公式。 ❖ 第四节欧式看跌期权的定价公式。 ❖ 第五节说明如何利用期权定价公式去度量期 权的风险特征。 ❖ 最后一节是结论

7.1风险中性定价的直觉分析 ÷7.1.1利用二项式模型构建无风险保值组合 ·欧式看涨期权,三个月后X=40。假设S=40, 三个月后资产的价格是45或35。这些资产价格 列于下图7-1.3个月后为45,则看涨期权价值 为5;如果资产价格3个月后为35,期权价值为 0
7.1 风险中性定价的直觉分析 ❖ 7.1.1 利用二项式模型构建无风险保值组合 ❖ 欧式看涨期权,三个月后X=40。假设S=40, 三个月后资产的价格是45或35。这些资产价格 列于下图7-1。3个月后为45,则看涨期权价值 为5;如果资产价格3个月后为35,期权价值为 0
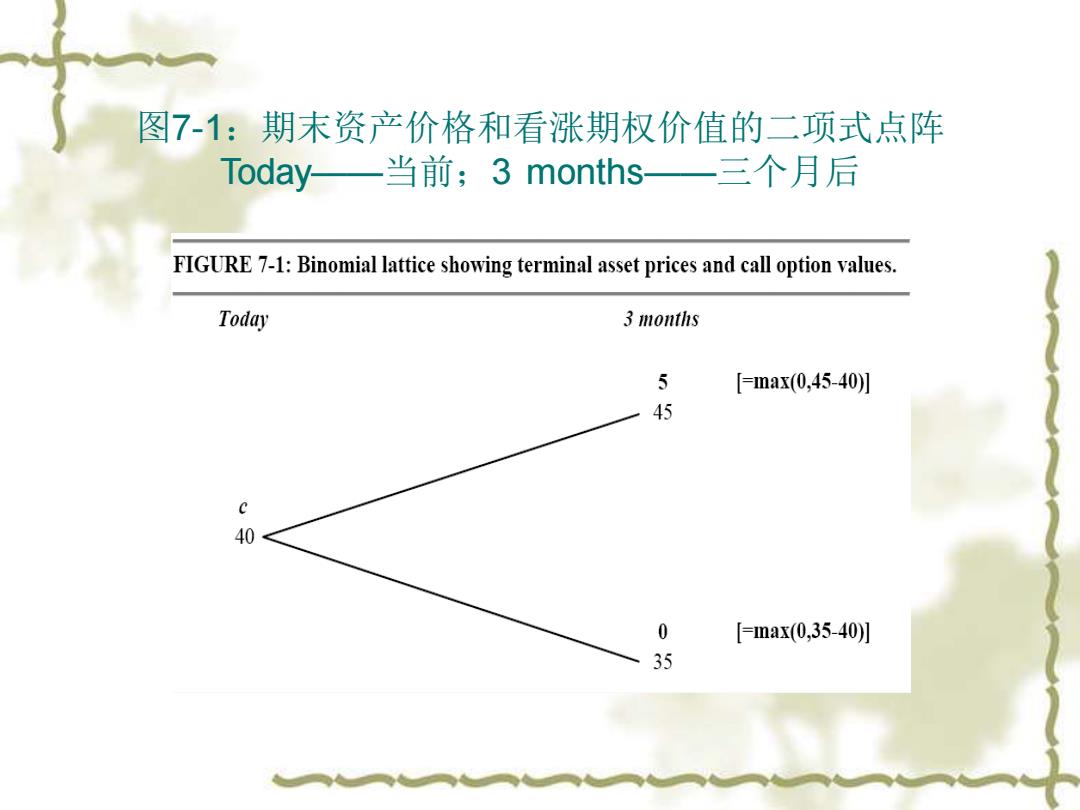
图7-1:期末资产价格和看涨期权价值的二项式点阵 Today-一当前;3 months-一三个月后 FIGURE 7-1:Binomial lattice showing terminal asset prices and call option values. Today 3 months 5 [=max(0,45-40)1 45 40 0 [=max(0,35-40)1 35
图7-1:期末资产价格和看涨期权价值的二项式点阵 Today——当前;3 months——三个月后