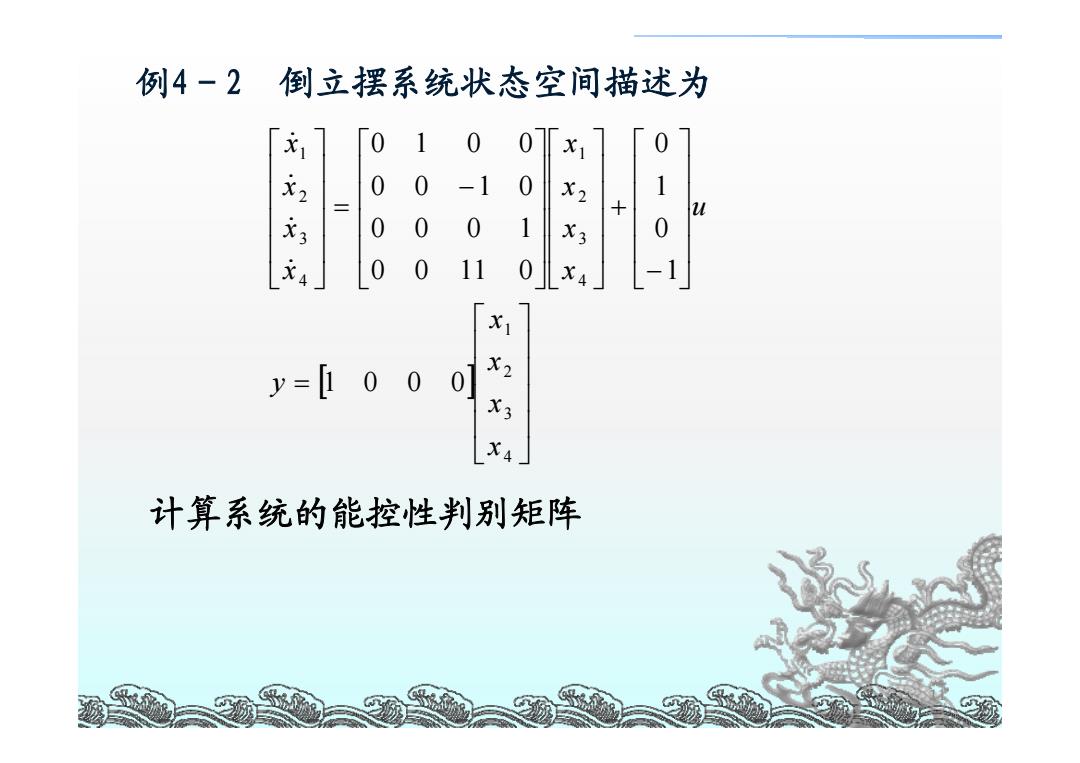
例4-2倒立摆系统状态空间描述为 戈 0 0 0 -1 0 X2 1 0 0 0 X3 4 0 0 11 0 X1 y=000] X3 X4 计算系统的能控性判别矩阵
11 例4-2 倒立摆系统状态空间描述为 计算系统的能控性判别矩阵 [ ] ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 4 3 2 1 4 3 2 1 4 3 2 1 1 0 0 0 1 0 1 0 0 0 11 0 0 0 0 1 0 0 1 0 0 1 0 0 x x x x y u x x x x x x x x & & & &

计算系统的能控性判别矩阵 0 1 1 0 1 0 U=B:AB:AB:A'B]= 0-1 0-11 -10-110 rankU =4=n 根据能控性秩判据,系统完全能控
12 计算系统的能控性判别矩阵 根据能控性秩判据,系统完全能控。 2 3 01 0 1 10 1 0 [ ] 0 1 0 11 1 0 11 0 U B AB A B A B ⎡ ⎤ ⎢ ⎥ = = ⎢ ⎥ ⎢ − − ⎥ ⎢ ⎥ ⎣− − ⎦ MM M rank n U = = 4

定理4-3[能控性PBH秩判据]线性连续定常系统 x=Ax+Bu 为完全能控的充分必要条件为 rank[I-A B=n i=1,...,n 或等价地 rank [sI-A B]=n,VsEC 式中,入,(i=1,…,n)为矩阵A的所有特征值, C为复数域。 证明:见教材P113
13 定理4-3[能控性PBH秩判据]线性连续定常系统 x& = Ax Bu + 为完全能控的充分必要条件为 rank n [ ] λiIAB − = i = 1,L, n rank s n [ ] IAB − = , ∀ s ∈ C ( i 1, , n ) λi = L A C 为矩阵 的所有特征值, 为复数域。 或等价地 式中, 证明:见教材 P113

例4-4设线性定常系统的状态方程为 0100] 0 00-10 10 尤= x+ W. n=4 000 1 0 1 0050 2 可直接导出 -10 00 1 0 S 1010 [sI-A B]= 0 0 -101 0 0 -5s-20
14 例4-4 设线性定常系统的状态方程为 01 0 0 0 1 00 10 1 0 , 4 00 0 1 0 1 00 5 0 20 x xu n ⎡ ⎤⎡ ⎤ ⎢ ⎥⎢ ⎥ − = += ⎢ ⎥⎢ ⎥ ⎢ ⎥⎢ ⎥ ⎢ ⎥⎢ ⎥ ⎣ ⎦⎣ ⎦ − & 可直接导出 [ ] 10 0 01 0 1 0 10 00 101 0 0 5 20 ⎡ − ⎤ ⎢ ⎥ − = ⎢ ⎥ ⎢ − ⎥ ⎢ ⎥ ⎣ − − ⎦ IAB s s s s s

求出A的特征值为: 21=入2=0,元3=5,入4=-V5 当5=1=入2=0时, 0-10001 001010 rank [sI-A B]=rank 000-1 =4 01 00-50-20 当s=元,=V5时 5-10 001 0 V51 010 rank[sI-A B]=rank 0√5 -101 00-5V5-2 0
15 求出A的特征值为: 0 λ1 = λ2 = 5 , , λ3 = λ4 = − 5 0 s = λ1 = λ2 = [ ] 0 10 0 01 00 1 0 10 4 00 0 101 0 0 5 0 20 rank s rank I AB ⎡ ⎤ − ⎢ ⎥ −= = ⎢ ⎥ ⎢ ⎥ − ⎢ ⎥ ⎣ ⎦ − − 当 时, s = λ3 = 5 [ ] 5 1 0 0 01 0 51 0 10 4 0 0 5 101 0 0 5 5 20 rank s rank I AB ⎡ ⎤ − ⎢ ⎥ ⎢ ⎥ −= = ⎢ ⎥ ⎢ ⎥ − ⎢ ⎥ ⎣ ⎦ − − 当 时