
1.2映射与变换 A->B 映射 A19 A x→y p(4)={p(x)x∈A}称为A,在p之下的像 (A)B p'(B)={x∈Ap(x)∈B,}称为B在p之下的逆像 o"(B)EA
1.2 映射与变换 映射 称为A1在φ之下的像 称为B1在φ之下的逆像 : A B x y → → A A 1 B B 1 1 1 (A x x A ) { ( ) } = 1 ( ) A B -1 1 1 (B x A x B ) { ( ) } = -1 1 ( ) B A

1.2映射与变换 ※p是满射<=>p(A)=B。 ※设A、B是两个有限集合,且A=B,p是A到 B的一个映射,则 p是单射<=>p是满射<=>p是双射
1.2 映射与变换 ※ φ是满射<=>φ(A)=B。 ※ 设A、B是两个有限集合,且 ,φ是A到 B的一个映射,则 φ是单射<=>φ是满射<=>φ是双射 A B =

1.2映射与变换 0:A→B 设 是双射 x->y 1:B→A 则 也是一个映射 y->x 且为双射,称p1为p的逆映射 双射才有逆映射,逆映射也为双射,且有 (p1)1=p
1.2 映射与变换 设 是双射 则 也是一个映射 且为双射,称φ-1为φ的逆映射 双射才有逆映射,逆映射也为双射,且有 (φ-1 ) -1=φ : A B x y → → -1 : B A y x → →

1.2映射与变换 设σ与都是A到B的映射,如果对任意x∈A, 都有σx)=(x),则称c与t相等,记作o=t
1.2 映射与变换 设σ与 都是A到B的映射,如果对任意 , 都有σ(x)=(x),则称σ与τ相等,记作σ=τ。 x A
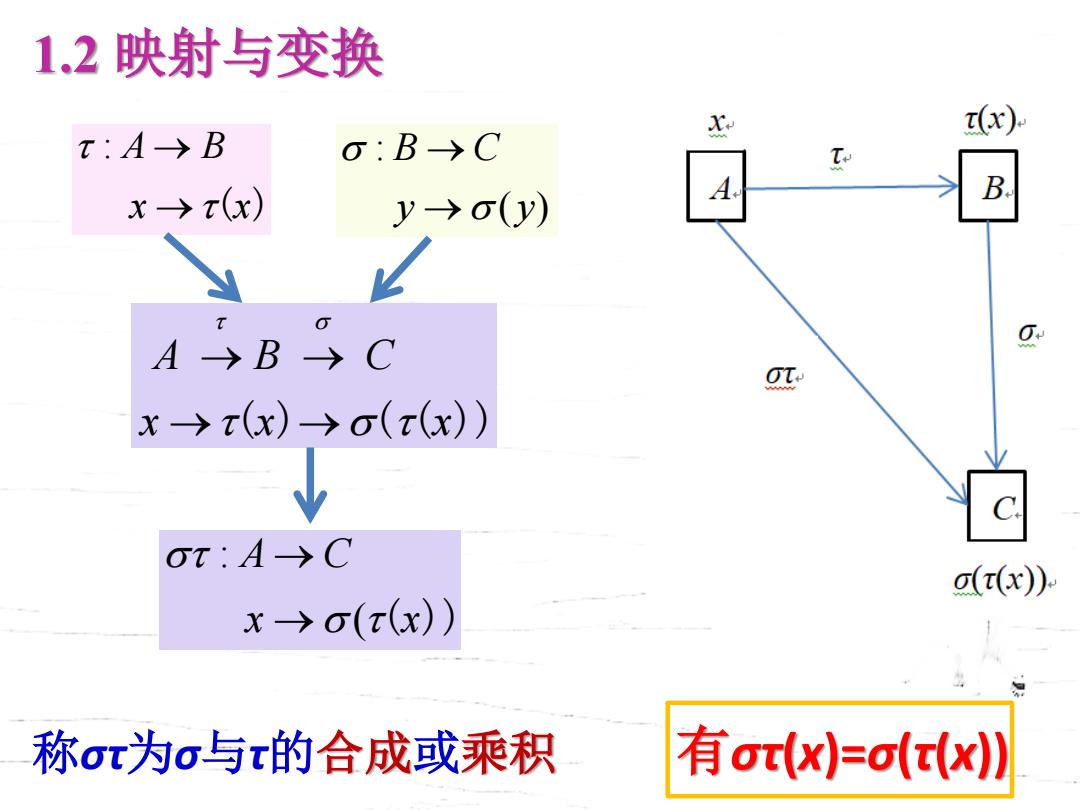
1.2映射与变换 X x) x:A→B o:B→C x->t(x) A B. y→o(y) A→BC g c x→(x)o(x(x) Ox:A→C a(r(x)) x→o((x)) 称oπ为o与r的合成或乘积 有ot(x=o(x)
1.2 映射与变换 称στ为σ与τ的合成或乘积 有στ(x)=σ(τ(x)) : A B x x → → ( ) : ( ) B C y y → → A B C x x x → → → → ( ) ( ( )) : ( A C x x → → ( ))