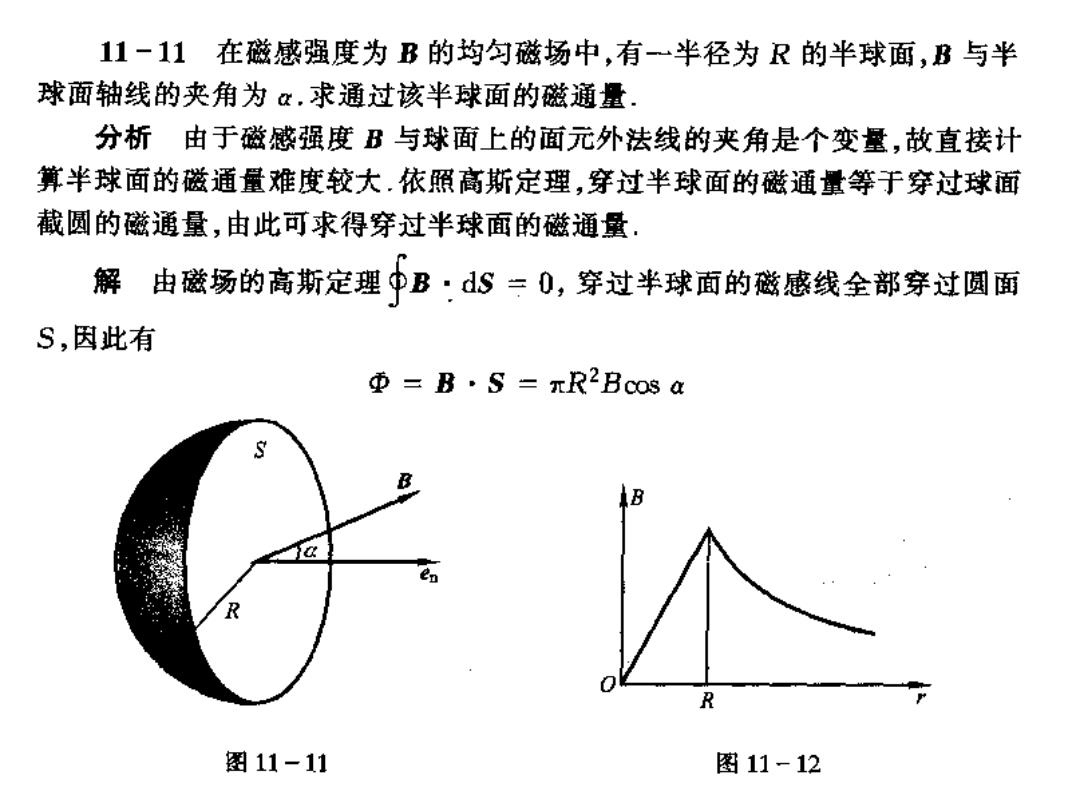
11-11在磁感强度为B的均匀磁场中,有一半径为R的半球面,B与半 球面轴线的夹角为α.求通过该半球面的磁通量. 分析由于磁感强度B与球面上的面元外法线的夹角是个变量,故直接计 算半球面的磁通量难度较大.依照高斯定理,穿过半球面的磁通量等于穿过球面 截圆的磁通量,由此可求得穿过半球面的磁通量 解由磁场的高斯定理巾B·dS三0,穿过半球面的磁感线全部穿过圆面 S,因此有 Φ=B·S=πR2Bco8a 图11-11 图11-12

11-12已知10m裸铜线允许通过50A电流而不会使导线过热.电流 在导线横截面上均匀分布.求:(1)导线内、外磁感强度的分布;(2)导线表面的 磁感强度。 分析可将导线视作长直圆柱体,电流沿轴向均匀流过导体,故其磁场必然 呈轴对称分布,即在与导线同轴的圆柱面上的各点,B大小相等,方向与电流成 右手螺旋关系为此,可利用安培环路定理,求出导线表面的磁感强度, 解(1)围绕轴线取同心圆为环路L,取其绕向与电流成右手螺旋关系,根 据安培环路定理,有 ΦB·dh=B2xr=4o1 R2,2s 在导线内r<R,∑I=L R2,因而 B=ltolr 2xR2 在导线外r>R,∑1=I,因而 B=器 磁感强度分布曲线如图11-12, (2)在导线表面磁感强度连续,由=50A,R=√S元=1.78×10~3m,得 品一 =5.6×103T
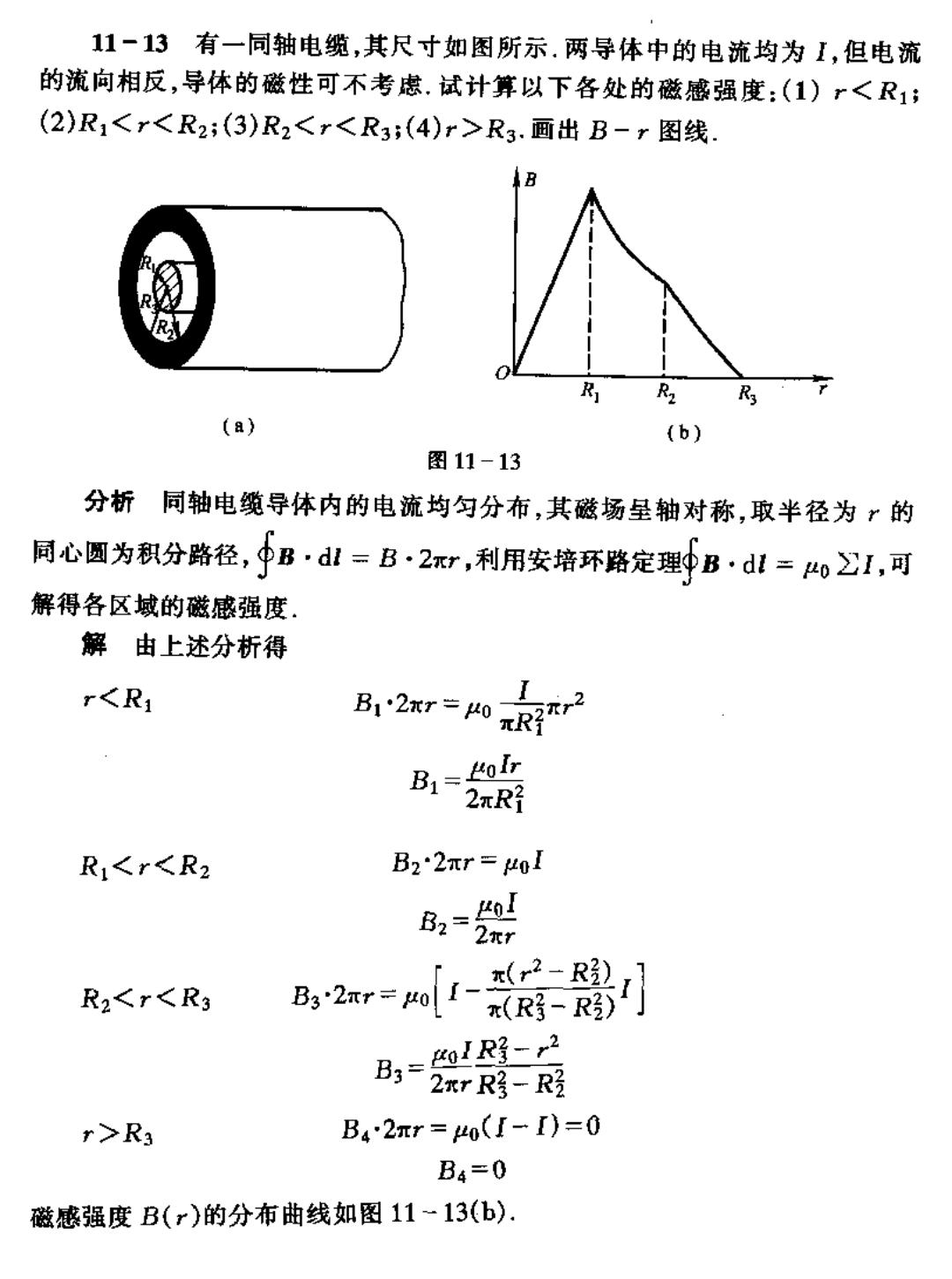
11-13有一同轴电缆,其尺寸如图所示.两导体中的电流均为1,但电流 的流向相反,导体的磁性可不考虑.试计算以下各处的磁感强度:(1)r<R1; (2)R1<r<R2;(3)R2<r<R3;(4)r>R3.画出B-r图线. (a) (b) 图11-13 分析同轴电缆导体内的电流均匀分布,其磁场呈轴对称,取半径为?的 同心圆为积分路径,中B·dl=B·2xr,利用安培环路定理砂B·dl=oI,可 解得各区域的磁感强度, 解由上述分析得 r<R B12mr-m元R72 B R1<r<R2 B22πr=01 器 R2<r<Rg a-器割 马影器 r>R3 B42mr=uo(I-I)=0 B4=0 磁感强度B(r)的分布曲线如图11-13(b)