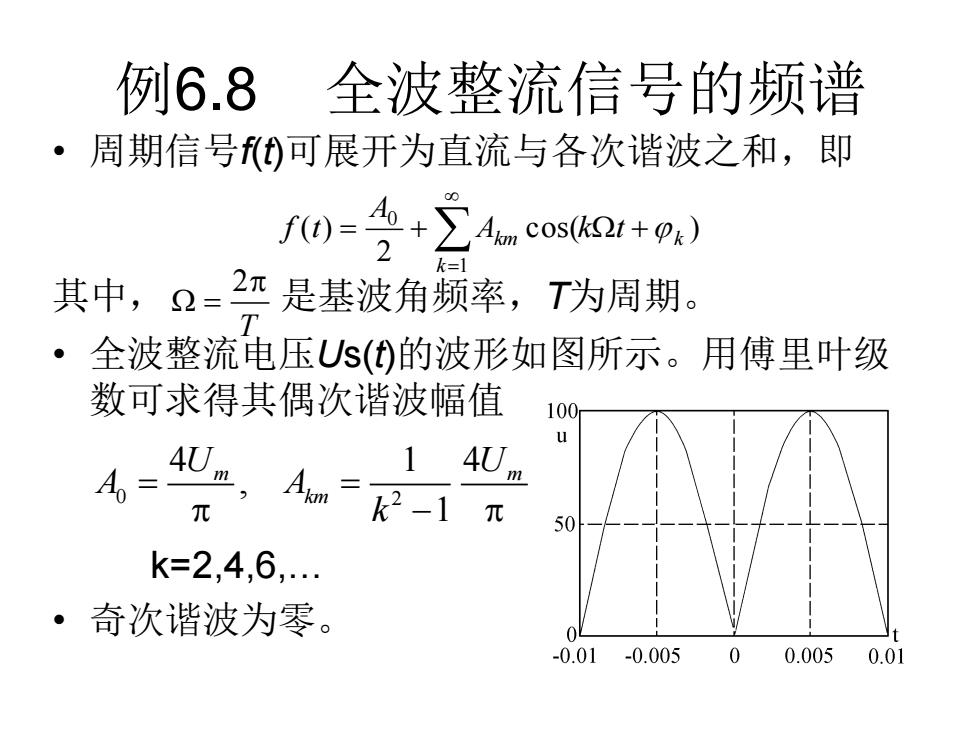
例6.8 全波整流信号的频谱 ·周期信号()可展开为直流与各次谐波之和,即 k=1 其中,Ω=2π是基波角频率,T为周期。 全波整流电压Us(①的波形如图所示。用傅里叶级 数可求得其偶次谐波幅值 100 u 4U. 1 A,= AUm 元 元 50 k=2,4,6,. ·奇次谐波为零。 -0.01-0.0050 0.0050.01
例6.8 全波整流信号的频谱 • 周期信号f(t)可展开为直流与各次谐波之和,即 其中, 是基波角频率,T为周期。 • 全波整流电压Us(t)的波形如图所示。用傅里叶级 数可求得其偶次谐波幅值 k=2,4,6,… • 奇次谐波为零。 cos( ) 2 ( ) 1 0 k k km A k t A f t = + + = T = 2 0 2 4 4 1 , 1 m m km U U A A k = = −

例6.8全波整流信号功率(续) ·信号每周期的有效值Us1可由数字积分求得 V.mF0dodo ·取前n项分量的功率求出的有效值Us2为 4领2】 ,的误差为6=。- U 用ε可以衡量所取谐波是否包含了原波形的主体
例6.8 全波整流信号功率(续) • 信号每周期的有效值Us1可由数字积分求得 • 取前n项分量的功率求出的有效值Us2为 用ε可以衡量所取谐波是否包含了原波形的主体。 sin d 1 sin d 2 1 sin d 1 0 2 2 0 2 0 2 s1 = = = m m T Um t t U U T U = − + = 3 1 2 2 2 s 4 1 1 2 1 2 4 1 2 n m n U U 1 2 1 2 s s s s U U U U − 的误差为 =
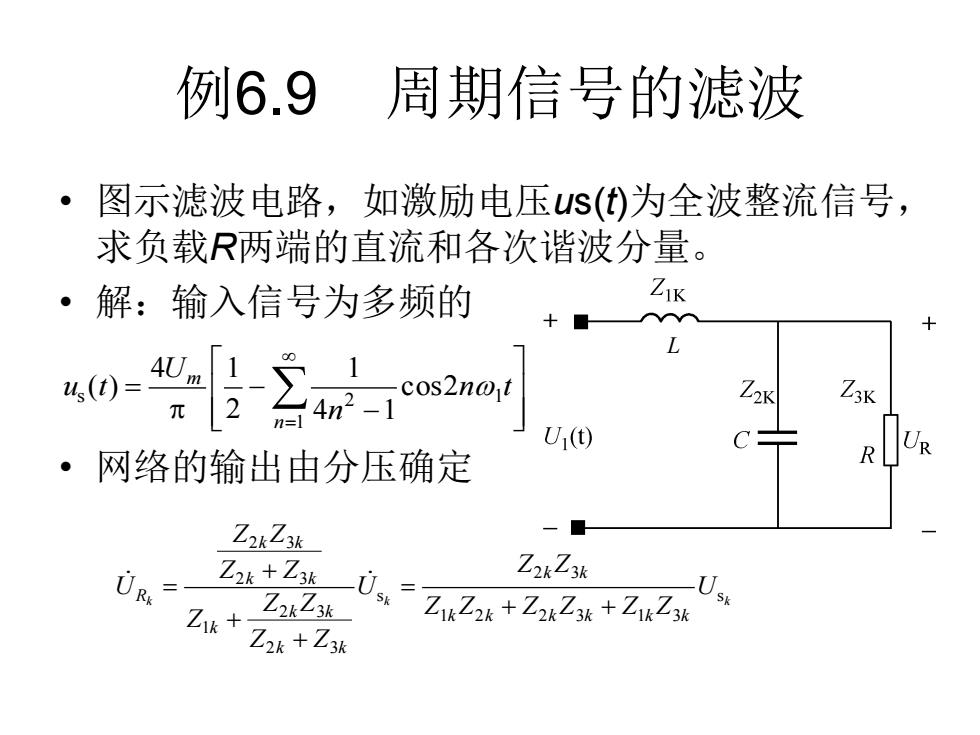
例6.9 周期信号的滤波 。 图示滤波电路,如激励电压uS()为全波整流信号, 求负载R两端的直流和各次谐波分量。 ·解:输入信号为多频的 Z3K U1() ·网络的输出由分压确定 Z2kZ3k 一■ Z2心,=Z2+22t+Z20 Z2kZ3k Zik+ Z2kZ3k Z2k+Z3k
例6.9 周期信号的滤波 • 图示滤波电路,如激励电压us(t)为全波整流信号, 求负载R两端的直流和各次谐波分量。 • 解:输入信号为多频的 • 网络的输出由分压确定 L k k k U Z Z Z Z Z Z Z Z U Z Z Z Z Z Z Z Z Z U k k k k k k k k k k k k k k k k k R s 1 2 2 3 1 3 2 3 s 2 3 2 3 1 2 3 2 3 + + = + + + = − − = =1 s 2 2 1 cos 4 1 1 2 4 1 ( ) n m n t n U u t

例6.9 周期信号的滤波(续) ·信号幅度随频率而变 1 0FR2-14n2 (k=2n,n=1,2,3,) ·元件和系统函数都是频率的函数 jkot.-pnol,Za--jgoc--jzmcZ-R ·因此输出电压为 COLR-ImC ·由此式可求得UR的各次谐波
例6.9 周期信号的滤波(续) • 信号幅度随频率而变 • 元件和系统函数都是频率的函数 • 因此输出电压为 • 由此式可求得UR的各次谐波。 ( 2 1, 2 , 3,) 4 1 1 1 1 s 2 2 = = − = − = k n n k n U k , 1 1 1 2 3 1 1 1 1 j j2 , j j , 2 Z k L n L Z Z R k k k k C n C = = = − = − = + − − = k C R k LR C L U k C R U k Rk 1 1 s 1 j j

例6.10调幅信号通过带通滤波器 ·已知带通滤波器的系统函数为 U2(S) 2s H(s)= U1(s)(s+1)2+1002 激励电压u1()=(1+c0st)c0s(100t) 求(1)带通滤器的频率响应; (2)输出的稳态响应u2(⑤并画出波形。 解:将激励信号u1(⑤展开为傅立叶级数 4(0=2cos990+cos100)+2cos(1010)
例6.10 调幅信号通过带通滤波器 • 已知带通滤波器的系统函数为 激励电压u1(t) = (1+cost ) cos (100t) 求(1)带通滤器的频率响应; (2)输出的稳态响应u2(t)并画出波形。 解:将激励信号u1(t)展开为傅立叶级数 2 2 1 2 ( 1) 100 2 ( ) ( ) ( ) + + = = s s U s U s H s cos(101 ) 2 1 cos(99 ) cos(100 ) 2 1 ( ) 1 u t = t + t + t