
高价导数 一、高阶导数的定义 问题:变速直线运动的加速度 设s=f(t),则瞬时速度为y(t)=f'(t) .加速度是速度v对时间t的变化率 .a(t)=v'(t)=[f'(t)'. 定义如果函数f(x)的导数f'(x)在点x处可导,即 (f(x)y'=lim I(x+Ax)-f(x) △x-→0 △x 存在,则称(f'(x)'为函数f(x)在点x处的二阶导数
高阶导数 一、高阶导数的定义 问题:变速直线运动的加速度. 设 s = f (t), 则瞬时速度为v(t) = f (t) 加速度a是速度v对时间t的变化率 a(t) = v(t) = [ f (t)] . 定义 , ( ( )) ( ) . ( ) ( ) ( ( )) lim ( ) ( ) , 0 存 在 则 称 为函数 在 点 处的二阶导数 如果函数 的导数 在 点 处可导 即 f x f x x x f x x f x f x f x f x x x + − = →

记作∫xy八,或4f田 2 2 二阶导数的导数称为三阶导数,f"x,y”, 3 三阶导数的导数称为四阶导数,f(x),y d"y dx' 一般地,函数f(x)的n-1阶导数的导数称为 函数f(x)的n阶导数,记作 f%,或4f dx" 二阶和二阶以上的导数统称为高阶导数, 相应地,f(x)称为零阶导数;f'(x)称为一阶导数
记作 . ( ) ( ), , 2 2 2 2 dx d f x dx d y f x y 或 二阶导数的导数称为三阶导数, ( ), , . 3 3 dx d y f x y 三阶导数的导数称为四阶导数, ( ), , . 4 4 (4) (4) dx d y f x y 函 数 的 阶导数 记 作 一般地 函 数 的 阶导数的导数称为 ( ) , , ( ) 1 f x n f x n − . ( ) ( ), , ( ) ( ) n n n n n n dx d f x dx d y f x y 或 二阶和二阶以上的导数统称为高阶导数. 相应地, f (x)称为零阶导数; f (x)称为一阶导数

二、高阶导数求法举例 1.直接法:由高阶导数的定义逐步求高阶导数. 例1设y=arctanx,求f"(0),f"(0). 解 -a+y 0-0+w-2
二、 高阶导数求法举例 1.直接法:由高阶导数的定义逐步求高阶导数. 例1 设 y = arctan x,求f (0), f (0). 解 2 1 1 x y + = ) 1 1 ( 2 + = x y 2 2 (1 ) 2 x x + − = ) (1 ) 2 ( 2 2 + − = x x y 2 3 2 (1 ) 2(3 1) x x + − = 2 2 0 (1 ) 2 (0) = + − = x x x f = 0; 2 3 0 2 (1 ) 2(3 1) (0) = + − = x x x f = −2
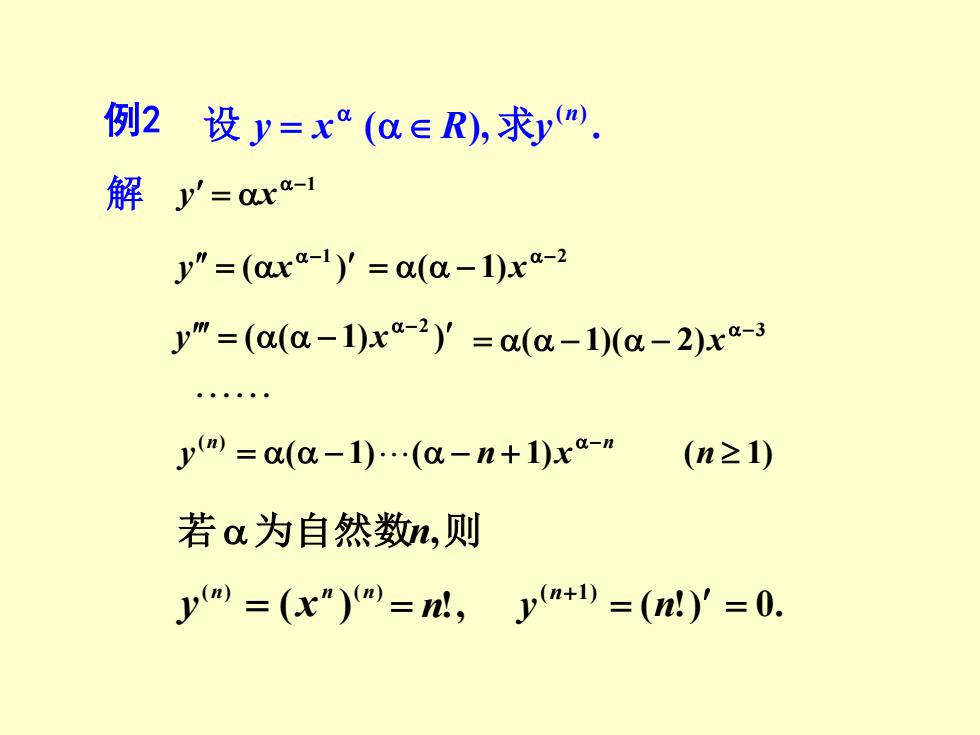
例2设y=xa(a∈R),求ym. 解y'=0xa-1 Jy"=(0xa-1)y=0(a-1)xa-2 y"=((a-1)xa-2)y'=c(a-10(a-2)xa-3 yw=0(a-1).(a-n+1)xa-" (n≥1) 若o为自然数n,则 yw=(x")=,y+=(n)y=0
例 2 ( ), . (n) 设 y = x R 求y 解 −1 y = x( ) 1 = − y x 2 ( 1) − = − x ( ( 1) ) 2 = − − y x 3 ( 1)( 2) − = − − x ( 1) ( 1) ( 1) ( ) = − − + − y n x n n n 若为自然数n,则 ( ) ( ) ( ) n n n y = x = n!, ( !) ( 1) = + y n n = 0
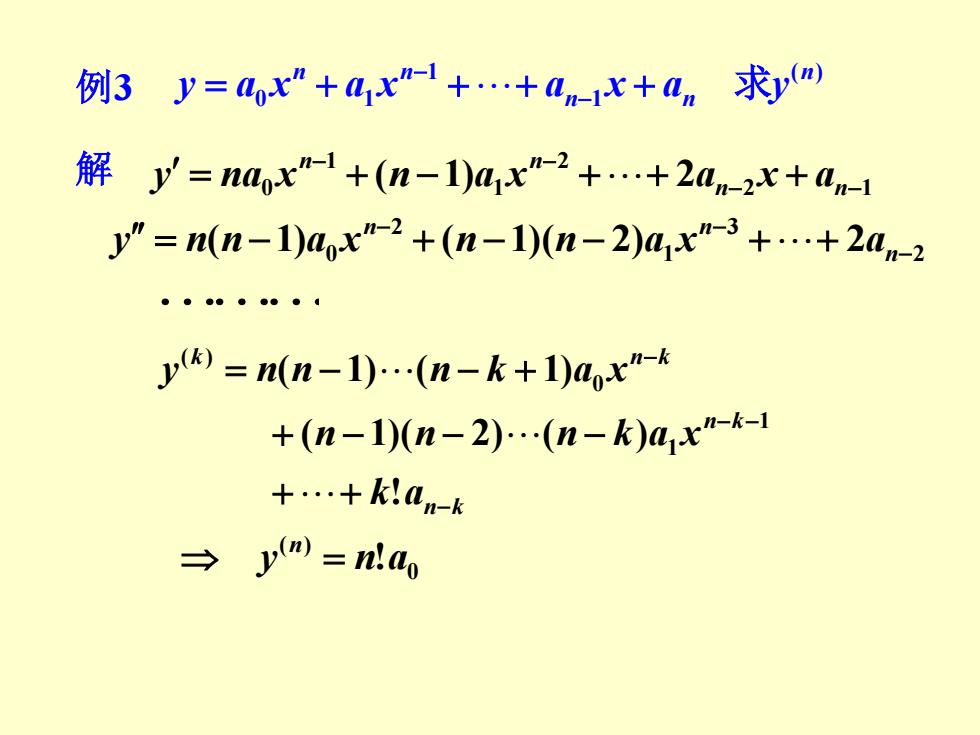
例3y=4x"+a1x"-+.+0n-1x+an求ym 解y=nax1+(n-1)41x-2++2an-2x+-1 y"=n(n-1)a.x"-2+(n-10(n-2)ax”-3+.+2an-2 y=n(n-1).(n-k+1)ax"- +(n-10(n-2).(n-k)axr-1 +.+k:am-k →ym=n!ao
例 3 ( ) 1 1 0 1 n n n n n y = a x + a x + + a x + a 求y − − 解 2 1 2 1 1 0 ( 1) 2 − − − − = + − + + n + n n n y na x n a x a x a 2 3 1 2 ( 1) 0 ( 1)( 2) 2 − − − = − + − − + + n n n y n n a x n n a x a n k n k k n k k a n n n k a x y n n n k a x − − − − + + + − − − = − − + ! ( 1)( 2) ( ) ( 1) ( 1) 1 1 0 ( ) 0 ( ) y n!a n =